Построение синусоиды в excel

График линейной функции

Линейная функция задается уравнением . График линейной функций представляет собой прямую. Для того, чтобы построить прямую достаточно знать две точки.

Пример 1

Построить график функции . Найдем две точки. В качестве одной из точек выгодно выбрать ноль.

Если , то

Берем еще какую-нибудь точку, например, 1.

Если , то

При оформлении заданий координаты точек обычно сводятся в таблицу:

 
А сами значения рассчитываются устно или на черновике, калькуляторе.

Две точки найдены, выполним чертеж:

При оформлении чертежа всегда подписываем графики.

Не лишним будет вспомнить частные случаи линейной функции:

Обратите внимание, как я расположил подписи, подписи не должны допускать разночтений при изучении чертежа. В данном случае крайне нежелательно было поставить подпись рядом с точкой пересечения прямых  ,  или справа внизу между графиками

1) Линейная функция вида  () называется прямой пропорциональностью. Например, . График прямой пропорциональности всегда проходит через начало координат. Таким образом, построение прямой упрощается – достаточно найти всего одну точку.

2) Уравнение вида  задает прямую, параллельную оси , в частности, сама ось  задается уравнением . График функции строится сразу, без нахождения всяких точек. То есть, запись  следует понимать так: «игрек всегда равен –4, при любом значении икс».

3) Уравнение вида  задает прямую, параллельную оси , в частности, сама ось  задается уравнением . График функции также строится сразу. Запись  следует понимать так: «икс всегда, при любом значении игрек, равен 1».

Некоторые спросят, ну зачем вспоминать 6 класс?! Так-то оно, может и так, только за годы практики я встретил добрый десяток студентов, которых ставила в тупик задача построения графика вроде  или .

Построение прямой – самое распространенное действие при выполнении чертежей.

Прямая линия детально рассматривается в курсе аналитической геометрии, и желающие могут обратиться к статье Уравнение прямой на плоскости.

Построение синусоиды в excel

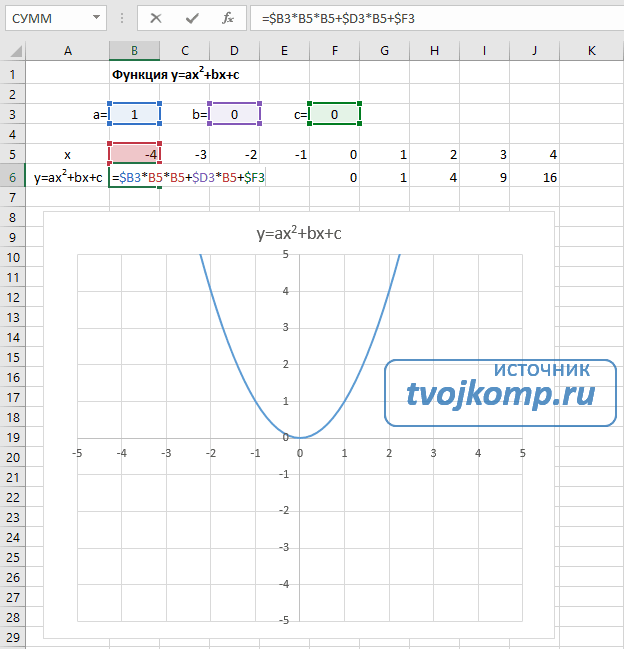
Как построить график синусоиды в Excel.

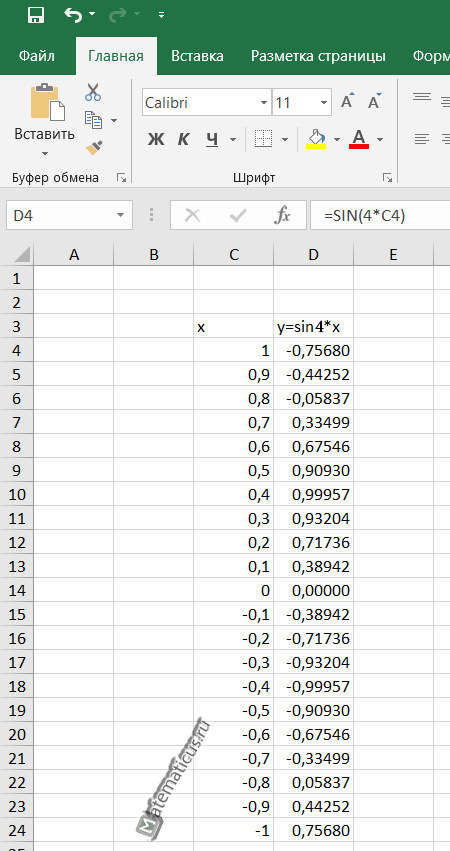
Допустим имеется функция синусоиды, заданной уравнением y=sin4*x. Формула в Excel имеет вид:

=SIN(4*C4)

Требуется построить график функции.

Функция в данном случае непрерывная, поэтому по оси x ограничим интервалом от 1 до -1, шаг возьмём 0,1.

В итоги у нас должна получится таблица вида:

Переходим на вкладку Вставка -> Точечная с гладкими кривыми и маркерами.

Появится область графика, кликаем на белую область правым указателем мыши, выскакивает меню, далее Выбрать данные, появляется окно Выбора источника данных, выбираем весь диапазон данных нашей синусоиды в ячейках, затем Ок.

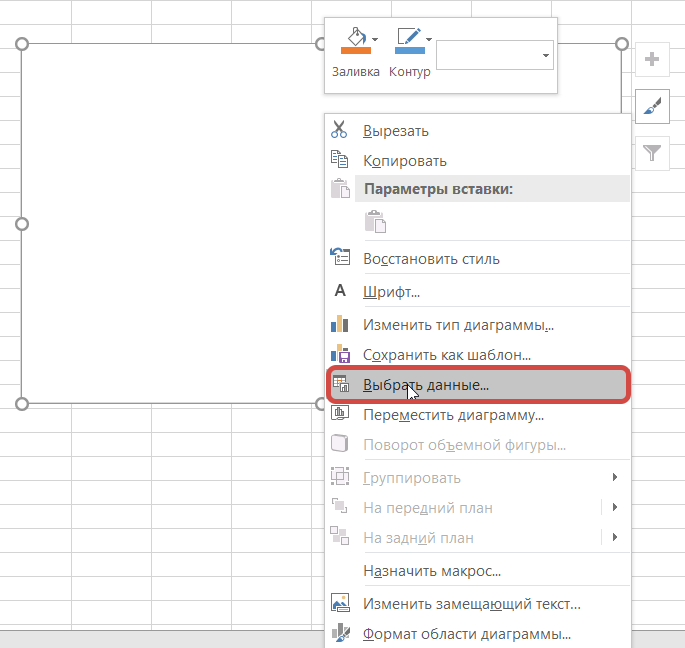
В итоги у нас получается график вида.

Также вид графика тоже можно настроить через конструктор и дополнительные инструменты.

трюки • приёмы • решения

Использование диаграмм Excel — хороший способ отображения графиков математических и тригонометрических функций. В этой статье описываются два метода построения графика функции: с одной переменной с помощью точечной диаграммы и с двумя переменными с помощью 3D-диаграммы.

Построение графиков математических функций с одной переменной

Точечная диаграмма (известная как диаграмма XY в предыдущих версиях Excel) отображает точку (маркер) для каждой пары значений. Например, на рис. 140.1 показан график функции SIN. На диаграмму наносятся рассчитанные значения у для значений х (в радианах) от -5 до 5 с инкрементом (приращением) 0,5. Каждая пара значений х и у выступает в качестве точки данных в диаграмме, и эти точки связаны линиями.

Рис. 140.1. Диаграмма представляет собой график функции SIN(x)

Функция выражается в таком виде: у = SIN(x) .

Соответствующая формула в ячейке В2 (которая копируется в ячейки, расположенные ниже) будет следующей: =SIN(A2) .

Чтобы создать эту диаграмму, выполните следующие действия.

1. Выделите диапазон А1:В22 .
2. Выберите Вставка ► Диаграммы ► Точечная ► Точечная с прямыми отрезками и маркерами.
3. Выберите макет диаграммы, который вам нравится, а затем настройте его.

Измените значения в столбце А для построения графика функции при различных значениях х. И, конечно, вы можете использовать любую формулу с одной переменной в столбце В. Вот несколько примеров, которые приводят к построению интересных графиков: =SIN(ПИ()*A2)*(ПИ()*A2) =SIN(A2)/A2 =SIN(A2^3)*COS(A2^2) =НОРМ.РАСП(A2;0;1;ЛОЖЬ)

Чтобы получить более точную диаграмму, увеличьте количество значений для построения графика и сделайте приращение в столбце А меньше.

Вы можете использовать онлайн наш файл примера графиков математических функций с одной переменной, расположенной в Excel Web Apps при помощи Skydrive, и внести свои данные (изменения не будут сохраняться) или скачать себе на компьютер, для чего необходимо кликнуть по иконке Excel в правом нижнем углу. Это бесплатно

Построение графиков математических функций с двумя переменными

Вы также можете строить графики функций, которые используют две переменные. Например, следующая функция рассчитывает z для различных значений двух переменных (х и у): =SIN($A2)*COS($B1)

На рис. 140.2 приведена поверхностная диаграмма, которая рассчитывает значение z для 21 значения х в диапазоне от -3 до 0 и для 21 значения у в диапазоне от 2 до 5. Для х и у используется приращение 0,15.

Рис. 140.2. Использование трехмерной поверхностной диаграммы для построения графика функции с двумя переменными

Значения х находятся в диапазоне А2:А22 , а значения у — в диапазоне B1:V1 .

Формула в ячейке В2 копируется в другие ячейки таблицы и имеет следующий вид: =SIN($A2)*C0S(B$1) .

Чтобы создать диаграмму, выполните приведенные ниже действия.

1. Выделите диапазон A1:V22 .
2. Выберите Вставка ► Диаграммы ► Другие ► Поверхность.
3. Выберите макет диаграммы, который вам нравится, а затем настройте его.

Пока значения х и у имеют равные приращения, вы можете задавать любую формулу с двумя переменными. Вам, возможно, потребуется настроить начальные значения и значение приращения для х и у. Для увеличения сглаживания используйте больше значений х и у при меньшем приращении. Вот другие формулы, которые вы можете попробовать: =SIN(КОРЕНЬ($A2^2+B$1^2)) =SIN($A2)*COS($A2*B$1) =COS($A2*B$1)

Функция SIN в Excel используется для вычисления синуса угла, заданного в радианах, и возвращает соответствующее значение.

Функция SINH в Excel возвращает значение гиперболического синуса заданного вещественного числа.

Функция COS в Excel вычисляет косинус угла, заданного в радианах, и возвращает соответствующее значение.

Функция COSH возвращает значение гиперболического косинуса заданного вещественного числа.

Таблица синусов и косинусов в Excel

Пример 2. Ранее в учебных заведениях широко использовались справочники тригонометрических функций. Как можно создать свой простой справочник с помощью Excel для косинусов углов от 0 до 90?

Заполним столбцы значениями углов в градусах:

Для заполнения используем функцию COS как формулу массива. Пример заполнения первого столбца:

=COS(РАДИАНЫ(A2:A16))

Вычислим значения для всех значений углов. Полученный результат:

Примечание: известно, что cos(90°)=0, однако функция РАДИАНЫ(90) определяет значение радианов угла с некоторой погрешностью, поэтому для угла 90° было получено отличное от нуля значение.

Аналогичным способом создадим таблицу синусов в Excel:

Обратные тригонометрические функции

Такие функции выполняют обратный расчет по отношению к перечисленным выше:

• Арккосинус – это угол, который образуют прилежащий катет и гипотенуза с определенным косинусом. Чтобы посчитать эту величину, используйте функцию ACOS(Значение косинуса) .
• Арксинус – угол между противолежащим катетом и гипотенузой с определенным синусом, вычисляется так: ASIN(Значение синуса) .
• Арктангенс – угол между противолежащим и прилежащим катетами для заданного тангенса: ATAN(Значение тангенса) .
• Арккотангенс – угол, для которого справедливо заданное значение котангенса: ACOT(Значение котангенса).

Все перечисленные функции вернут угол в радианах. Естественно, для перевода его в градусы, используем функцию ГРАДУСЫ .

Знание и умелое применение перечисленных функций, конечно, не сделает Вас богом в тригонометрии, но все же позволит выполнить сложные расчеты, «стоимость» которых часто довольно высока. Научитесь комбинировать их с другими функциями, построением графиков, чтобы получить максимальный эффект от полученных знаний.

Это все о тригонометрических функциях, спасибо, что читаете мой блог и развиваетесь в своих знаниях. Следующую статью я напишу об округлении чисел и очень Вам рекомендую ее не пропустить!

Рубрика «Вопросы и ответы»

Первый раз, изучая синусы, я упустил несколько вещей:

Синус вообще-то 1-мерный.

Синус движется в одном измерении. Правда. Мы часто рисуем синус, изменяющийся во времени, а иногда и «предмет», описывающий своим движением синус, тоже куда-то движется, но это уже опционально! Скачок в одном направлении — вполне себе полноценная волна синусоиды.

Окружности — это пример синусных волн.

Окружности и квадраты — это комбинации базовых элементов (синусов и прямых отрезков). Но окружности не являются основой синусоиды, как и квадрат не является составной частью прямой.

Что показывают значения синуса?

Синус принимает значения от -1 до 1. Он начинается с 0, возрастает до 1.0 (максимум), падает до -1.0 (минимум) и снова возвращается в нейтральную точку, к нулю. Я также вижу синус как процент от 100% (полный вперёд!) до -100% (полный обратный ход).

Что означает вводное значение ‘x’ в функции sin(x)?

Каверзный вопрос. Поскольку это цикл и х — вводный параметр, он означает, как далеко мы прошли по окружности.

Рассмотрим пример с линиями:

• Мы бродим по квадрату. За 10 секунд мы проходим каждую сторону.
• Спустя 1 секунду, вы прошли 10% от одной стороны
• Спустя 5 секунд, вы прошли одну сторону на 50%
• Через 10 секунд вы пройдете всю сторону.

В линейном движении есть парочка сюрпризов. Рассмотрим теперь синус (сфокусируемся на цикле «от 0 до максимума»):

• Мы путешествуем по синусоиде, стартуя с 0 (нейтральная точка) до 1.0 (максимум). И на этот путь у нас ушло 10 секунд.
• Спустя 5 секунд мы…прошли 70%! Синус очень быстрый на старте, и потихоньку замедляется к вершине. Так что большую часть пути мы пройдем за первые 5 секунд.
• И еще 5 секунд нам потребуется на то, чтобы пройти с 70% до 100% пути. А отрезок с 98% до 100% занимает почти целую секунду!

Несмотря на высокую начальную скорость, синус замедляет свой рост, так что мы очень плавно касаемся точки максимума и разворачиваемся назад. Эта плавность и делает синус синусом.

Если вам очень интересны подробности, нажмите «show stats» в симуляторе. Вы увидите процент выполнения полного цикла, мини-цикла (с 0 до 1.0) и текущее значение. Остановите движение (кнопка Stop), попереключайтесь между линейным и синусоидальным движением, чтобы сравнить значения.

Маленькая проверка: Что будет дальше, 10% линейного цикла или 10% синусного? Правильный ответ — синусного.

Помните, в самом начале синус максимально ускорен. Ко времени достижения 50% цикла, синус движется со средней скоростью линейного цикла и, более того, замедляется (пока не достигнет максимума и не развернется).

Так что x — это «количество вашего цикла». Какого цикла?

Зависит от контекста.

• Базовый вариант: ‘x’ — это градусы, и полный цикл состоит из 360 градусов
• Продвинутый вариант: ‘x’ — это радианы (они более натуральные!) и полный цикл составляет полный проход по единичной окружности (2*π радиан)

Поэкспериментируйте со значением х здесь:

Но опять же, циклы зависят от окружностей! Можем ли мы как-то вырваться из-под их тирании?

7 Графики синуса и косинуса

Построим график функции . При этом нам опять пригодятся
часы из разд. 2.1.

Если , то, очевидно, . Когда возрастает от 0 до
, число возрастает от 0 до 1 (представьте себе,
как меняется ордината конца стрелки на наших фирменных часах).
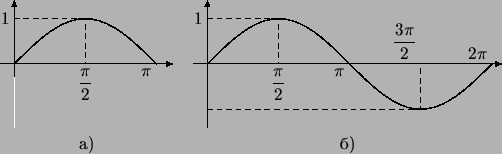
Участок графика для от 0 до изображен на
рис. .
При

Чем ближе к , тем более полого идет наша кривая. Это
происходит потому, что проекция конца стрелки на ось
ординат, колеблясь по отрезку , быстрее всего
движется в середине отрезка и замедляется у его краев: мы
это уже обсуждали в разд. 2.1.

симметричны относительно прямой

Задача 7.1  
Запишите уравнение прямой, касающейся графика функции
в точке с координатами .

Кривая на рис б
центрально симметрична относительно точки
с координатами ; это следует из другой формулы
приведения:
(рис. б).

После того, как у нас есть участок графика функции для

, весь график строится уже просто. В самом деле,
когда конец стрелки прошел путь , стрелка вернулась
в исходное положение; при дальнейшем движении все будет
повторяться. Значит, график будет состоять из таких же кусков,
как на рис б. Окончательно график функции
выглядит так, как на рис. .

Теперь построим график функции . Можно было бы строить его так же, как
мы строили график синуса. Мы, однако, изберем другой путь,
который позволит использовать уже имеющуюся у нас информацию.

Именно, воспользуемся формулой приведения
. Эту формулу можно понимать так: функция
принимает те же значения, что и функция , но на
раньше. Например, функция принимает значение 1 при
, а функция
принимает это же
значение уже при . На графике это означает следующее: для
каждой точки графика есть точка графика ,
у которой ордината та же, а абсцисса на меньше
(рис. ).

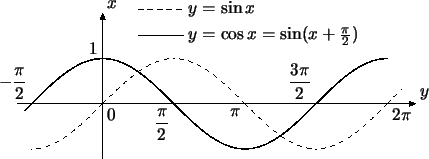сдвинуть график

Итак, мы выяснили, что график косинуса получается преобразованием
(сдвигом) из графика синуса. Случаи, когда график одной функции
можно получить преобразованием из графика другой функции,
интересны и сами по себе, поэтому скажем о них несколько слов.

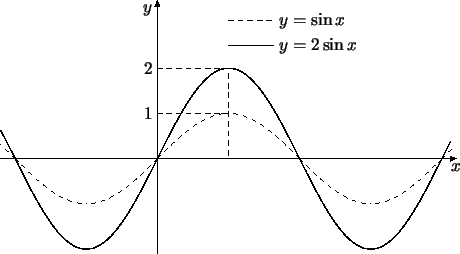
Как, например, будет выглядеть график функции ? Ясно,
что ординаты точек этого графика получаются из ординат
соответствующих точек графика умножением на 2, так что
наш график изобразится сплошной кривой на рис. . Можно
сказать, что график получается из графика растяжением в два раза вдоль оси
ординат.

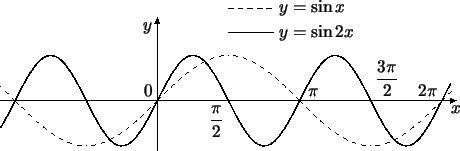сжатием в 2 раза к оси ординат.

Попробуем еще построить график функции 
.
Понятно, что он должен получаться каким-то преобразованием из
графика . На первый взгляд может показаться, что это
преобразование — сдвиг влево на вдоль оси абсцисс, по
аналогии с тем, что изображено на рис. . Однако, если
бы это было так, то вышло бы, например, что функция

принимает значение 1 при

, что не соответствует действительности
(проверьте!). Правильно рассуждать так:
, так что функция
принимает те
же значения, что и функция , но на раньше. Так
что сдвиг влево — не на
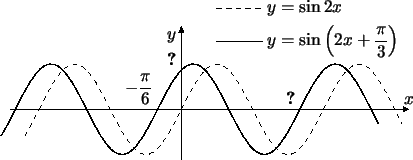
, а на (рис. ).

Кривые, являющиеся графиками функций
, где ,
, называются синусоидами. Заметим, что кривой
«косинусоида» вводить не надо: как мы видели, график косинуса
— это та же кривая, что и график
синуса, только иначе
расположенная относительно осей координат.

Задача 7.2  
Каковы координаты точек, помеченных на
рис.  вопросительными знаками?

Задача 7.3  
Возьмите свечу, тонкий лист бумаги и острый нож. Намотайте лист
бумаги на свечу в несколько слоев и аккуратно разрежьте эту свечу
вместе с бумагой наискосок ножом. Теперь разверните бумагу. Вы
увидите, что она оказалась разрезанной по волнистой линии.
Докажите, что эта волнистая линия является синусоидой.

Задача 7.4  
Постройте графики функций:

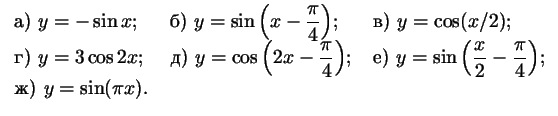
Замечание. Если вы строите графики
тригонометрических функций на клетчатой бумаге, удобно выбрать
немного разные масштабы по осям, с тем чтобы на оси абсцисс
числу  соответствовало целое число клеточек. Например, часто
выбирают такой масштаб: по оси ординат отрезок длины 1 занимает
две клеточки, по оси абсцисс отрезок длины занимает 6
клеточек.

Задача 7.5  
Постройте графики функций:
а)
;
б)
.

Посмотрим, как выглядят на графиках уже известные нам решения
уравнений и . Эти решения являются
абсциссами точек пересечения горизонтальной прямой
с графиком функций (соответственно ). На
рис. , хорошо видны две серии решений,
получающихся при .

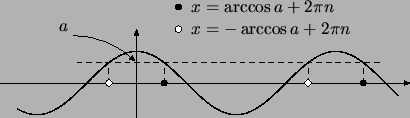По графикам синуса и косинуса видно, на каких промежутках эти
функции возрастают, а на каких убывают. Ясно, например, что
функция возрастает на отрезках
,

,
,…- одним словом, на
всех отрезках
, где
,
и убывает на всех отрезках
, где

.

Задача 7.6  
На каких отрезках возрастает и на каких убывает
функция ?

Задача 7.7  
Сравните числа:

Задача 7.8  
Расположите в порядке возрастания:
, , , , , .

        Написать комментарий

Особенности использования тригонометрических функций в Excel

Синтаксис функции SIN:

Синтаксис функции SINH:

Синтаксис функции COS:

Синтаксис функции COSH:

Каждая из приведенных выше функций принимает единственный аргумент число, который характеризует угол, заданный в радианах (для SIN и COS) или любое значение из диапазона вещественных чисел, для которого требуется определить гиперболические синус или косинус (для SINH и COSH соответственно).

1. Если в качестве аргумента любой из рассматриваемых функций были переданы текстовые данные, которые не могут быть преобразованы в числовое значение, результатом выполнения функций будет код ошибки #ЗНАЧ!. Например, функция =SIN(“1”) вернет результат 0,8415, поскольку Excel выполняет преобразование данных там, где это возможно.
2. В качестве аргументов рассматриваемых функций могут быть переданы логические значения ИСТИНА и ЛОЖЬ, которые будут интерпретированы как числовые значения 1 и 0 соответственно.
3. Все рассматриваемые функции могут быть использованы в качестве формул массива.

1. Синус гиперболический рассчитывается по формуле: sinh(x)=0,5*(ex-e-x).
2. Формула расчета косинуса гиперболического имеет вид: cosh(x)=0,5*( ex+e-x).
3. При расчетах синусов и косинусов углов с использованием формул SIN и COS необходимо использовать радианные меры углов. Если угол указан в градусах, для перевода в радианную меру угла можно использовать два способа:

• Функция РАДИАНЫ (например, =SIN(РАДИАНЫ(30)) вернет результат 0,5;
• Выражение ПИ()*угол_в_градусах/180.

Примеры использования функций SIN, SINH, COS и COSH в Excel

Пример 1. Путешественник движется вверх на гору с уклоном в 17°. Скорость движения постоянная и составляет 4 км/ч. Определить, на какой высоте относительно начальной точке отсчета он окажется спустя 3 часа.

Таблица данных:

Для решения используем формулу:

=B2*B3*SIN(РАДИАНЫ(B1))

Описание аргументов:

• B2*B3 – произведение скорости на время пути, результатом которого является пройденное расстояние (гипотенуза прямоугольного треугольника);
• SIN(РАДИАНЫ(B1)) – синус угла уклона, выраженного в радианах с помощью функции РАДИАНЫ.

В результате расчетов мы получили величину малого катета прямоугольного треугольника, который характеризует высоту подъема путешественника.

Свойства и доказательства

К главным свойствам синусоиды относятся область значений (включая нуль) и определений, чётность/нечётность, периодичность, точки пересечения с осью координат, промежуточности постоянства, убывания и возрастания, минимум и максимум. При пересечении графика функции (ГФ) с осью Ох результат равняется нулю. Под значением синуса подразумевается ордината соответствующей точки единичной окружности.

Значения ординаты единичной окружности (ЕД) расположены на отрезке . Они принимают значения от -1 до 1. Через любую точку указанного промежутка оси ординат, равного диаметром ЕД, проводится прямая, перпендикулярная оси ординат. Таким способом получается точка с рассматриваемой ординатой.

Из свойства вытекает следующее: функция y= sin x имеет область значений (-1; 1). Утверждение записывается так: E (sin x)=(-1; 1). Максимальное значение функции равняется единице. Подобное возможно, если соответствующей точкой ЕД является точка А. Минимальное число y равно -1 в случае, когда точкой ЕД является В (х=пи/2 +2пиk, где k принадлежит области Z.

Нечётность и постоянство

Функция считается нечётной, если sin (-x)=- sin x. Её график симметричен по отношению к началу координат. Сам синус является периодической величиной, у которой наименьший положительный период. Через отрезок 2пи вид кривой повторяется. Это свойство учитывается при построении графика.

Предварительно чертится кривая на любом отрезке соответствующей длины. При переносе линии влево и вправо соблюдается шаг в kT=2 πk, где k — любая натуральная цифра. Для вычисления точек пересечения линии с осями координат используется равенство х=0. Если значение подставить в функцию, получится следующее: y=sin 0=0. В таком случае график проходит через начало координат.

Так как y равен нулю, поэтому можно рассчитать х, воспользовавшись формулой y= sin x. Координата подходящей точки ЕД равняется нулю. Такое явление будет наблюдаться только в случае, если на ЕД будут выбраны точки D либо C, при x=πk, k принадлежит Z.

Функция имеет положительное значение в первой и во второй четвертях. На этих промежутках sin x больше нуля, а любое значение х находится в пределах 0-π. При решении задач учитывается период при всех x, принадлежащих отрезку (2πk; π+2πk), где k принадлежит Z. Функция считается отрицательной в третьем и четвёртом квадрате. При этом sin меньше нуля, а иск находится в пределах (пи+2пиk; 2пи+2пиk), k принадлежит области Z.

Больше и меньше

С учётом периодичности y с периодом T=2π исследуется функция на возрастание и убывание на любом отрезке длиной в 2пи. Если T= (-π/2;3π/2), а х принадлежит данному промежутку, тогда при увеличении аргумента изменится в большую сторону и ордината. Следовательно, на указанном отрезке синусоида возрастает.

Если учитывать её периодичность, можно прийти к выводу, что она возрастает на каждом интервале (-π/2+2πk; π/2+2πk), k принадлежит Z. Если х находится на отрезке (-π/2;3π/2), тогда при увеличении аргумента ордината ЕД уменьшается, а функция убывает. С учётом периодичности синусоиды можно сделать вывод, что она бывает на каждом отрезке (π/2+2πk;3π/2+2πk), k находится в области Z.

Основываясь на проведённом исследовании, строится график y=sin x. С учётом периодичности 2π предварительно строится график на любом отрезке соответствующей длины. Чтобы точно построить точки, рекомендуется придерживаться значения синуса (ордината ЕД). На основе нечётности проводится кривая, симметричная началу координат. При этом необходимо придерживаться интервала (-π;0). Так как линия строится на отрезке длиной 2π, поэтому учитывается периодичность величины.

Вид графика повторяется на каждом отрезке с аналогичной длиной. Таким способом получается синусоида. Рассматриваемая тригонометрическая функция получила широкое применение в технике, физике и математике. Большинство процессов, включая колебания струн, напряжения в цепи, описываются с помощью функции, задаваемой формулой y= A sin (wx + f). Подобные явления считаются гармоническими колебаниями.

Кривая получается из синусоиды за счёт разных колебаний и путём параллельного переноса вдоль оси Ох. Чаще изменения результата связаны с функцией времени t. В таком случае используется формула y= A sin (wx + f), где через А обозначается амплитуда колебания, через w — частота, f — начальная фаза, 2пи/f — период колебания.

Источник

График гиперболы

Опять же вспоминаем тривиальную «школьную» гиперболу .

Выполним чертеж:
Основные свойства функции :

Область определения: .

Область значений: .

Запись  обозначает: «любое действительное число, исключая ноль»

В точке  функция терпит бесконечный разрыв. Или с помощью односторонних пределов: , . Немного поговорим об односторонних пределах. Запись  обозначает, что мы бесконечно близко приближаемся по оси  к нулю слева. Как при этом ведёт себя график? Он уходит вниз на минус бесконечность, бесконечно близко приближаясь к оси . Именно этот факт и записывается пределом . Аналогично, запись  обозначает, что мы бесконечно близко приближаемся по оси  к нулю справа.  При этом ветвь гиперболы уходит вверх на плюс бесконечность, бесконечно близко приближаясь к оси . Или коротко: .

Такая прямая (к которой бесконечно близко приближается график какой-либо функции) называется асимптотой.

В данном случае ось  является вертикальной асимптотой для графика гиперболы при .

Будет ГРУБОЙ ошибкой, если при оформлении чертежа по небрежности допустить пересечение графика с асимптотой.

Также односторонние пределы ,  говорят нам о том, что гипербола не ограничена сверху и не ограничена снизу.

Исследуем функцию на бесконечности: , то есть, если мы начнем уходить  по оси  влево (или вправо) на бесконечность, то  «игреки» стройным  шагом будут бесконечно близко приближаться к нулю, и, соответственно, ветви гиперболы бесконечно близко приближаться к оси .

Таким образом, ось  является горизонтальной асимптотой для графика функции, если «икс» стремится к плюс или минус бесконечности.

Функция  является нечётной, а, значит, гипербола симметрична относительно начала координат. Данный факт очевиден из чертежа, кроме того, легко проверяется аналитически: .

График функции вида  () представляет собой две ветви гиперболы.

Если , то гипербола расположена в первой и третьей координатных четвертях (см. рисунок выше).

Если , то гипербола расположена во второй и четвертой координатных четвертях.

Указанную закономерность места жительства гиперболы нетрудно проанализировать с точки зрения геометрических преобразований графиков.

Пример 3

Построить правую ветвь гиперболы

Используем поточечный метод построения, при этом, значения  выгодно подбирать так, чтобы делилось нацело:

Выполним чертеж:

Не составит труда построить и левую ветвь гиперболы, здесь как раз поможет нечетность функции. Грубо говоря, в таблице поточечного построения мысленно добавляем к каждому числу минус, ставим соответствующие точки и прочерчиваем вторую ветвь.

Детальную геометрическую информацию о рассмотренной линии можно найти в статье Гипербола и парабола.