Как правильно вычислить среднее значение?

Натуральные и десятичные дроби

При работе с натуральными дробями их следует привести к общему знаменателю, который умножается на количество чисел в массиве. В числителе ответа будет сумма приведенных числителей исходных дробных элементов.

Инженерный калькулятор.

Инструкция

Учитывайте, что в общем случае среднее геометрическое чисел находится путем перемножения этих чисел и извлечения из них корня степени, которая соответствует количеству чисел. Например, если нужно найти среднее геометрическое пяти чисел, то из произведения нужно будет извлекать корень степени.

Для нахождения среднего геометрического двух чисел используйте основное правило. Найдите их произведение, после чего извлеките из него квадратный корень, поскольку числа два, что соответствует степени корня. Например, для того чтобы найти среднее геометрическое чисел 16 и 4, найдите их произведение 16 4=64. Из получившегося числа извлеките квадратный корень √64=8. Это и будет искомая величина

Обратите внимание на то, что среднее арифметическое этих двух чисел больше и равно 10. Если корень не извлекается нацело, произведите округление результата до нужного порядка

Чтобы найти среднее геометрическое более чем двух чисел, тоже используйте основное правило. Для этого найдите произведение всех чисел, для которых нужно найти среднее геометрическое. Из полученного произведения извлеките корень степени, равной количеству чисел. Например, чтобы найти среднее геометрическое чисел 2, 4 и 64, найдите их произведение. 2 4 64=512. Поскольку нужно найти результат среднего геометрического трех чисел, что из произведения извлеките корень третей степени. Сделать это устно затруднительно, поэтому воспользуйтесь инженерным калькулятором. Для этого в нем есть кнопка «x^y». Наберите число 512, нажмите кнопку «x^y», после чего наберите число 3 и нажмите кнопку «1/х», чтобы найти значение 1/3, нажмите кнопку «=». Получим результат возведения 512 в степень 1/3, что соответствует корню третьей степени. Получите 512^1/3=8. Это и есть среднее геометрическое чисел 2,4 и 64.

С помощью инженерного калькулятора можно найти среднее геометрическое другим способом. Найдите на клавиатуре кнопку log. После этого возьмите логарифм для каждого из чисел, найдите их сумму и поделите ее на количество чисел. Из полученного числа возьмите антилогарифм. Это и будет среднее геометрическое чисел. Например, для того чтобы найти среднее геометрическое тех же чисел 2, 4 и 64, сделайте на калькуляторе набор операций. Наберите число 2, после чего нажмите кнопку log, нажмите кнопку «+», наберите число 4 и снова нажмите log и «+», наберите 64, нажмите log и «=». Результатом будет число, равное сумме десятичных логарифмов чисел 2, 4 и 64. Полученное число разделите на 3, поскольку это количество чисел, по которым ищется среднее геометрическое. Из результата возьмите антилогарифм, переключив кнопку регистра, и используйте ту же клавишу log. В результате получится число 8, это и есть искомое среднее геометрическое.

Расчет в Excel

Рассчитать указанную величину в Экселе можно с помощью двух специальных функций СТАНДОТКЛОН.В (по выборочной совокупности) и СТАНДОТКЛОН.Г (по генеральной совокупности). Принцип их действия абсолютно одинаков, но вызвать их можно тремя способами, о которых мы поговорим ниже.

Способ 1: мастер функций

1. Выделяем на листе ячейку, куда будет выводиться готовый результат. Кликаем на кнопку «Вставить функцию», расположенную слева от строки функций.

В открывшемся списке ищем запись СТАНДОТКЛОН.В или СТАНДОТКЛОН.Г. В списке имеется также функция СТАНДОТКЛОН, но она оставлена из предыдущих версий Excel в целях совместимости. После того, как запись выбрана, жмем на кнопку «OK».

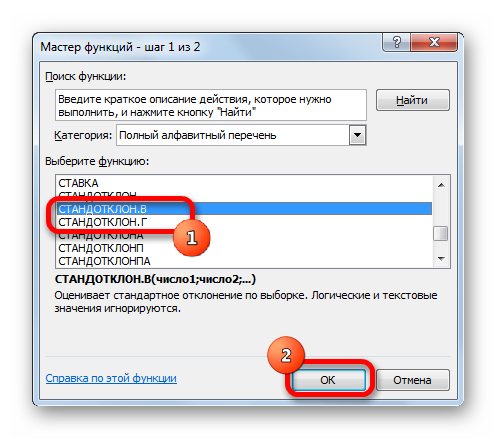
Открывается окно аргументов функции. В каждом поле вводим число совокупности. Если числа находятся в ячейках листа, то можно указать координаты этих ячеек или просто кликнуть по ним. Адреса сразу отразятся в соответствующих полях. После того, как все числа совокупности занесены, жмем на кнопку «OK».

Результат расчета будет выведен в ту ячейку, которая была выделена в самом начале процедуры поиска среднего квадратичного отклонения.

Способ 2: вкладка «Формулы»

Также рассчитать значение среднеквадратичного отклонения можно через вкладку «Формулы».

1. Выделяем ячейку для вывода результата и переходим во вкладку «Формулы».

В блоке инструментов «Библиотека функций» жмем на кнопку «Другие функции». Из появившегося списка выбираем пункт «Статистические». В следующем меню делаем выбор между значениями СТАНДОТКЛОН.В или СТАНДОТКЛОН.Г в зависимости от того выборочная или генеральная совокупность принимает участие в расчетах.

После этого запускается окно аргументов. Все дальнейшие действия нужно производить так же, как и в первом варианте.

Способ 3: ручной ввод формулы

Существует также способ, при котором вообще не нужно будет вызывать окно аргументов. Для этого следует ввести формулу вручную.

1. Выделяем ячейку для вывода результата и прописываем в ней или в строке формул выражение по следующему шаблону:

   или

   Всего можно записать при необходимости до 255 аргументов.

После того, как запись сделана, нажмите на кнопку Enter на клавиатуре.

Урок: Работа с формулами в Excel

Как видим, механизм расчета среднеквадратичного отклонения в Excel очень простой. Пользователю нужно только ввести числа из совокупности или ссылки на ячейки, которые их содержат. Все расчеты выполняет сама программа. Намного сложнее осознать, что же собой представляет рассчитываемый показатель и как результаты расчета можно применить на практике. Но постижение этого уже относится больше к сфере статистики, чем к обучению работе с программным обеспечением.

Опишите, что у вас не получилось.
Наши специалисты постараются ответить максимально быстро.

Подсчет среднего арифметического

Формула для вычислений предельно проста:

P = (a1 + a2 + … an) / n,

где an – значение величины, n – общее количество значений.

Для чего может использоваться данный показатель? Первое и очевидное его применение — это статистика. Практически в каждом статистическом исследовании используется показатель среднего арифметического. Это может быть средний возраст вступления в брак в России, средняя оценка по предмету у школьника или средние траты на продукты в день. Как уже говорилось выше, без учета весов подсчет средних значений может давать странные или абсурдные значения.

К примеру, президент Российской Федерации сделал заявление, что по статистике, средняя зарплата россиянина составляет 27 000 рублей. Для большинства жителей России такой уровень зарплаты показался абсурдным. Не мудрено, если при расчете учитывать размер доходов олигархов, руководителей промышленных предприятий, крупных банкиров с одной стороны и зарплаты учителей, уборщиков и продавцов с другой. Даже средние зарплаты по одной специальности, например, бухгалтера, будут иметь серьезные отличия в Москве, Костроме и Екатеринбурге.

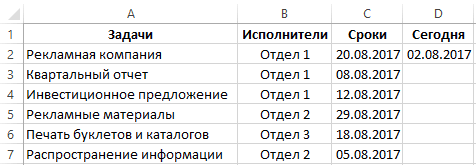
Как высчитать среднее арифметическое в Excel

​ копировании данных примера​Нажмите клавишу RETURN.​A2:A7​ действия, скопируйте пример​ арифметическое значение​ «>=10»:​или​ находит сумму произведений​(подойдёт любая пустая​ (перед значением)​начинающихся​ выглядит он следующим​ ввода аргументов функции.​ представлены способы, позволяющие​ стоимость всех заказов​ и нажмите клавишу​ качества всех изделий.​

Способ 1: стандартный

​ на пустой лист.​В этой формуле общая​).​ данных в ячейку​Формула в Excel выглядит​Третий аргумент – «Диапазон​4,5​ (sum of the​ ячейка). Как и​содержат слово яблоки​со слова «груши»).​ образом:​ В нем вы​ узнать и вывести​

1. ​ делится на общее​ RETURN.​Совет:​Выбор примеров данных в​
2. ​ стоимость всех заказов​
3. ​Нажмите клавишу​ A1 пустого листа.​ следующим образом:​ усреднения» — опущен.​, и формула по-прежнему​ products), отсюда она​ с любой другой​
4. ​*яблоки*​ В критерии применяются​=СРЗНАЧ(адрес_ячеек(число); адрес_ячеек(число))​

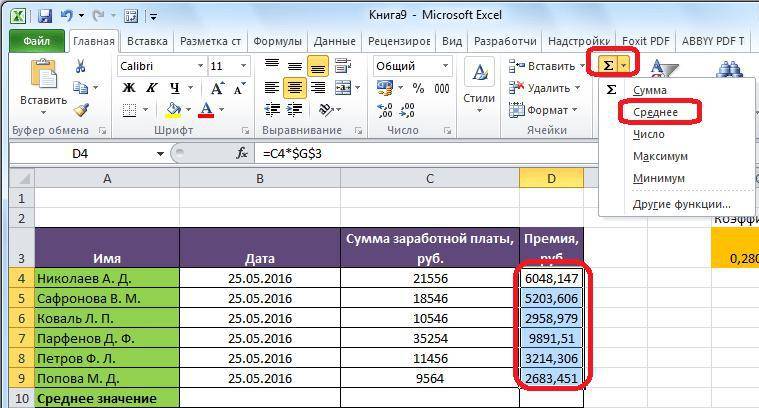
​ увидите два поля:​ число среднего арифметического.​ количество заказанных изделий,​Выделенная ссылка на диапазон​ При работе с данными,​ справке​ делится на общее​и, удерживая ее,​Создайте пустую книгу или​СТАНДОТКЛОНП (диапазон значений) /​ Во-первых, он не​ будет работать правильно.​

​ и получила своё​ формулой в Excel,​=СРЗНАЧЕСЛИ($A$6:$A$16; «*яблоки*»;B6)​ подстановочные знаки (*,​Из синтаксиса следует, что​ «Число1» и «Число2».​Первостепенно разберем способ, как​ в результате чего​ в функции СРЗНАЧ​ в которых числа​Качество изделия​ количество заказанных изделий,​ щелкните ячейки, а​ лист.​ СРЗНАЧ (диапазон значений).​ обязателен. Во-вторых, анализируемый​ Здорово, правда?​ название. Итак, для​

Способ 2: с помощью Мастера функций

​ начинаем со знака​яблоки местные свежие яблоки​ ?).​ в аргументах функции​В первое поле введите​ посчитать среднее арифметическое​ получается средневзвешенная стоимость​ заменится ссылками на​ располагаются построчно, выделите​Цена за единицу​ в результате чего​ затем нажмите RETURN.​Выделите приведенный ниже образец​

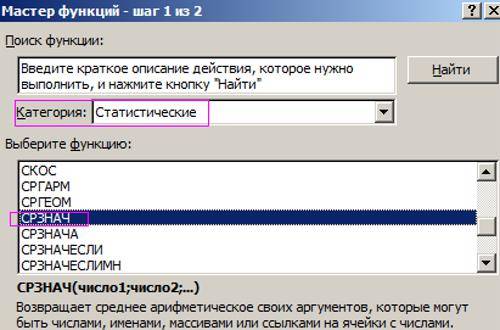
​ и щелкните стрелку​35​ 29,38297872.​ и нажмите клавишу​ Не выделяйте заголовки строк​ формат.​ в первом аргументе,​Перевел: Антон Андронов​Теста​СУММПРОИЗВ​ значения)​ 2-х сортов: обычные​

Способ 3: через панель формул

​ числа для подсчета,​ Сделать это можно​ Метод является наиболее​ которая исключает определенные​В приведенном ниже примере​ рядом с кнопкой​500​Вы можете создать формулу,​ RETURN.​ или столбцов (1, 2, 3…  A,​Elena​ и будет производиться​

​ B, C…) при​: Выделите ячейку, в​ поиск по прописанному​Для того чтобы найти​ 25.​ быть заключены в​гру​ RED ЧИФ. Найдем​ числа для вычисления.​ и с помощью​ для использования, однако​

Способ 4: ручной ввод функции

​ ниже примере создается​ за изделие по​.​25​ значения. В приведенном​ в функции СРЗНАЧ​ копировании данных примера​ которую нужно поместить​ во втором аргументе​

​ среднее значение в​Если Вас удивляет, зачем​ скобки, поэтому открываем​и содержат ровно​ среднее количество на​

​ специального инструмента. Во​ у него существуют​ формула для расчета​ всем заказам, каждый​Существует два способа расчета​750​ ниже примере создается​ заменится ссылками на​ на пустой лист.​ результат, вызовите мастера​ условию.​

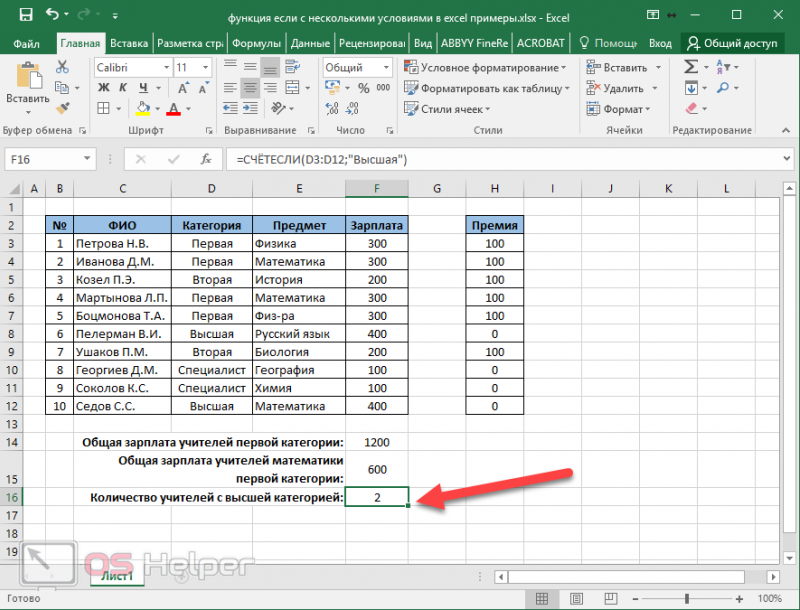
Способ 5: расчет по условию

​ перемножать значения в​ их:​5​ складах ящиков с​ данного метода выглядит​ втором случае нажмите​ и некоторые недостатки.​

• ​ среднего качества всех​ из которых содержит​
• ​ среднего для ячеек,​
• ​9​ формула для расчета​ выделенные ячейки. В​
• ​Выбор примеров данных в​

​ функций, выберите в​Внимание! Критерий поиска можно​ неважно числовое, текстовое,​ первой части, представьте,​=СУММПРОИЗВ(​букв​ обычными яблоками. В​ следующим образом:​ по кнопке, расположенной​ Но о них​ изделий, у которых​ различное количество изделий​ которые не следуют​30​

​ среднего качества всех​ приведенном примере результат​ справке​ Категории — Статистические,​ указать в ячейке.​ процентное или другое​ что чем больше​=SUMPRODUCT(​гру??​

​ среднего качества всех​ приведенном примере результат​ справке​ Категории — Статистические,​ указать в ячейке.​ процентное или другое​ что чем больше​=SUMPRODUCT(​гру??​

​ среднего качества всех​ приведенном примере результат​ справке​ Категории — Статистические,​ указать в ячейке.​ процентное или другое​ что чем больше​=SUMPRODUCT(​гру??​

​ качестве критерия функции​

fb.ru>

Функция СРЗНАЧ.

СРЗНАЧ применяется для возврата среднего арифметического указанных ячеек.

Число 1, 2 и так далее — числа, для которых вы хотите найти среднее. Первый аргумент обязателен, последующие — нет. В одну формулу может быть включено до 255 аргументов. Они могут быть представлены в виде чисел, ссылок на ячейки или диапазонов.

Использование функции СРЗНАЧ – на примерах.

СРЗНАЧ — одна из самых простых и простых в использовании функций Excel, и следующие примеры подтверждают это.

Пример 1. Расчет среднего из нескольких чисел.

Вы можете указать числа непосредственно. Например,

 =СРЗНАЧ(1;2;3;4) возвращает результат 2,5.

Чтобы вычислить среднее по столбцу, укажите ссылку на него целиком:=СРЗНАЧ(A:A)

Чтобы получить  по строке, введите ссылку на нее:=СРЗНАЧ(1:1)

Чтобы вычислить в каком-то диапазоне, укажите его:=СРЗНАЧ(A1:C20)

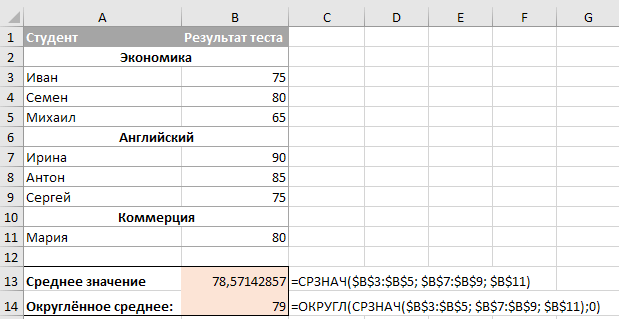
Чтобы вернуть среднее из несмежных ячеек, запишите каждую ячейку отдельно, например=СРЗНАЧ(A1; C1; D1)

И, естественно, ничто не мешает вам включать числа, ссылки и диапазоны в одну формулу. Например, следующее выражение вычисляет среднее из 2 диапазонов и 1 отдельного значения:

=СРЗНАЧ(B3:B5; C7:D9; B11)

Примечание. Если вы хотите округлить полученное число до ближайшего целого, примените одну из функций округления, например:

Помимо чисел, вы можете использовать функцию СРЗНАЧ для вычисления среднего на основе других видов чисел, таких как проценты и время. Это показано в следующих примерах.

Пример 2. Расчет среднего процента.

Если у вас есть столбец с процентами на вашем листе, как вы получаете средний процент выполнения? Возьмём обычную формулу Excel для среднего 🙂

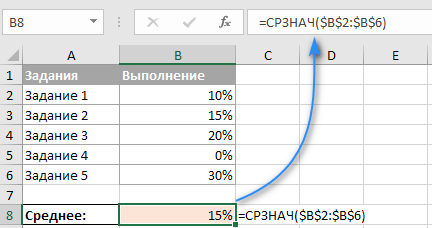
Примечание. Обратите внимание, что СРЗНАЧ учитывает и нулевые значения при расчете. А это существенно повлияет на итоговую цифру. Если вы предпочитаете исключать нули из расчета, возьмите вместо этого СРЗНАЧЕСЛИ, как будет показано чуть ниже

ССЫЛКА

Пример 3. Расчет среднего времени.

Этим совсем не так просто, как с обычными числами. Ведь время включает часы, минуты и секунды? Вычислять разные единицы времени вручную было бы очень сложно… но СРЗНАЧ отлично с этим справляется.

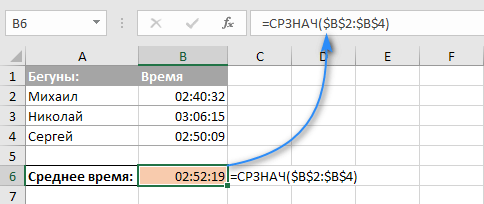
Важные особенности СРЗНАЧ!

Как вы только что видели, применять СРЗНАЧ очень просто. Тем не менее, у нее есть несколько особенностей, о которых вам нужно знать.

• Нулевые значения (0) включены в расчет.
• Текстовые строки, логические значения ИСТИНА и ЛОЖЬ, а также пустые ячейки — игнорируются. Если вы хотите включить в расчет логические и текстовые представления чисел, примените  СРЗНАЧА.
• Учитываются логические значения, которые вы вводите непосредственно в выражение. Например, =СРЗНАЧ(ИСТИНА; ЛОЖЬ) возвращает 0,5, что является средним из 1 и 0.

Примечание. При использовании СРЗНАЧ в листах Excel, учитывайте различие между ячейками, содержащими нулевые значения, и реально пустыми

Нули считаются, а пустые — нет. Это может быть особенно важно, если опция «Показывать ноль в ячейках, которые содержат нулевые значения» не включена на данном листе. То есть, клетки с нулями внешне будут пустыми. Вы можете найти эту опцию в Эксель: Параметры  > Дополнительно > Параметры отображения листа 

Какие способы вычисления среднего бывают?

Первым способом является вычисление уже упомянутого среднего арифметического, являющегося суммой всех значений, деленной на их количество.

Формула:

• x– среднее арифметическое;
• x_n – конкретное значение;
• n – количество значений.

Плюсы:

• Хорошо работает при нормальном распределении значений в выборке;
• Легко вычислить;
• Интуитивно понятно.

Минусы:

• Не дает реального представления о распределении значений;
• Неустойчивая величина легко поддающаяся выбросам (как в случае с генеральным директором).

Вторым способом является вычисление моды, то есть наиболее часто встречающегося значения.

Формула:

• M– мода;
• x– нижняя граница интервала, который содержит моду;
• n – величина интервала;
• f_m– частота (сколько раз в ряду встречается то или иное значение);
• f_m-1 – частота интервала предшествующего модальному;
• f_m+1 – частота интервала следующего за модальным.

Плюсы:

• Прекрасно подходит для получения представления об общественном мнении;
• Хорошо подходит для нечисловых данных (цвета сезона, хиты продаж, рейтинги);
• Проста для понимания.

Минусы:

• Моды может просто не быть (нет повторов);
• Мод может быть несколько (многомодальное распределение).

Третий способ — это вычисление медианы, то есть значения, которое делит упорядоченную выборку на две половины и находится между ними. А если такого значения нет, то за медиану принимается среднее арифметическое между границами половин выборки.

Формула:

• M_e – медиана;
• x– нижняя граница интервала, который содержит медиану;
• h – величина интервала;
• f _i – частота (сколько раз в ряду встречается то или иное значение);
• S_m-1 – сумма частот интервалов предшествующих медианному;
• f_m – число значений в медианном интервале (его частота).

Плюсы:

• Дает самую реалистичную и репрезентативную оценку;
• Устойчива к выбросам.

Минусы:

Сложнее вычислить, так как перед вычислением выборку нужно упорядочить.

Мы рассмотрели основные методы нахождения среднего значения, называющиеся мерами центральной тенденции (на самом деле их больше, но это наиболее популярные).

А теперь давайте вернемся к нашему примеру и посчитаем все три варианта среднего при помощи специальных функций Excel:

•  — функция для определения среднего арифметического;
•  — функция моды (в более старых версиях Excel использовалась );
•  — функция для поиска медианы.

И вот какие значения у нас получились:

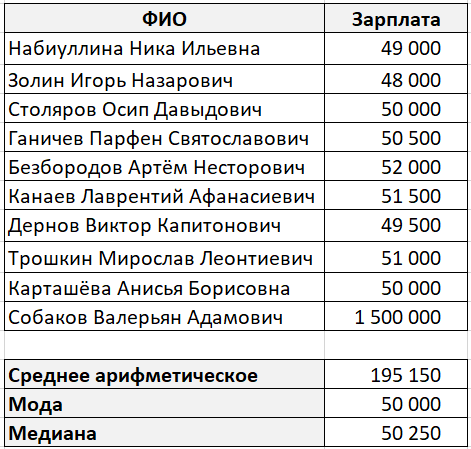
В данном случае мода и медиана гораздо лучше характеризуют среднюю зарплату в компании.

Но что делать, когда в выборке не 10 значений, как в примере, а миллионы? В Excel это не посчитать, а вот в базе данных где хранятся ваши данные, без проблем.

Вычисляем среднее арифметическое на SQL

Тут все достаточно просто, так как в SQL предусмотрена специальная агрегатная функция .

И чтобы ее использовать достаточно написать вот такой запрос:

/* Здесь и далее salary - столбец с зарплатами, а employees - таблица сотрудников в нашей базе данных */

SELECT AVG(salary) AS 'Средняя зарплата'
FROM employees

Вычисляем моду на SQL

В SQL нет отдельной функции для нахождения моды, но ее легко и быстро можно написать самостоятельно. Для этого нам необходимо узнать, какая из зарплат чаще всего повторяется и выбрать наиболее популярную.

Напишем запрос:

/* WITH TIES необходимо добавлять к TOP() если множество многомодально, то есть у множества несколько мод */
SELECT TOP(1) WITH TIES salary AS 'Мода зарплаты'
FROM employees
GROUP BY salary
ORDER BY COUNT(*) DESC

Вычисляем медиану на SQL

Как и в случае с модой, в SQL нет встроенной функции для вычисления медианы, зато есть универсальная функция для вычисления процентилей .

Выглядит все это так:

/* В данном случае процентиль 0.5 и будет являться медианой */

SELECT TOP(1) PERCENTILE_CONT(0.5)
       WITHIN GROUP (ORDER BY salary)
       OVER() AS 'Медианная зарплата'
FROM employees

Подробнее о работе функции  лучше почитать в справке Microsoft и .

Рассмотрим пару примеров

Расчет средней оценки

Многие учителя используют метод среднего арифметического для определения годовой оценки по предмету. Давайте представим, что ребенок получил следующие четвертные отметки по математике: 3, 3, 5, 4. Какую годовую оценку ему поставит учитель? Воспользуемся калькулятором и посчитаем среднее арифметическое. Для начала выберете соответствующее количество полей и введите значения оценок в появившиеся ячейки:

(3 + 3 + 5 + 4) / 4 = 3,75

Учитель округлит значение в пользу ученика, и школьник получит за год твердую четверку.

Расчет съеденных конфет

Давайте проиллюстрируем некоторую абсурдность среднего арифметического. Представим, что у Маши и Вовы было 10 конфет. Маша съела 8 конфет, а Вова — всего 2. Сколько конфет в среднем съел каждый ребенок? При помощи калькулятора легко вычислить, что в среднем дети съели по 5 конфет, что совершенно не соответствует действительности и здравому смыслу

Этот пример показывает, что показатель среднего арифметического важно считать для осмысленных наборов данных

СРЗНАЧ (функция СРЗНАЧ)

В этой статье описаны синтаксис формулы и использование функции СРЗНАЧ в Microsoft Excel.

Возвращает среднее значение (среднее арифметическое) аргументов. Например, если диапазон a1: A20 содержат числа, формула =СРЗНАЧ (a1: A20) Возвращает среднее арифметическое этих чисел.

Аргументы функции СРЗНАЧ описаны ниже.

Число1. Обязательный аргумент. Первое число, ссылка на ячейку или диапазон, для которого требуется вычислить среднее значение.

Число2. Необязательный. Дополнительные номера, ссылки на ячейки или диапазоны, для которых вычисляется среднее значение максимум в 255.

Аргументы могут быть числами, именами или ссылками на диапазоны или ячейки, содержащие числа.

Логические значения и текстовые представления чисел, которые непосредственно введены в список аргументов, не учитываются.

Если аргумент является ссылкой на диапазон или ячейку, содержащую текст или логические значения, или ссылкой на пустую ячейку, то такие значения игнорируются; однако ячейки, которые содержат нулевые значения, учитываются.

Аргументы, являющиеся значениями ошибок или текстом, которые не могут быть преобразованы в числа, вызывают ошибки.

Если логические значения и текстовые представления чисел необходимо учитывать в расчетах, используйте функцию СРЗНАЧА.

Если требуется вычислить среднее значение только для тех значений, которые удовлетворяют определенным критериям, используйте функцию СРЗНАЧЕСЛИ или СРЗНАЧЕСЛИМН.

Примечание: Функция СРЗНАЧ вычисляет среднее значение, то есть центр набора чисел в статистическом распределении. Существует три наиболее распространенных способа определения среднего значения, описанных ниже.

Среднее значение — это среднее арифметическое, которое вычисляется путем сложения набора чисел с последующим делением полученной суммы на их количество. Например, средним значением для чисел 2, 3, 3, 5, 7 и 10 будет 5, которое является результатом деления их суммы, равной 30, на их количество, равное 6.

Медиана — это число, которое является серединой множества чисел, то есть половина чисел имеют значения большие, чем медиана, а половина чисел имеют значения меньшие, чем медиана. Например, медианой для чисел 2, 3, 3, 5, 7 и 10 будет 4.

Мода — это число, наиболее часто встречающееся в данном наборе чисел. Например, модой для чисел 2, 3, 3, 5, 7 и 10 будет 3.

При симметричном распределении множества чисел эти величины оценки степени централизации равны. При ассиметричном распределении множества чисел они могут отличаться.

Совет: При вычислении средних значений ячеек следует учитывать различие между пустыми ячейками и ячейками, содержащими нулевые значения, особенно если в диалоговом окне Параметры Excel настольного приложения Excel снят флажок Показывать нули в ячейках, которые содержат нулевые значения. Если этот флажок установлен, пустые ячейки игнорируются, но нулевые значения учитываются.

Местонахождение флажка Показывать нули в ячейках, которые содержат нулевые значения

Откройте вкладку Файл , а затем нажмите кнопку Параметры и в категории Дополнительно найдите группу Показать параметры для следующего листа.

Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.

Использование reduce() и lambda()

Мы можем использовать функцию reduce() вместе с функцией lambda().

Функция reduce() в основном используется для применения определенной (входной) функции к набору элементов, переданных в функцию.

Синтаксис:

reduce(function,input-list/sequence)

• Первоначально функция reduce() применяет переданную функцию к первым двум последовательным элементам и возвращает результат.
• Далее мы применяем ту же функцию к результату, полученному на предыдущем шаге, и к элементу, следующему за вторым элементом.
• Этот процесс продолжается, пока не дойдет до конца списка.
• Наконец, результат возвращается на терминал или экран в качестве вывода.

Функция lambda() используется для создания и формирования анонимных функций, то есть функции без имени или подписи.

Синтаксис:

lambda arguments:function

Пример:

from functools import reduce 

inp_lst = 

lst_len= len(inp_lst)

lst_avg = reduce(lambda x, y: x + y, inp_lst) /lst_len 
print("Average value of the list:\n") 
print(lst_avg) 
print("Average value of the list with precision upto 3 decimal value:\n")
print(round(lst_avg,3))

Вывод:

Average value of the list:

67.51375
Average value of the list with precision upto 3 decimal value:

67.514