Python numpy guide — learn numpy arrays with examples

1.4.1.4. Basic visualization¶

Now that we have our first data arrays, we are going to visualize them.

Start by launching IPython:

$ ipython # or ipython3 depending on your install

Or the notebook:

$ jupyter notebook

Once IPython has started, enable interactive plots:

>>> %matplotlib  

Or, from the notebook, enable plots in the notebook:

>>> %matplotlib inline 

The is important for the notebook, so that plots are displayed in
the notebook and not in a new window.

Matplotlib is a 2D plotting package. We can import its functions as below:

>>> import matplotlib.pyplot as plt  # the tidy way

And then use (note that you have to use explicitly if you have not enabled interactive plots with ):

>>> plt.plot(x, y)       # line plot    
>>> plt.show()           # <-- shows the plot (not needed with interactive plots) 

Or, if you have enabled interactive plots with :

>>> plt.plot(x, y)       # line plot    

1D plotting:

>>> x = np.linspace(, 3, 20)
>>> y = np.linspace(, 9, 20)
>>> plt.plot(x, y)       # line plot    

>>> plt.plot(x, y, 'o')  # dot plot    

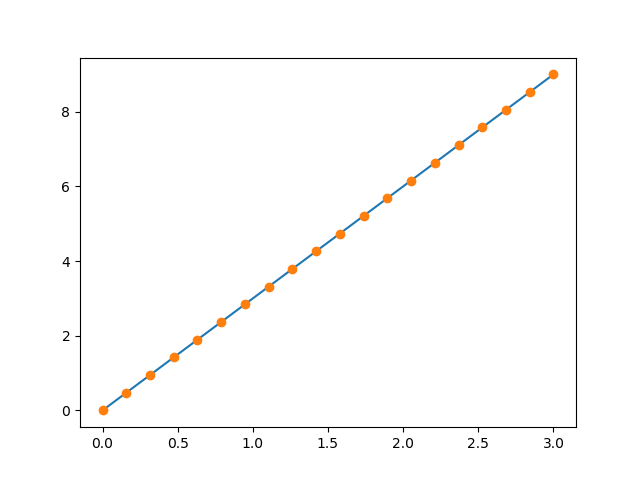
2D arrays (such as images):

>>> image = np.random.rand(30, 30)
>>> plt.imshow(image, cmap=plt.cm.hot)    
<matplotlib.image.AxesImage object at ...>
>>> plt.colorbar()    
<matplotlib.colorbar.Colorbar object at ...>

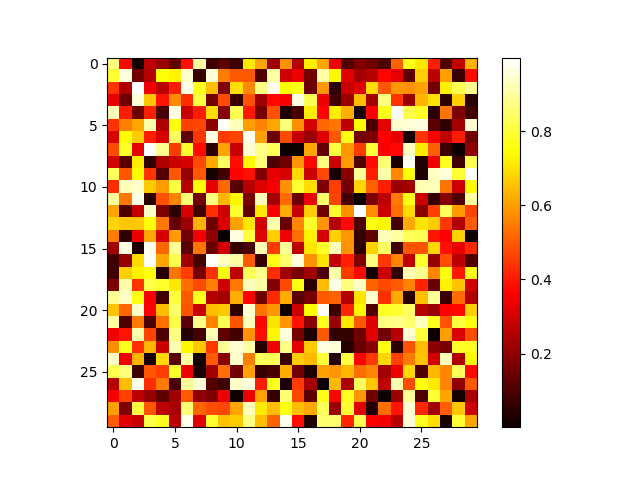
See also

More in the:

Обработка изображений в NumPy

Изображение является матрицей пикселей по размеру (высота х ширина).

Если изображение черно-белое, то есть представленное в полутонах, каждый пиксель может быть представлен как единственное число. Обычно между 0 (черный) и 255 (белый). Хотите обрезать квадрат размером пикселей в верхнем левом углу картинки? Просто попросите в NumPy .

Вот как выглядит фрагмент изображения:

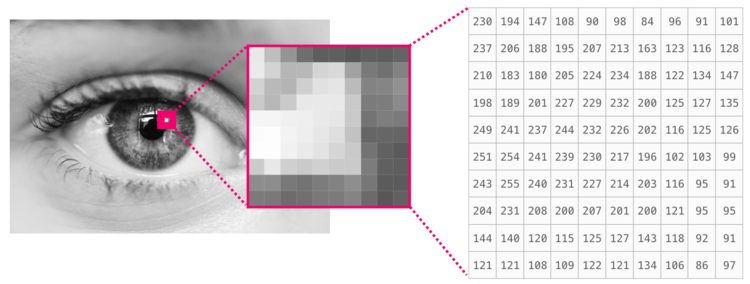
Если изображение цветное, каждый пиксель представлен тремя числами. Здесь за основу берется цветовая модель RGB — красный (R), зеленый (G) и синий (B).

В данном случае нам понадобится третья размерность, так как каждая клетка вмещает только одно число. Таким образом, цветная картинка будет представлена массивом с размерностями: (высота х ширина х 3).

Перестройка массива

После нарезки данных вам может понадобиться изменить их.

Например, некоторые библиотеки, такие как scikit-learn, могут требовать, чтобы одномерный массив выходных переменных (y) был сформирован как двумерный массив с одним столбцом и результатами для каждого столбца.

Некоторые алгоритмы, такие как рекуррентная нейронная сеть с короткой кратковременной памятью в Keras, требуют ввода данных в виде трехмерного массива, состоящего из выборок, временных шагов и функций.

Важно знать, как изменить ваши массивы NumPy, чтобы ваши данные соответствовали ожиданиям конкретных библиотек Python. Мы рассмотрим эти два примера

Форма данных

Массивы NumPy имеют атрибут shape, который возвращает кортеж длины каждого измерения массива.

Например:

При выполнении примера печатается кортеж для одного измерения.

Кортеж с двумя длинами возвращается для двумерного массива.

Выполнение примера возвращает кортеж с количеством строк и столбцов.

Вы можете использовать размер измерений вашего массива в измерении формы, например, указав параметры.

К элементам кортежа можно обращаться точно так же, как к массиву, с 0-м индексом для числа строк и 1-м индексом для количества столбцов. Например:

Запуск примера позволяет получить доступ к конкретному размеру каждого измерения.

Изменить форму 1D в 2D Array

Обычно требуется преобразовать одномерный массив в двумерный массив с одним столбцом и несколькими массивами.

NumPy предоставляет функцию reshape () для объекта массива NumPy, который можно использовать для изменения формы данных.

Функция reshape () принимает единственный аргумент, который задает новую форму массива. В случае преобразования одномерного массива в двумерный массив с одним столбцом кортеж будет иметь форму массива в качестве первого измерения (data.shape ) и 1 для второго измерения.

Собрав все это вместе, мы получим следующий проработанный пример.

При выполнении примера печатается форма одномерного массива, изменяется массив, чтобы иметь 5 строк с 1 столбцом, а затем печатается эта новая форма.

Изменить форму 2D в 3D Array

Обычно требуется преобразовать двумерные данные, где каждая строка представляет последовательность в трехмерный массив для алгоритмов, которые ожидают множество выборок за один или несколько временных шагов и одну или несколько функций.

Хорошим примером являетсямодель в библиотеке глубокого обучения Keras.

Функция изменения формы может использоваться напрямую, указывая новую размерность. Это ясно с примером, где каждая последовательность имеет несколько временных шагов с одним наблюдением (функцией) на каждый временной шаг.

Мы можем использовать размеры в атрибуте shape в массиве, чтобы указать количество выборок (строк) и столбцов (временных шагов) и зафиксировать количество объектов в 1

Собрав все это вместе, мы получим следующий проработанный пример.

При выполнении примера сначала печатается размер каждого измерения в двумерном массиве, изменяется форма массива, а затем суммируется форма нового трехмерного массива.

Тест производительности

Мы не должны чередовать векторизованную операцию numpy вместе с циклом. Это резко снижает производительность, так как код повторяется с использованием собственного.

Например, в приведенном ниже фрагменте показано, как не следует использовать numpy.

for i in np.arange(100):
    pass

Рекомендуемый способ – напрямую использовать операцию numpy.

np.arange(100)

Давайте проверим разницу в производительности с помощью модуля timeit.

import timeit
import numpy as np

# For smaller arrays
print('Array size: 1000')

# Time the average among 10000 iterations
print('range():', timeit.timeit('for i in range(1000): pass', number=10000))
print('np.arange():', timeit.timeit('np.arange(1000)', number=10000, setup='import numpy as np'))

# For large arrays
print('Array size: 1000000')

# Time the average among 10 iterations
print('range():', timeit.timeit('for i in range(1000000): pass', number=10))
print('np.arange():', timeit.timeit('np.arange(1000000)', number=10, setup='import numpy as np'))

Вывод:

Array size: 1000
range(): 0.18827421900095942
np.arange(): 0.015803234000486555
Array size: 1000000
range(): 0.22560399899884942
np.arange(): 0.011916546000065864

Как видите, numpy.arange() особенно хорошо работает для больших последовательностей. Это почти в 20 раз (!!) быстрее обычного кода Python для размера всего 1000000, который будет лучше масштабироваться только для больших массивов.

Следовательно, numpy.arange() должен быть единодушным выбором среди программистов при работе с большими массивами. Для небольших массивов, когда разница в производительности не так велика, вы можете использовать любой из двух методов.

Различные методы нормализации массива NumPy

1. Нормализация с помощью NumPy Sum

В этом методе мы используем NumPy ndarray sum для вычисления суммы каждой отдельной строки массива. После чего мы делим элементы массива if на сумму. Давайте рассмотрим это на примере.

import numpy as ppool.array(,
               )
print(a))
print(b)/b
print(c)

Выход:

Это еще один способ нормализации массива. Этот метод действительно эффективен для нормализации по строкам.

2. Нормализация с помощью sklearn

Sklearn-это модуль python, широко используемый в науке о данных и интеллектуальном анализе. Используя это href=”https://en.wikipedia.org/wiki/Method”>метод также мы можем нормализовать массив. Это следует очень простой процедуре, и давайте разберемся в ней на примере. href=”https://en.wikipedia.org/wiki/Method”>метод также мы можем нормализовать массив. Это следует очень простой процедуре, и давайте разберемся в ней на примере.

from sklearn import preprocessing
print(preprocessing.normalize(, ]))

Выход:

3. Нормализация с помощью понимания списка

Вы также можете нормализовать список в python. Понимание списка, как правило, предлагает более короткий синтаксис, который помогает в создании нового списка из существующего списка. Давайте рассмотрим это на примере.

list = ]
norm_list = [i / sum(j) for j in list for i in j]
print(norm_list)

Посмотрите, как нам удалось нормализовать наш существующий список. Здесь мы видим, что мы разделили каждый элемент в списке на сумму всех элементов. Это тоже хороший вариант для нормализации.

4. Нормализация с использованием цикла For

Мы также продвигаем процесс нормализации с помощью цикла for. Используя цикл for, мы можем вычислить сумму всех элементов. Затем разделите каждый элемент на эту сумму. Здесь я советую вам использовать массив NumPy. Продолжая деление, вы можете получить ошибку, так как “list/int” не является подходящим типом данных.

import numpy as ppool
def _sum(arr):  
      
   
      
    for i in arr: 
        + i 
          
    return(sum)  
  .array( ) (arr)  (arr)  
print (ans) /ans
print(b)

Выход:

Операции со срезами matrix в Python

Часто мы работаем не с целым массивом, а с его компонентами. Эти операции выполняются с помощью метода слайс (срез). Он пришел на замену циклу for, при котором каждый элемент подвергался перебору. Метод позволяет получать копии matrix, причём манипуляции выполняются в виде . В данном случае start — индекс элемента, с которого берётся отсчёт, stop — последний элемент, step — размер шага или число пропускаемых значений элемента при каждой итерации. Изначально start равен нулю, stop — индексу последнего элемента, step — единице. Если выполнить операции без аргументов, копирование и добавление списка произойдёт полностью.

Допустим, имеем целочисленный массив otus = . Для копирования и вывода используем otus. В итоге произойдёт вывод последовательности . Но если аргументом станет отрицательное значение, допустим, -2, произойдёт вывод уже других данных:

otus-2]; //4 

Возможны и другие операции. Например, если добавить ещё одно двоеточие, будет указан шаг копируемых элементов. Таким образом, otus позволит вывести матрицу .

Если ввести отрицательное значение, к примеру, отсчёт начнётся с конца, и в результате произойдёт вывод . Остаётся добавить, что метод среза позволяет гибко работать с матрицами и вложенными списками в Python.

Хотите узнать гораздо больше? Записывайтесь на курс «Разработчик Python»!

Установка NumPy

Я думаю, вы
прониклись уважением к этому пакету, и пришла пора прикоснуться к «святому
граалю». В начале, как всегда, его нужно установить. Сделать это чрезвычайно
просто, достаточно выполнить в терминале команду:

pip install numpy

Не удивляйтесь,
если этот пакет у вас уже установлен, так как он входит в состав многих других
библиотек. Проверить установку можно командой:

import numpy as np

Если такая
программа выполняется без ошибок, то этот «святой грааль» уже присутствует на
вашем устройстве и готов к истязаниям.

У вас здесь уже
может возникнуть вопрос: почему импорт записан в таком виде? А не просто: import
numpy? Можно и так, но тогда в программе все время придется использовать
префикс numpy. Гораздо удобнее писать две буквы «np». Поэтому
общепринятой практикой стало импортирование этого пакета именно в таком виде. Я
буду следовать сложившейся традиции и делать также.

Линейная алгебра

SciPy обладает очень быстрыми возможностями линейной алгебры, поскольку он построен с использованием библиотек ATLAS LAPACK и BLAS. Библиотеки доступны даже для использования, если вам нужна более высокая скорость, но в этом случае вам придется копнуть глубже.

Все процедуры линейной алгебры в SciPy принимают объект, который можно преобразовать в двумерный массив, и на выходе получается один и тот же тип.

Давайте посмотрим на процедуру линейной алгебры на примере. Мы попытаемся решить систему линейной алгебры, что легко сделать с помощью команды scipy linalg.solve.

Этот метод ожидает входную матрицу и вектор правой части:

# Import required modules/ libraries
import numpy as np
from scipy import linalg

# We are trying to solve a linear algebra system which can be given as:
#               1x + 2y =5
#               3x + 4y =6

# Create input array
A= np.array(,])

# Solution Array
B= np.array(,])

# Solve the linear algebra
X= linalg.solve(A,B)

# Print results
print(X)

# Checking Results
print("\n Checking results, following vector should be all zeros")
print(A.dot(X)-B)

Преобразование Fourier

Анализ Fourier помогает нам выразить функцию, как сумму периодических компонентов и восстановить сигнал из этих компонентов.

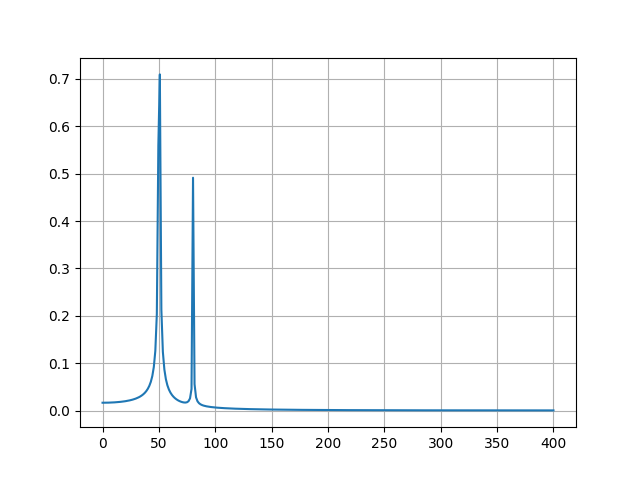
Давайте посмотрим на простой пример преобразования Fourier. Мы будем строить сумму двух синусов:

# Import Fast Fourier Transformation requirements
from scipy.fftpack import fft
import numpy as np

# Number of sample points
N = 600

# sample spacing
T = 1.0 / 800.0
x = np.linspace(0.0, N*T, N)
y = np.sin(50.0 * 2.0*np.pi*x) + 0.5*np.sin(80.0 * 2.0*np.pi*x)
yf = fft(y)
xf = np.linspace(0.0, 1.0/(2.0*T), N//2)

# matplotlib for plotting purposes
import matplotlib.pyplot as plt
plt.plot(xf, 2.0/N * np.abs(yf[0:N//2]))
plt.grid()
plt.show()

NumPy array

As discussed earlier, a Numpy array helps us in creating arrays. In this section, we will look at the syntax and different parameters associated with it. Along with that, we will also look at some examples.

Syntax of NumPy array

This is the general syntax for the function. It has several parameters associated with which we will be covering in the next section.

Parameters

1. object:array_like

This parameter represents the input array that we want as output.

2. dtype:data-type

This parameter represents the data type which the array elements will have. It is an optional parameter. By default it is not specified it will take the minimum type required to hold the elements.

3. order:

This is another optional parameter and specifies the memory layout of an array. The newly created array will be in c-order (row-major) if the object is not an array type. Also if F is specified that is (column-major) then it will take its shape.

4. ndmin:int

This optional parameter specifies the maximum number of dimension resulting array will have.

Returns

On completion of program it returns an array of specified condition.

Examples

As of now, we are done covering all the theories associated with the NumPy array. Let us now see some examples and understand how it is executed. After this, we will quickly jump to Normalize Numpy Array

import numpy as ppool
a=ppool.array(,
                ],dtype="float")
print(a)

Output:

Above we can see a simple example of NumPy array. Here we have first imported the NumPy library. After which we have used the proper syntax and also specified the dtype to be a float. In the end, our result justifies our input and hence it is verified. Similarly, you can also do it for the complex data type.

Параметр дисперсии Numpy

a = Массив, содержащий элементы, дисперсия которых должна быть вычислена

Axis = Значение по умолчанию равно none, что означает вычисление дисперсии 1D-сплющенного массива. Однако ось может быть int или кортежем ints. Если они хотят, чтобы дисперсия вычислялась вдоль какой-либо конкретной оси или осей соответственно. (Необязательно)

dtype = Тип данных, используемый при вычислении дисперсии. По умолчанию используется float64 для массивов целочисленного типа. Для массивов типов float это то же самое, что и массив

out = Альтернативный выходной массив, имеющий тот же размер, что и ожидаемый выходной массив. Но тип бросается, если это необходимо. (Необязательно)

Ddof = Относится к “Дельта-степеням свободы”: делитель, используемый при вычислении, равен N – ddof. Где N – количество элементов. ddof по умолчанию равен нулю. (Необязательно)

Keepdims = , если это значение равно True. Кроме того, уменьшенные оси возвращаются в виде массивов с размером одного измерения. С помощью этой опции результат будет правильно транслироваться по входному массиву. Для значения по умолчанию keepdims не будет передаваться в метод var() подклассов ndarray. Однако любое значение, отличное от значения по умолчанию, действительно проходит. (Необязательно)

Основы индексирования и срезы

Существует много способов выбора подмножества данных или элементов
массива. Одномерные массивы — это просто, на первый взгляд они
аналогичны спискам Python:

In : arr = np.arange(10)

In : arr
Out: array()

In : arr
Out: 5

In : arr
Out: array()

In : arr = 12

In : arr
Out: array()

Как видно, если присвоить скалярное значение срезу, как например,
, значение присваивается всем элементам среза. Первым
важным отличием от списков Python заключается в том, что срезы массива
являются представлениями исходного массива. Это означает, что данные
не копируются и любые изменения в представлении будут отражены в
исходном массиве.

Рассмотрим пример. Сначала создадим срез массива :

In : arr_slice = arr

In : arr_slice
Out: array()

Теперь, если мы изменим значения в массиве , то они
отразятся в исходном массиве :

In : arr_slice = 12345

In : arr
Out: 
array()

«Голый» срез присвоит все значения в массиве:

In : arr_slice = 64

In : arr
Out: array()

Поскольку NumPy был разработан для работы с очень большими массивами,
вы можете представить себе проблемы с производительностью и памятью,
если NumPy будет настаивать на постоянном копировании данных.

Замечание

Если вы захотите скопировать срез в массив вместо отображения, нужно
явно скопировать массив, например, .

С массивами более высокой размерности существует больше вариантов. В
двумерных массивах каждый элемент это уже не скаляр, а одномерный
массив.

In : arr2d = np.array(, , ])

In : arr2d
Out: array()

Таким образом, к отдельному элементу можно получить доступ
рекурсивно, либо передать разделенный запятыми список
индексов. Например, следующие два примера эквивалентны:

In : arr2d
Out: array()

In : arr2d[]
Out: 3

Если в многомерном массиве опустить последние индексы, то возвращаемый
объект будет массивом меньшей размерности. Например, создадим массив
размерности \( 2 \times 2 \times 3 \):

In : arr3d = np.array(, ], , ]])

In : arr3d
Out: 
array(,
        ],

       ,
        ]])

При этом — массив размерности \( 2 \times 3 \):

In : arr3d[]
Out: 
array(,
       ])

Можно присваивать как скаляр, так и массивы:

In : old_values = arr3d[].copy()

In : arr3d[] = 42

In : arr3d
Out: 
array(,
        ],

       ,
        ]])

In : arr3d[] = old_values

In : arr3d
Out: 
array(,
        ],

       ,
        ]])

Аналогично, возвращает все значения, чьи индексы
начинаются с , формируя одномерный массив:

In : arr3d
Out: array()

Это выражение такое же, как если бы мы проиндексировали в два этапа:

In : x = arr3d

In : x
Out: 
array(,
       ])

In : x[]
Out: array()

Индексирование с помощью срезов

Как одномерные объекты, такие как списки, можно получать срезы
массивов посредством знакомого синтаксиса:

In : arr
Out: array()

In : arr
Out: array()

Рассмотрим введенный выше двумерный массив . Получение срезов
этого массива немного отличается от одномерного:

In : arr2d
Out: 
array(,
       ,
       ])

In : arr2d
Out: 
array(,
       ])

Как видно, мы получили срез вдоль оси 0, первой оси. Срез, таким
образом, выбирает диапазон элементов вдоль оси. Выражение
можно прочитать как «выбираем первые две строки массива ».

Можно передавать несколько срезов:

In : arr2d
Out: 
array(,
       ])

При получении срезов мы получаем только отображения массивов того же
числа размерностей. Используя целые индексы и срезы, можно получить
срезы меньшей размерности:

In : arr2d
Out: array()

In : arr2d
Out: array()

Смотрите рис. .

Рисунок 1: Срезы двумерного массива

Синтаксис

Эта функция принимает массив типа numpy (например, массив целых и логических значений NumPy).

Он возвращает новый массив numpy после фильтрации на основе условия, который представляет собой массив логических значений, подобный numpy.

Например, условие может принимать значение массива (]), который является логическим массивом типа numpy. (По умолчанию NumPy поддерживает только числовые значения, но мы также можем преобразовать их в bool).

Например, если условием является массив (]), а наш массив – a = ndarray (]), при применении условия к массиву (a ), мы получим массив ndarray (`1 2`).

import numpy as np

a = np.arange(10)
print(a) # Will only capture elements <= 2 and ignore others

Вывод:

array()

ПРИМЕЧАНИЕ. То же условие условия также может быть представлено как <= 2. Это рекомендуемый формат для массива условий, так как записывать его как логический массив очень утомительно.

Но что, если мы хотим сохранить размерность результата и не потерять элементы из нашего исходного массива? Для этого мы можем использовать numpy.where().

numpy.where(condition )

У нас есть еще два параметра x и y. Что это? По сути, это означает, что если условие выполняется для некоторого элемента в нашем массиве, новый массив будет выбирать элементы из x.

В противном случае, если это false, будут взяты элементы из y.

При этом наш окончательный выходной массив будет массивом с элементами из x, если условие = True, и элементами из y, если условие = False.

Обратите внимание, что хотя x и y необязательны, если вы указываете x, вы также ДОЛЖНЫ указать y. Это потому, что в этом случае форма выходного массива должна быть такой же, как и входной массив

ПРИМЕЧАНИЕ. Та же логика применима как для одномерных, так и для многомерных массивов. В обоих случаях мы выполняем фильтрацию по условию. Также помните, что формы x, y и условия передаются вместе.

Теперь давайте рассмотрим несколько примеров, чтобы правильно понять эту функцию.

Агрегирование в NumPy

Дополнительным преимуществом NumPy является наличие в нем функций агрегирования:

Функциями , и дело не ограничивается.

К примеру:

• позволяет получить среднее арифметическое;
• выдает результат умножения всех элементов;
• нужно для среднеквадратического отклонения.

Это лишь небольшая часть довольно обширного списка функций агрегирования в NumPy.

Использование нескольких размерностей NumPy

Все перечисленные выше примеры касаются векторов одной размерности. Главным преимуществом NumPy является его способность использовать отмеченные операции с любым количеством размерностей.

Аудио и временные ряды в NumPy

По сути аудио файл  — это одномерный массив семплов. Каждый семпл представляет собой число, которое является крошечным фрагментов аудио сигнала. Аудио CD-качества может содержать 44 100 семплов в секунду, каждый из которых является целым числом в промежутке между -32767 и 32768. Это значит, что десятисекундный WAVE-файл CD-качества можно поместить в массив NumPy длиной в 10 * 44 100 = 441 000 семплов.

Хотите извлечь первую секунду аудио? Просто загрузите файл в массив NumPy под названием , после чего получите .

Фрагмент аудио файла выглядит следующим образом:

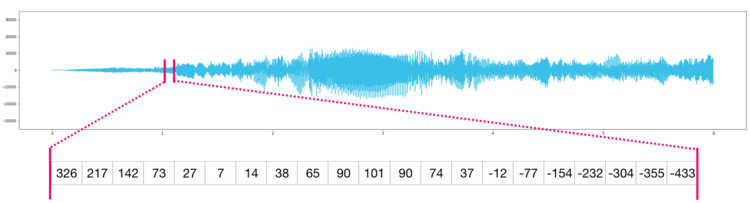
То же самое касается данных временных рядов, например, изменения стоимости акций со временем.

Вывод

В заключение можно сказать, что в этой статье мы очень подробно рассмотрели Numpy axes в python. Ось Numpy в python используется для реализации различных операций по строкам и столбцам. Такие операции, как numpy sum (), np mean() и concatenate (), достигаются путем передачи осей numpy в качестве параметров. Мы также можем перечислять данные массивов по их строкам и столбцам с помощью оси numpy. Также выделен частный случай оси для одномерных массивов. Это необходимо иметь в виду при реализации программ на python.

Однако, если у вас есть какие-либо сомнения или вопросы, дайте мне знать в разделе комментариев ниже. Я постараюсь помочь вам как можно скорее.

Счастливого Пифонирования!

Вывод

В заключение эта статья предоставляет вам всю информацию о функции Numpy variance в Python. Функция дисперсии используется для нахождения дисперсии заданного набора данных. Импорт модуля Numpy дает доступ к созданию ndarray и выполнению таких операций, как среднее стандартное отклонение. Более того, дисперсия над ним осуществляется с помощью специальных функций, встроенных в сам модуль Numpy. Вы можете обратиться к приведенным выше примерам для любых запросов, касающихся функции Numpy var() в Python.

Однако, если у вас есть какие-либо сомнения или вопросы, дайте мне знать в разделе комментариев ниже. Я постараюсь помочь вам как можно скорее.

Однако, если у вас есть какие-либо сомнения или вопросы, дайте мне знать в разделе комментариев ниже. Я постараюсь помочь вам как можно скорее.