Округление чисел

Как округлить до трех значащих цифр в Excel

В Excel все решает пользователь. Программа округлит дробные или даже целые числа в зависимости какое число значащих цифр удовлетворит потребность пользователя. Несомненно, на первый взгляд такое округление может вызывать сомнение в рациональности решения. Однако в презентациях есть место быть как точным показателям, так и относительным. И в других ситуациях это также применимо. Например, в стратегическом планировании более важные относительные показатели, так как сколько не планируй никогда не угадаешь точные результирующие числа. В тактическом планировании более важны точные значения чтобы избежать серьезных просчетов. В стратегическом планировании где показатели достигают миллионов, каждое значение ниже определенного числа значащих цифр – не существенно.

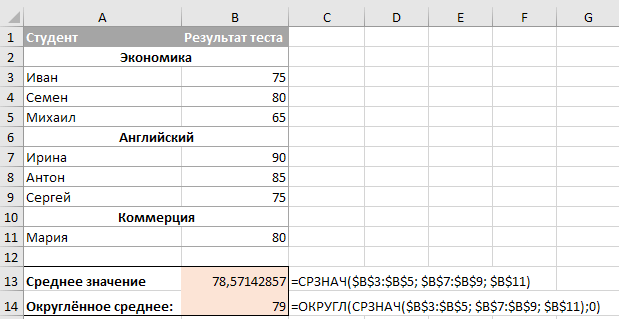
Ниже на рисунке показано, как составить формулу, которая округляет миллионные числовые значения до заданного числа значащих цифр:

Функция ОКРУГЛ используется для округления исходного числового значения до определенного количества разрядов после запятой. Функция содержит 2 аргумента:

1. Число – ссылка на исходное значение, которое необходимо округлить.
2. Число-разрядов – количество разрядов, которое необходимо оставить после округления исходного числа.

Если во втором аргументе функции ОКРУГЛ указать отрицательное число, тогда Excel округлит исходное числовое значение в соответствии цифр по левой стороне запятой. Например, следующая формула возвращает в результате вычисления число 9500:

А если указать во втором аргументе значение -3, тогда функция ОКРУГЛ возвращает результат 9000:

Такая формула прекрасно работает, но не всегда. Например, что будет если исходные числовые значения будут разных величин числовых радов? Одни будут более миллиона, другие едва превышают сотни тысяч. Если возникнет необходимость округлить все такие исходные значения до одной и той же значащей цифры используя при этом одну и туже формулу (как обычно принято в Excel). Применять для отдельных групп исходных значений функцию ОКГРУГЛ с разными значениями в аргументах – это не правильное, а точнее не наилучшее решение. Хотя теоретически все может сработать.

Для красивого решения данной задачи следует использовать постоянное неизменяемое число значащих цифр в формуле, которая вычислит соответствующие значения.

Приближенные значения

В обычной жизни мы часто встречаем два вида чисел: точные и приближенные. И если точные до сих пор были понятны, то с приближенными предстоит познакомиться в 5 классе.

У квадрата четыре стороны — число 4 невозможно оспорить, оно точное. У каждого окна есть своя ширина, и его параметры однозначно точные. А вот арбуз весит примерно 5 кг, и никакие весы не покажут абсолютно точный вес. И градусник показывает температуру с небольшой погрешностью. Поэтому вместо точных значений величин, иногда можно использовать приближенные значения.

Весы показывают, что арбуз весит 5,160 кг. Можно сказать, что арбуз весит примерно 5 кг. Это приближенное значение с недостатком.

Часы показывают время: два часа дня и пятьдесят пять минут. В разговоре про время можно сказать: «почти три» или «время около трех». Это значение времени с избытком.

Если длина платья 1м 30 см, то 1 м — это приближенное значение длины с недостатком, а 1,5 м — это приближенное значение длины с избытком.

Примерчики

Приближенное значение — число, которое получилось после округления.

Для записи результата округления используют знак «приблизительно равно» — ≈.

Округлить можно любое число — для всех чисел работают одни и те же правила.

Округлить число значит сократить его значение до сотых, десятков или тысячных, остальные значения откидываются. Это нужно в случаях, когда полная точность не нужна или невозможна.

Чтобы ребенок решал задачки на округление легко и быстро, запишите его на уроки математики в онлайн-школу Skysmart. Ученики занимаются на интерактивной платформе, задают любые неловкие вопросы и гордятся своими успехами.

Варианты округления 0,5 к ближайшему целому

Отдельного описания требуют правила округления для специального случая, когда (N+1)-й знак = 5, а последующие знаки равны нулю. Если во всех остальных случаях округление до ближайшего целого обеспечивает меньшую погрешность округления, то данный частный случай характерен тем, что для однократного округления формально безразлично, производить его «вверх» или «вниз» — в обоих случаях вносится погрешность ровно в 1/2 младшего разряда. Существуют следующие варианты правила округления до ближайшего целого для данного случая:

• Математическое округление — округление всегда в бо́льшую по модулю сторону (предыдущий разряд всегда увеличивается на единицу).
• Округление до ближайшего чётного (в английском языке известно под названием англ. banker’s rounding — «округление банкира») — округление для этого случая происходит к ближайшему чётному числу, то есть 2,5 → 2; 3,5 → 4.
• Случайное округление — округление происходит в меньшую или большую сторону в случайном порядке, но с равной вероятностью (может использоваться в статистике).
• Чередующееся округление — округление происходит в меньшую или большую сторону поочерёдно.

Во всех вариантах в случае, когда (N+1)-й знак не равен 5 или последующие знаки не равны нулю, округление происходит по обычным правилам: 2,49 → 2; 2,51 → 3.

Математическое округление просто формально соответствует общему правилу округления (см. выше). Его недостатком является то, что при округлении большого числа значений, которые далее будут обрабатываться совместно, может происходить накопление ошибки округления. Типичный пример: округление до целых рублей денежных сумм, выражаемых в рублях и копейках. В реестре из 10 000 строк (если считать копеечную часть каждой суммы случайным числом с равномерным распределением, что обычно вполне допустимо) окажется в среднем около 100 строк с суммами, содержащими в части копеек значение 50. При округлении всех таких строк по правилам математического округления «вверх» сумма «итого» по округлённому реестру окажется на 50 рублей больше точной.

Три остальных варианта как раз и придуманы для того, чтобы уменьшить общую погрешность суммы при округлении большого количества значений. Округление «до ближайшего чётного» исходит из предположения, что при большом числе округляемых значений, имеющих 0,5 в округляемом остатке, в среднем половина из них окажется слева, а половина — справа от ближайшего чётного, таким образом, ошибки округления взаимно погасятся. Строго говоря, предположение это верно лишь тогда, когда набор округляемых чисел обладает свойствами случайного ряда, что обычно верно в бухгалтерских приложениях, где речь идёт о ценах, суммах на счетах и так далее. Если же предположение будет нарушено, то и округление «до чётного» может приводить к систематическим ошибкам. Для таких случаев лучше работают два следующих метода.

Два последних варианта округления гарантируют, что примерно половина специальных значений будет округлена в одну сторону, половина — в другую. Но реализация таких методов на практике требует дополнительных усилий по организации вычислительного процесса.

• Округление в случайную сторону требует для каждой округляемой строки генерировать случайное число. При использовании псевдослучайных чисел, создаваемых линейным рекуррентным методом, для генерации каждого числа требуется операция умножения, сложения и деления по модулю, что для больших объёмов данных может существенно замедлить расчёты.
• Чередующееся округление требует хранить флаг, показывающий, в какую сторону последний раз округлялось специальное значение, и при каждой операции переключать значение этого флага.

Формула округление

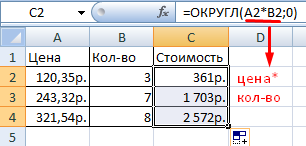
Одна из часто применяемых функций округления – ОКРУГЛ. Она работает по стандартным математическим правилам. Выбираем ячейку, щелкаем значок «Вставить функцию», категория «Математические», находим ОКРУГЛ.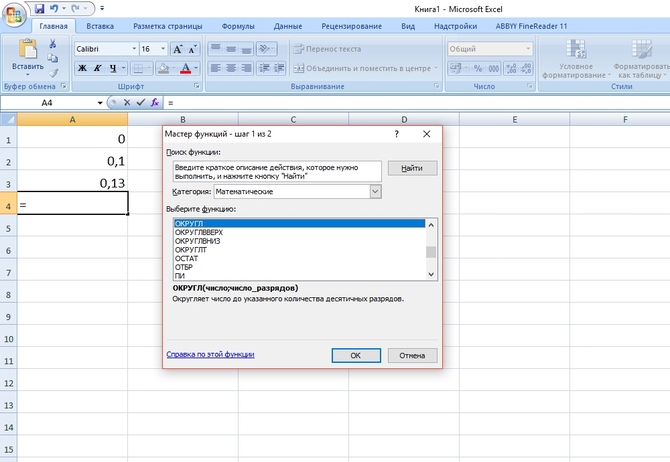

Определяем аргументы, их два – сама дробь и количество разрядов. Щелкаем «ОК» и смотрим, что получилось.

К примеру, выражение =ОКРУГЛ(0,129;1) даст результат 0,1. Нулевое количество разрядов позволяет избавляться от дробной части. Выбор отрицательного количества разрядов позволяет округлять целую часть до десятков, сотен и так далее. Например, выражение =ОКРУГЛ(5,129;-1) даст 10.

Правила округления

Коммерческое округление

В Коммерческие туры (не отрицательные числа) выглядит следующим образом :

• Если число в первом десятичном разряде равно 0, 1, 2, 3 или 4, оно округляется в меньшую сторону.
• Если число в первом десятичном разряде — 5, 6, 7, 8 или 9, то оно округляется в большую сторону.

Это правило округления описано в стандарте DIN 1333 . Округление часто уже преподается в начальной школе.

Примеры (округление до двух знаков после запятой):

• 13,3749 … € ≈ 13,37 €
• 13,3750 … € ≈ 13,38 €

Отрицательные числа в зависимости от их величины округлой формы, на 5 , чтобы сказать от нуля ( Engl : от нуля ):

• −13,3749 … € ≈ −13,37 €
• −13,3750 … € ≈ −13,38 €

В Коммерческих турах частично в правовой среде , как гражданские раунды , называемых и г. Б. в о поставщиках государственных услуг пояснил следующее:

Симметричное закругление

Коммерческое и симметричное округление отличаются друг от друга только тем, что число округляется точно посередине между двумя числами с выбранным количеством десятичных цифр.

Симметричные (или геодезическим, математический, искажаются, научный ) округление определяются следующим образом (композиция адаптирована):

1. Если число в первом десятичном разряде равно 0, 1, 2, 3 или 4, оно округляется в меньшую сторону.
2. Если число представляет собой 5 (за которыми следуют другие цифры, которые не равны нулю), 6, 7, 8 или 9 в первом десятичном разряде, оно округляется в большую сторону.
3. Если цифра в первом десятичном разряде, которую следует опустить, представляет собой только 5 (или 5, за которой следуют только нули), она округляется таким образом, чтобы последняя сохраняемая цифра была четной.

Этот тип округления используется в числовой математике , инженерии и технике. Он предусмотрен стандартом IEEE 754 для вычислений с двоичными числами с плавающей запятой в компьютерах. В англоязычной литературе это называется Round to Even или Banker’s Rounding .

Примеры (округление до одного десятичного знака):

• 2,2499 ≈ 2,2 (по правилу 1)
• 2,2501 ≈ 2,3 (по правилу 2)
• 2,2500 ≈ 2,2 (округлено до четного числа согласно правилу 3)
• 2,3500 ≈ 2,4 (округлено до четного числа согласно правилу 3)

Коммерческое округление приводит к небольшим систематическим ошибкам, так как округление на 0,5 происходит в большую сторону, а в меньшую сторону на 0,5 никогда не происходит; это может немного исказить статистику. Математическое округление всегда округляется в большую или меньшую сторону от точной середины между двумя цифрами до следующей четной цифры. В результате среднее значение округляется вверх и вниз примерно так же часто, по крайней мере, если исходные числа являются стохастическими . (Контрпример: если маленькие числа встречаются чаще, чем большие, их можно систематически округлять в меньшую сторону, чем в большую, см . Закон Бенфорда .)

Округление с сохранением суммы

В случае округления с сохранением суммы слагаемые округляются так, чтобы их сумма была равна округленной сумме слагаемых. Может потребоваться округлить некоторые слагаемые от ближайшего округленного значения до противоположного значения.

Важными приложениями являются распределение мест в пропорциональном представительстве и распределение всего НДС в счете-фактуре по его отдельным позициям.

Случай, когда все слагаемые положительные, был тщательно исследован, см. Процедуру распределения мест .

Метод Харе-Нимейера может быть обобщен для слагаемых с обоими знаками : вы округляете все числа до ближайших круглых чисел, и пока сумма слишком велика (или слишком мала), вы выбираете одно из округленных (или округленных) чисел. ) нумерует с наибольшим округление (или самое большое количество округления вниз) и изменяет его округления в направлении , противоположном. Это означает, что сумма изменений минимальна .

Допустимы ли расчеты с работниками в полных рублях?

Начислениезаработной платы округлятьнельзя:

• размер тарифной ставки (оклад) в точной сумме должен быть указан в трудовом договоре (ст. 57 ТК РФ);
• все изменения в оплате труда подписываются двусторонним письменным соглашением (ст. 72 ТК РФ).

Если округлен расчет зарплаты – значит изменен

размер тарифной ставки (оклада) без согласования сторон, а этонарушение.Выплата заработной платы

можетокругляться в большую сторону в пользу работника (Письмо Минздравсоцразвития от 07.12.2005 N 4334-17):

• округление в меньшую сторону ведет к недоплате заработной платы;
• при окончательном расчете с работником (при увольнении) следует выплатить сумму в рублях и копейках;
• порядок округления (в большую сторону) при выплате зарплаты необходимо прописать ЛНА в соответствии со ст. 8 ТК РФ.

Пособия

по нетрудоспособности и в связи с материнством, а также пособия по уходу за ребенком округлятьнельзя (Письмо ФСС от 28.01.2014 N 17-03-11/06-1026).

Округление чисел

Для нахождения приближенного значения применяется такое действие как округление чисел.

Слово «округление» говорит само за себя. Округлить число значит сделать его круглым. Круглым называется число, которое оканчивается нулём. Например, следующие числа являются круглыми:

10, 20, 30, 100, 300, 700, 1000

Любое число можно сделать круглым. Процедуру, при которой число делают круглым, называют округлением числá.

Мы уже занимались «округлением» чисел, когда делили большие числа. Напомним, что для этого мы оставляли без изменения цифру, образующую старший разряд, а остальные цифры заменяли нулями. Но это были лишь наброски, которые мы делали для облегчения деления. Своего рода лайфхак. По факту, это даже не являлось округлением чисел. Именно поэтому в начале данного абзаца мы взяли слово округление в кавычки.

На самом деле, суть округления заключается в том, чтобы найти ближайшее значение от исходного. При этом, число может быть округлено до определённого разряда — до разряда десятков, разряда сотен, разряда тысяч.

Рассмотрим простой пример на округление. Дано число 17. Требуется округлить его до разряда десятков.

Не забегая вперёд попробуем понять, что означает «округлить до разряда десятков». Когда говорят округлить число 17, то надо понимать, что от нас требуют найти ближайшее круглое число от числá 17. Причём в ходе этого поиска возможно изменения коснутся и той цифры, которая располагается в разряде десятков числá 17 (т.е цифры 1).

Предстáвим числа от 10 до 20 с помощью следующего рисунка:

На рисунке видно, что для числá 17 ближайшее круглое число это число 20. Значит ответ к задаче таким и будет: «17 приближённо равно 20″

17 ≈ 20

Мы нашли приближённое значение для 17, то есть округлили его до разряда десятков. Видно, что после округления в разряде десятков появилась новая цифра 2.

Попробуем найти приближённое число для числа 12. Для этого снова предстáвим числа от 10 до 20 с помощью рисунка:

На рисунке видно, что ближайшее круглое число для 12 это число 10. Значит ответ к задаче таким и будет: 12 приближённо равно 10

12 ≈ 10

Мы нашли приближённое значение для 12, то есть округлили его до разряда десятков. В этот раз цифра 1, которая стояла в разряде десятков в числе 12, не пострадала от округления. Почему так получилось мы расскажем позже.

Попробуем найти ближайшее число для числá 15. Снова предстáвим числа от 10 до 20 с помощью рисунка:

На рисунке видно, что число 15 одинаково удалено от круглых чисел 10 и 20. Возникает вопрос: которое из этих круглых чисел будет приближённым значением для числа 15? Для таких случаев условились принимать бóльшее число за приближённое. 20 больше чем 10, поэтому приближённое значение для 15 будет число 20

15 ≈ 20

Округлять можно и большие числа. Естественно, для них делать рисунки и изображать числа не представляется возможным. Для них существует свой способ. Например, округлим число 1456 до разряда десятков.

Итак, мы должны округлить 1456 до разряда десятков. Разряд десятков начинается на пятёрке:

Теперь о существовании первых цифр 1 и 4 временно забываем. Остается число 56

Теперь смотрим, какое круглое число находится ближе к числу 56. Очевидно, что ближайшее круглое число для 56 это число 60. Значит заменяем число 56 на число 60

Значит при округлении числа 1456 до разряда десятков полýчим 1460

1456 ≈ 1460

Видно, что после округления числа 1456 до разряда десятков, изменения коснулись и самогó разряда десятков. В новом полученном числе в разряде десятков теперь располагается цифра 6, а не 5.

Округлять числа можно не только до разряда десятков. Округлять число можно до разряда сотен, тысяч, десятков тысяч и так далее.

После того, как станóвится ясно, что округление это ни что иное как поиск ближáйшего числá, можно применять готовые правила, которые значительно облегчают округление чисел.

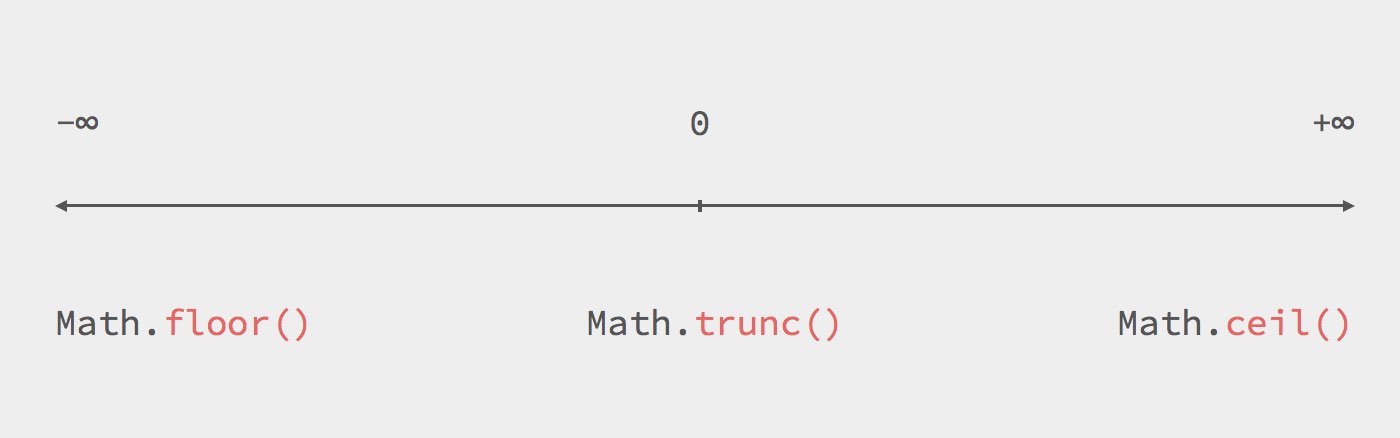
Округление в компе

Поскольку числа с плавающей запятой занимают только определенную ограниченную область памяти компьютера, точность ограничена системой. После математических операций (таких как умножение) обычно получаются числа, требующие более высокой степени точности. Чтобы по-прежнему можно было отображать результат, его необходимо каким-то образом округлить, чтобы число соответствовало предполагаемому числовому формату (например, IEEE 754 ).

Самая простая схема округления — это обрезка (англ. Truncation or chopping ): ряд определенной точки слева стоять, остальные опущены. Это округляет его до ближайшего возможного числа. Например, если вы округлите до нуля десятичных знаков, a . Этот метод очень быстрый, но он страдает относительно большой ошибкой округления (в примере это так ). Однако клиппинг — незаменимый метод цифровой обработки сигналов . Это единственный метод, который может надежно предотвратить нестабильный предельный цикл из-за ошибок округления в цифровых фильтрах .
10,112знак равно2,7510{\ displaystyle 10 {,} 11_ {2} = 2 {,} 75_ {10}}102знак равно210{\ displaystyle 10_ {2} = 2_ {10}},7510{\ displaystyle 0 {,} 75_ {10}}

Коммерческое округление также используется в качестве дополнительной схемы округления ( округление до ближайшего ). Вы добавляете число, которое нужно округлить, перед округлением, а затем отрезаете. В примере это будет означать, что он будет отрезан . Ошибка здесь только . Однако это округление искажено в лучшую сторону.
,12знак равно,510{\ displaystyle 0 {,} 1_ {2} = 0 {,} 5_ {10}}2,7510+,510знак равно3,25-е10знак равно11,012{\ displaystyle 2 {,} 75_ {10} +0 {,} 5_ {10} = 3 {,} 25_ {10} = 11 {,} 01_ {2}}112знак равно310{\ displaystyle 11_ {2} = 3_ {10}},012знак равно,25-е10{\ displaystyle 0 {,} 01_ {2} = 0 {,} 25_ {10}}

Таким образом, рассматривается математическое округление ( англ. Round-to-ближайшее четное ), которое округляет до следующего четного числа для чисел, оканчивающихся на. Эта процедура округления предусмотрена в стандарте IEEE 754. В качестве альтернативы, также округляется до ближайшего нечетного числа ( англ. Round-to-ближайшее-нечетное ).
…,…510знак равно…,…12{\ Displaystyle \ ldots {,} \ ldots 5_ {10} = \ ldots {,} \ ldots 1_ {2}}

Несмотря на то, что математическое округление хорошо работает в числовом выражении, оно по-прежнему требует полного сложения, потому что в худшем случае бит переноса проходит через все цифры числа. Поэтому он имеет относительно низкую производительность во время выполнения. Готовая таблица с округленными результатами, которую нужно только вызвать, является одним из возможных способов решения этой проблемы.

Правила округления чисел

Согласно правилу округления нужно решить, до какого числа округляется значение. После этого нужно посмотреть на цифру, которая стоит после выбранной:

• Если цифра равняется или больше 5, то значащее значение округляют с увеличением на 1.
• Если цифра меньше 5, то значение округляют без увеличения.

Рассмотрим пример округления числа после запятой. Сначала округлим до сотых число 1,235. После позиции сотых, на позиции тысячных находится число 5, значит, при округлении добавляем к сотым 1. Значит, если округлить 1,235, то получится 1,24.

Чем меньше число, до которого округляется результат, тем выше точность после округления. Можно округлять даже до десятков и сотен, однако, результаты таких округлений оставляют желать лучшего. Поэтому в большей части вычислений и округляют до сотых.

Что мы узнали?

Мы поговорили о правилах округления чисел после запятой. Узнали, как правильно округлять числа, а также рассказали, как округления влияют на точность числа. Сказали, до каких чисел округляются значения в рядовых математических вычислениях.

1. Вопрос 1 из 5

Начать тест(новая вкладка)

Округление с помощью эпсилона

Альтернативный метод JavaScript, позволяющий осуществить округление до десятых, был введен в ES6 (также известном, как JavaScript 2015). «Машинный эпсилон» обеспечивает разумный предел погрешности при сравнении двух чисел с плавающей запятой. Без округления, сравнения могут дать результаты, подобные следующим:

0.1 + 0.2 === 0.3
> false

Math.EPSILON может быть использован в функции для получения корректного сравнения:

function epsEqu(x, y) {
    return Math.abs(x - y) < Number.EPSILON * Math.max(Math.abs(x), Math.abs(y));
}

Функция принимает два аргумента: один содержит вычисления, второй ожидаемый (округленный) результат. Она возвращает сравнение этих двух параметров:

epsEqu(0.1 + 0.2, 0.3)
> true

Все современные браузеры поддерживают математические функции ES6. Но если необходимо обеспечить поддержку в старых браузерах, то нужно использовать полифиллы.

Округление в большую сторону до ближайшего целого числа

Если вы хотите округлить десятичные числа вверх, используйте Math.ceil. Действие этого метода также можно представить, как бесконечный лифт: Math.ceil всегда везет вас «вверх«, независимо от того, является ли число отрицательным или положительным:

Math.ceil(42.23);
> 43
Math.ceil(36.93);
> 37 
Math.ceil(-36.93); -36

Округление до ближайшего кратного числа

Если нужно округлить значение до ближайшего числа, кратного 5, создайте функцию, которая делит число на 5, округляет его, а затем умножает результат на то же значение:

function roundTo5(num) {
    return Math.round(num/5)*5;
}

Использование:

roundTo5(11);
> 10

Если нужно выполнить JavaScript округление до двух знаков, можно передавать функции, как начальное число, так и кратность:

function roundToMultiple(num, multiple) {
    return Math.round(num/multiple)*multiple;
}

Чтобы использовать функцию, включите в ее вызов округляемое число и кратность:

var initialNumber = 11;
var multiple = 10;
roundToMultiple(initialNumber, multiple);
> 10;

Чтобы округлять значения только в большую или меньшую сторону замените в функции round на ceil или floor.

Округление в Excel в большую сторону при помощи функции ОКРУГЛВВЕРХ

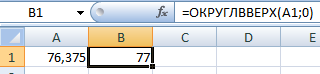
Пользователь может самостоятельно задавать направление для округления. С помощью функции ОКРУГЛВВЕРХ можно убрать лишни цифры или осуществить округление целого числа до того, которое оказывается выше.

Пример использования этой формулы можно увидеть на этом скриншоте.

6

Основное отличие этой функции от ОКРУГЛ заключается в том, что всегда функция обеспечивает округление с избытком. Если имеются какие-либо разряды числа, округление осуществляется до определенного их количества.

Синтаксис функции ОКРУГЛВВЕРХ

В состав этой функции ходит два аргумента. В целом, функция выглядит следующим образом.

=ОКРУГЛВВЕРХ(76,9;0)

А теперь давайте более подробно разберемся, какие у нее аргументы.

Аргументы функции ОКРУГЛВВЕРХ

Синтаксис у этой функции, как видим, очень простой. Аргументы следующие:1. Число. Это какое-угодно число, для которого требуется округление.

1. Число разрядов. Здесь записывается количество разрядов, которое должно остаться после того, как округление будет осуществлено.

Таким образом, по синтаксису эта формула ничем не отличается от ОКРУГЛ. От модальности числа зависит то, какие именно числа будут сокращаться. Если второй аргумент положительный, то округление оуществляется в правой части от запятой. Если же он отрицательный – то с левой.