Как нарисовать график в ворде

Элементарный график изменения

График необходим, если от человека требуется продемонстрировать, насколько определенный показатель изменился за конкретный период времени. И обычного графика для выполнения этой задачи вполне достаточно, а вот различные вычурные диаграммы на деле могут только сделать информацию менее читаемой.

Предположим, у нас есть таблица, которая предоставляет информацию о чистой прибыли компании за последние пять лет.

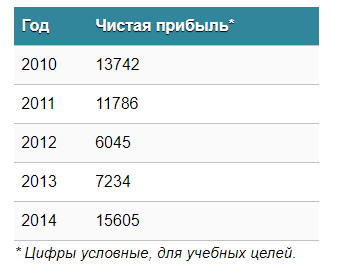
Затем отправьтесь к вкладке «Вставка», где у вас есть возможность осуществить выбор типа графика, который будет подходящим в конкретной ситуации.

2

Нас интересует тип «График». После нажатия на соответствующую кнопку, появится окошко с настройками внешнего вида будущего графика. Чтобы понять, какой вариант подходит в конкретном случае, вы можете навести указатель мыши на определенный тип, и появится соответствующее приглашение.

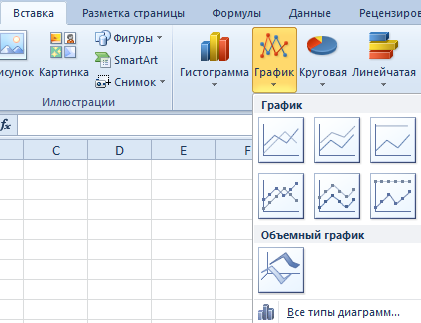
После выбора нужного вида диаграммы вам необходимо скопировать таблицу данных связать ее с графиком. Результат будет следующим.

В нашем случае на диаграмме представлено две линии. Первая имеет красный цвет. Вторая – синий. Последняя нам не нужна, поэтому мы можем удалить ее, выбрав ее и нажав кнопку «Удалить». Поскольку мы имеем лишь одну линию, легенда (блок с названиями отдельных линий графика) также может быть удалена. Но маркеры лучше назвать. Найдите панель «Работа с диаграммами» и блок «Подписи данных» на вкладке «Макет». Здесь вы должны определить положение чисел.

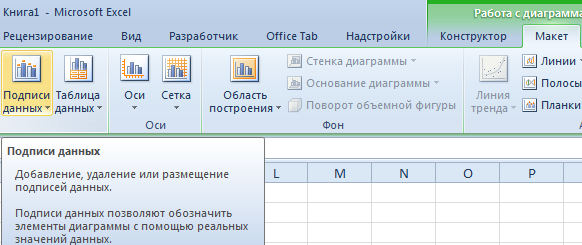
Оси рекомендуется называть, чтобы обеспечить большую удобочитаемости графика. На вкладке «Макет» найдите меню «Названия осей» и задайте имя для вертикальной или горизонтальной осей соответственно.

Но вы можете смело обходиться без заголовка. Чтобы удалить его, вам нужно переместить его в область графика, которая невидима для постороннего глаза (над ним). Если вам все еще нужно название диаграммы, вы можете получить доступ ко всем необходимым настройкам через меню «Название диаграммы» на той же вкладке. Вы также можете найти его на вкладке «Макет».

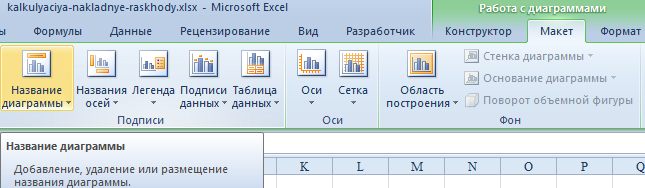
Вместо порядкового номера отчетного года достаточно оставить только сам год. Выберите требуемые значения и щелкните по ним правой кнопкой мышки. Затем кликните по пункту «Выбор данных» – «Изменить подпись горизонтальной оси». Далее вам следует задать диапазон. В случае с нами, это первая колонка таблицы, являющейся источником информации. Результат такой.

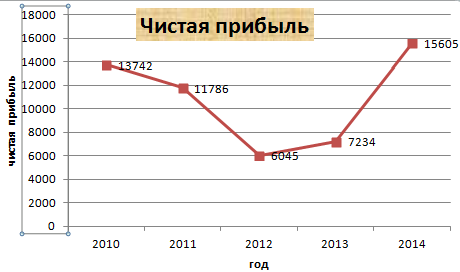
Но вообще, можно все оставить, этот график вполне рабочий. Но если есть необходимость сделать привлекательный дизайн графика, то к вашим услугам – Вкладка “Конструктор”, которая позволяет указать фоновый цвет графика, его шрифт, а также разместить его на другом листе.

Исследование функции

Важные точки графика функции y = f(x):

• стационарные и критические точки;
• точки экстремума;
• нули функции;
• точки разрыва функции.

Стационарные точки — точки, в которых производная функции f(x) равна нулю.

Критические точки — точки, в которых производная функции f(x) равна нулю либо не существует. Стационарные точки являются подмножеством множества критических точек.

Экстремум в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума.

Нули функции — это значения аргумента, при которых функция равна нулю.

Асимптота — прямая, которая обладает таким свойством, что расстояние от точки графика функции до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат. По способам их отыскания выделяют три вида асимптот: вертикальные, горизонтальные, наклонные.

Функция непрерывна в точке k, если предел функции в данной точке равен значению функции в этой точке:

Если функция f(x) не является непрерывной в точке x = a, то говорят, что f(x) имеет разрыв в этой точке.

Если нам нужно построить график незнакомой функции, когда заранее невозможно представить вид графика, полезно применять схему исследования свойств функции. Она поможет составить представление о графике и приступить к построению по точкам.

Схема построения графика функции:

1. Найти область определения функции.
2. Найти область допустимых значений функции.
3. Проверить не является ли функция четной или нечетной.
4. Проверить не является ли функция периодической.
5. Найти нули функции.
6. Найти промежутки знакопостоянства функции, то есть промежутки, на которых она строго положительна или строго отрицательна.
7. Найти асимптоты графика функции.
8. Найти производную функции.
9. Найти критические точки в промежутках возрастания и убывания функции.
10. На основании проведенного исследования построить график функции.

У нас есть отличные онлайн занятия по математике для учеников с 1 по 11 классы! Приходи на пробное занятие с нашими лучшими преподавателями!

График функции

Он представляет собой одну из ветвей параболы. Выполним чертеж:

Основные свойства функции :

Область определения: .

Область значений: .

То есть, график функции полностью находится в первой координатной четверти.

Функция  не ограничена сверху. Или с помощью предела:

При построении простейших графиков с корнями также уместен поточечный способ построения, при этом выгодно подбирать такие значения «икс», чтобы корень извлекался нацело:

На самом деле хочется разобрать еще примеры с корнями, например, , но они встречаются значительно реже. Сейчас я ориентируюсь на более распространенные случаи, и, как показывает практика, что-нибудь вроде  приходиться строить значительно чаще. Однако унывать не нужно, в других статьях я рассмотрю самые разнообразные функции и их графики, корни в том числе.

Построение графика функции f(x)

Возможно самой распространенной задачей в студенческой и инженерной практике является построение графика функции f(x). В mathcad это делается в следующем порядке. С помощью клавиатуры и панели calculator вводится функция f(x), как показано на рис. 6. Для создания функции необходимо использовать равно с двоеточием «:=» (опертор присваивания). Далее в панели Graph найдите иконку X-Y Plot, щелкните по ней и создайте заготовку для графика. В черных прямоугольниках-маркерах введите имя функции и название аргумента. После отображения кривой зайдите в свойства графика и настройте отображение вашей кривой

Рис. 6. Построение графика функции f(x)

Чтобы построить два графика и более на одном поле (в тех же осях координат) сделайте следующее: введите вторую функцию, например y(x):=…., поместите курсор мыши в маркер поля графика, где уже указана первая функция f(x) и введите запятую. Таким образом mathcad зоздаст второй маркер для ввода очередной функции. Введите вашу вторую функцию и нажмите enter. Если имя аргумента обеих функций совпадает, то вторая кривая отобразится в поле графика, в противном случае, под осью абсцисс введите через запятую имя аргумента второй функции. Образец можно посмотреть ниже на рис. 7

Рис. 7. Построение двух графиков функции

Общая схема исследования

Для чего нужно это исследование, спросите вы, если есть множество сервисов, которые построят для самых замудренных функций? Для того, чтобы узнать свойства и особенности данной функции: как ведет себя на бесконечности, насколько быстро меняет знак, как плавно или резко возрастает или убывает, куда направлены «горбы» выпуклости, где не определены значения и т.п.

А уже на основании этих «особенностей» и строится макет графика — картинка, которая на самом-то деле вторична (хотя в учебных целях важна и подтверждает правильность вашего решения).

Начнем, конечно же, с плана. Исследование функции — объемная задача (пожалуй, самая объемная из традиционного курса высшей математики, обычно от 2 до 4 страниц с учетом чертежа), поэтому, чтобы не забыть, что в каком порядке делать, следуем пунктам, описанным ниже.

Алгоритм

1. Найти область определения. Выделить особые точки (точки разрыва).
2. Проверить наличие вертикальных асимптот в точках разрыва и на границах области определения.
3. Найти точки пересечения с осями координат.
4. Установить, является ли функция чётной или нечётной.
5. Определить, является ли функция периодической или нет (только для тригонометрических функций).
6. Найти точки экстремума и интервалы монотонности.
7. Найти точки перегиба и интервалы выпуклости-вогнутости.
8. Найти наклонные асимптоты. Исследовать поведение на бесконечности.
9. Выбрать дополнительные точки и вычислить их координаты.
10. Построить график и асимптоты.

В разных источниках (учебниках, методичках, лекциях вашего преподавателя) список может иметь отличный от данного вид: некоторые пункты меняются местами, объединяются с другими, сокращаются или убираются. Учитывайте требования/предпочтения вашего учителя при оформлении решения.

Схема исследования в формате pdf: скачать.

Как построить график функции онлайн на этом сайте?

Чтобы построить график функции онлайн, нужно просто ввести свою функцию в специальное поле и кликнуть куда-нибудь вне его. После этого график введенной функции нарисуется автоматически. Допустим, вам требуется построить классический график функции «икс в квадрате». Соответственно, нужно ввести в поле «x^2».

Если вам нужно построить график нескольких функций одновременно, то нажмите на синюю кнопку «Добавить еще». После этого откроется еще одно поле, в которое надо будет вписать вторую функцию. Ее график также будет построен автоматически.

Цвет линий графика вы можете настроить с помощью нажатия на квадратик, расположенный справа от поля ввода функции. Остальные настройки находятся прямо над областью графика. С их помощью вы можете установить цвет фона, наличие и цвет сетки, наличие и цвет осей, наличие рисок, а также наличие и цвет нумерации отрезков графика. Если необходимо, вы можете масштабировать график функции с помощью колесика мыши или специальных иконок в правом нижнем углу области рисунка.

После построения графика и внесения необходимых изменений в настройки, вы можете скачать график с помощью большой зеленой кнопки «Скачать» в самом низу. Вам будет предложено сохранить график функции в виде картинки формата PNG.

Построение графика в полярных координатах в mathcad

Введите функцию, которую необходимо построить в полярных координатах. Для примера возьмем y(x):=2*sin(3*x+0.5)

Для построения графика в полярных координатах нажмите кнопку Polar Plot из панели Graph

Рис. 13. Создание загатовки для графика в полярных координатах

Вы увидете пустое поле графика. В черном маркере слева введите имя введенной функции y(x). В маркере снизу введите аргумент x и нажмите enter. Вы увидете «трилистник». Внешний вид графика можно настроить щелкнув два раза по графику левой кнопкой мыши. В появившемся окне представлен широкий набор инструментов для настройки отображения.

Сдвиг графика влево/вправо вдоль оси абсцисс

Если к АРГУМЕНТУ функции  добавляется константа, то происходит сдвиг (параллельный перенос) графика вдоль оси . Рассмотрим функцию  и положительное число :

Правила:
1) чтобы построить график функции , нужно график  сдвинуть ВДОЛЬ оси  на  единиц влево;
2) чтобы построить график функции , нужно график  сдвинуть ВДОЛЬ оси  на  единиц вправо.

Пример 6

Построить график функции

Берём параболу  и сдвигаем её вдоль оси абсцисс на 1 единицу вправо:
«Опознавательным маячком» служит значение , именно здесь находится вершина параболы .

Теперь, думаю, ни у кого не возникнет трудностей с построением графика  (демонстрационный пример начала урока) – кубическую параболу  нужно сдвинуть на 2 единицы влево.

Вот ещё один характерный случай:

Пример 7

Построить график функции

Гиперболу  (чёрный цвет) сдвинем вдоль оси  на 2 единицы влево: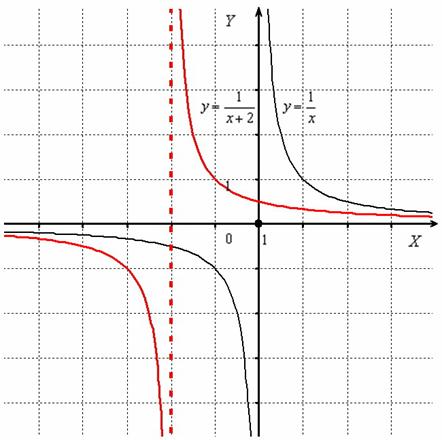
Перемещение гиперболы «выдаёт» значение, которое не входит в область определения функции. В данном примере , и уравнение прямой   задаёт вертикальную асимптоту (красный пунктир) графика функции  (красная сплошная линия). Таким образом, при параллельном переносе асимптота графика тоже сдвигается (что очевидно).

Вернёмся к тригонометрическим функциям:

Пример 8

Построить график функции  

График синуса  (чёрный цвет) сдвинем вдоль оси  на  влево: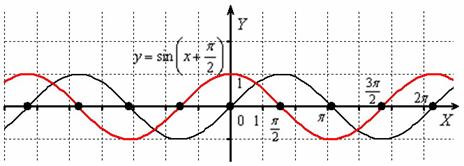
Внимательно присмотримся к полученному красному графику …. Это в точности график косинуса ! По сути, мы получили геометрическую иллюстрацию формулы приведения , и перед вами, пожалуй, самая «знаменитая» формула, связывающая данные тригонометрические функции.  График  функции  получается путём сдвига синусоиды  вдоль оси  на  единиц влево (о чём уже говорилось на уроке Графики и свойства элементарных функций). Аналогично можно убедиться в справедливости любой другой формулы приведения.

Рассмотрим композиционное правило, когда аргумент представляет собой линейную функцию: , при этом параметр «ка» не равен нулю или единице, параметр «бэ» – не равен нулю. Как построить график такой функции? Из школьного курса мы знаем, что умножение имеет приоритет перед сложением, поэтому, казалось бы, сначала график сжимаем/растягиваем/отображаем в зависимости от значения , а потом сдвигаем на  единиц. Но здесь есть подводный камень, и корректный алгоритм таков:

Аргумент функции необходимо представить в виде  и последовательно выполнить следующие преобразования:

1) График функции  сжимаем (или растягиваем) к оси (от оси) ординат: (если , то график дополнительно следует отобразить симметрично относительно оси ).

2) График полученной функции  сдвигаем влево (или вправо) вдоль оси  абсцисс на  (!!!) единиц, в результате чего будет построен искомый график .

Пример 9

Построить график функции  

Представим функцию в виде  и выполним следующие преобразования: синусоиду  (чёрный цвет):

1) сожмём к оси  в два раза: (синий цвет);
2) сдвинем вдоль оси  на  (!!!) влево:  (красный цвет):
Пример вроде бы несложный, а пролететь с параллельным переносом легче лёгкого. График сдвигается на , а вовсе не на .

Продолжаем расправляться с функциями начала урока:

Пример 10

Построить график функции  

Представим функцию в виде . В данном случае:  Построение проведём в три шага. График натурального логарифма :

1) сожмём к оси  в 2 раза: ;
2) отобразим симметрично относительно оси : ;
3) сдвинем вдоль оси  на  (!!!) вправо: :
Для самоконтроля в итоговую функцию  можно подставить пару значений «икс», например,  и свериться с полученным графиком.

В рассмотренных параграфах события происходили «горизонтально» – гармонь играет, ноги пляшут влево/вправо. Но похожие преобразования происходят и в «вертикальном» направлении – вдоль оси . Принципиальное отличие состоит в том, что связаны они не с АРГУМЕНТОМ, а с САМОЙ ФУНКЦИЕЙ.

Как построить график онлайн?

Даже если преподаватель требует вас сдавать задание, написанное от руки, с чертежом на листке в клеточку, вам будет крайне полезно во время решения построить график в специальной программе (или сервисе), чтобы проверить ход решения, сравнить его вид с тем, что получается вручную, возможно, найти ошибки в своих расчетах (когда графики явно ведут себя непохоже).

Ниже вы найдете несколько ссылок на сайты, которые позволяют построить удобно, быстро, красиво и, конечно, бесплатно графики практически любых функций. На самом деле таких сервисов гораздо больше, но стоит ли искать, если выбраны лучшие?

Графический калькулятор Desmos

Desmos.com
Невероятно гибкий и функциональный графический калькулятор. Интутивно понятно вводятся формулы (прямо на ходу преобразуются), автоматически подбираются масштаб и цвета графика для максимальной наглядности. Например, для функции $y(x)=\frac{x^3}{4(x-2)^2}$ буквально за минуту построены основной график и асимптоты, вот что получилось:

При этом сайт сам пометил важные точки на графике (см. серым): локальный экстремум, пересечение с осями.

Вы можете менять масштаб, цвета, вид линий; добавлять на график точки, линии, кривые, табличные данные и даже анимацию!

Посмотрите, какую красоту Desmos умеет рисовать (точнее, его пользователи):

Сайт для построения графиков y(x).ru

y(x).ru
Это уже наш продукт, возможно, не такой красивый и интерактивный, но вполне подходящий для учебных целей. Можно строить онлайн несколько графиков одновременно, при этом выбирать и обычный, и параметрический вид, и даже задание в полярных координатах. Цвет и масштаб можно менять вручную. Вот так вводятся графики:

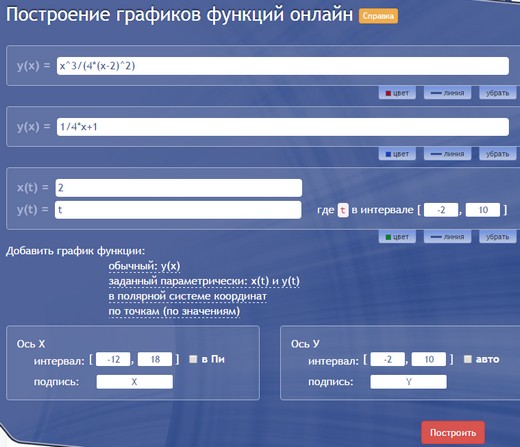
И такой график получается в итоге:

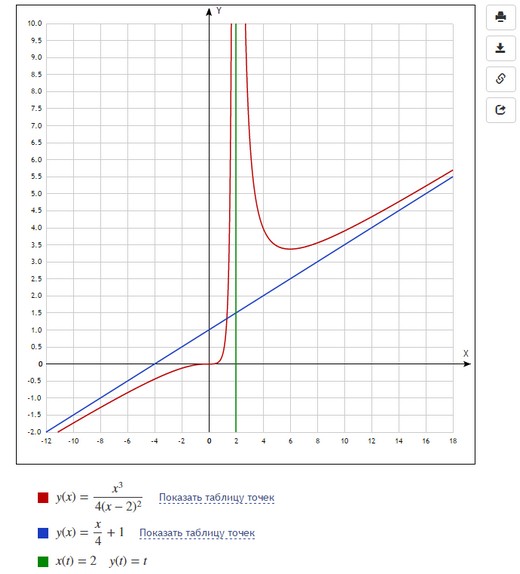
Из минусов можно заметить, что вводить, например, горизонтальные асимптоты не так просто: если в Desmos мы просто написали $x=2$, то здесь пришлось вводить параметрическую функцию $x(t)=2, y(t)=t$. Цвета и масштаб тоже пришлось подбирать вручную (иначе все графики оказались бы красными и мелкими).

Другие сайты

Еще несколько сервисов, которые обладают меньшим удобством/функциональностью, но тоже достойны внимания:

• ru.numberempire.com Можно построить сразу несколько функций, цвета подбираются автоматически, график интерактивный (положение и масштаб меняются мышкой).
• mathsolution.ru Можно строить несколько графиков, выбирая толщину линий и цвет, скрывать/отображать сетку, менять масштаб, сохранять картинки в файл.
• easyto.me При построении нескольких графиков на одном поле предыдущие не редактируются. В остальном функции как у прежних: выбор цвета, толщины линии, масштаба чертежа.
• grafikus.ru Кроме обычных графиков можно также строить трехмерные (3d). Можно построить несколько графиков разного типа (обычный,параметрический, в полярных координатах). Цвет и толщину линии выбрать нельзя. Интерактивности нет

OnlineCharts.ru

Еще одно отличное приложение для эффектного представления информации вы можете найти на сайте OnlineCharts.ru, где можно построить график функции онлайн бесплатно.

Сервис способен работать с множеством видов диаграмм, включая линейные, пузырьковые, круговые, столбчатые и радиальные.

Система обладает очень простым и наглядным интерфейсом. Все доступные функции разделены вкладками в виде горизонтального меню.

Чтобы начать работу необходимо выбрать тип диаграммы, которую вы хотите построить.

После этого можно настроить некоторые дополнительные параметры внешнего вида, в зависимости от выбранного типа графика.

Во вкладке «Добавить данные» пользователю предлагается задать количество строк и если необходимо количество групп.

Также можно определить цвет.

Обратите внимание! Вкладка «Подписи и шрифты» предлагает задать свойства подписей (нужно ли их выводить вообще, если да, то каким цветом и размером шрифта). Также предоставляется возможность выбора типа шрифта и его размера для основного текста диаграммы

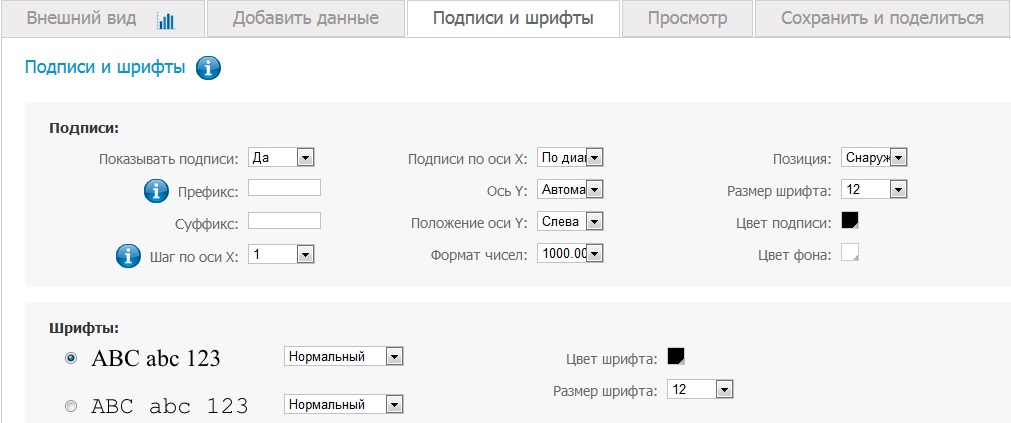
Нажимаем далее и попадаем во вкладку «Просмотр», где получаем возможность созерцать плоды своего труда.

На вкладке «Сохранить и поделиться диаграммой» есть возможность отправить ссылку на созданный график друзьям или поделиться своей работой через социальные сети.

Все предельно просто.

Полный пример решения онлайн

Спасибо за ваши закладки и рекомендации

Провести полное исследование и построить график функции
$$
y(x)=\frac{x^2+8}{1-x}.
$$

1) Область определения функции. Так как функция представляет собой дробь, нужно найти нули знаменателя.
$$1-x=0, \quad \Rightarrow \quad x=1.$$
Исключаем единственную точку $x=1$ из области определения функции и получаем:
$$
D(y)=(-\infty; 1) \cup (1;+\infty).
$$

2) Исследуем поведение функции в окрестности точки разрыва. Найдем односторонние пределы:

Так как пределы равны бесконечности, точка $x=1$ является разрывом второго рода, прямая $x=1$ — вертикальная асимптота.

3) Определим точки пересечения графика функции с осями координат.

Найдем точки пересечения с осью ординат $Oy$, для чего приравниваем $x=0$:

Таким образом, точка пересечения с осью $Oy$ имеет координаты $(0;8)$.

Найдем точки пересечения с осью абсцисс $Ox$, для чего положим $y=0$:

Уравнение не имеет корней, поэтому точек пересечения с осью $Ox$ нет.

Заметим, что $x^2+8>0$ для любых $x$. Поэтому при $x \in (-\infty; 1)$ функция $y>0$ (принимает положительные значения, график находится выше оси абсцисс), при $x \in (1; +\infty)$ функция $y\lt 0$ (принимает отрицательные значения, график находится ниже оси абсцисс).

4) Функция не является ни четной, ни нечетной, так как:

5) Исследуем функцию на периодичность. Функция не
является периодической, так как представляет собой дробно-рациональную функцию.

6) Исследуем функцию на экстремумы и монотонность. Для этого найдем первую производную функции:

Приравняем первую производную к нулю и найдем стационарные точки (в которых $y’=0$):

Получили три критические точки: $x=-2, x=1, x=4$. Разобьем всю область определения функции на интервалы данными точками и определим знаки производной в каждом промежутке:

При $x \in (-\infty; -2), (4;+\infty)$ производная $y’ \lt 0$, поэтому функция убывает на данных промежутках.

При $x \in (-2; 1), (1;4)$ производная $y’ >0$, функция возрастает на данных промежутках.

При этом $x=-2$ — точка локального минимума (функция убывает, а потом возрастает), $x=4$ — точка локального максимума (функция возрастает, а потом убывает).

Найдем значения функции в этих точках:

Таким образом, точка минимума $(-2;4)$, точка максимума $(4;-8)$.

7) Исследуем функцию на перегибы и выпуклость. Найдем вторую производную функции:

Приравняем вторую производную к нулю:

Полученное уравнение не имеет корней, поэтому точек перегиба нет. При этом, когда $x \in (-\infty; 1)$ выполняется $y» \gt 0$, то есть функция вогнутая, когда $x \in (1;+\infty)$ выполняется $y» \lt 0$, то есть функция выпуклая.

8) Исследуем поведение функции на бесконечности, то есть при .

Так как пределы бесконечны, горизонтальных асимптот нет.

Попробуем определить наклонные асимптоты вида $y=kx+b$. Вычисляем значения $k, b$ по известным формулам:

Получили, у что функции есть одна наклонная асимптота $y=-x-1$.

9) Дополнительные точки. Вычислим значение функции в некоторых других точках, чтобы точнее построить график.

10) По полученным данным построим график, дополним его асимптотами $x=1$ (синий), $y=-x-1$ (зеленый) и отметим характерные точки (фиолетовым пересечение с осью ординат, оранжевым экстремумы, черным дополнительные точки):

Зачем нужно строить график функции?

На этой странице вы можете построить интерактивный график функции онлайн. Построение графика функции позволяет увидеть геометрический образ той или иной математической функции. Для того чтобы вам было удобнее строить такой график, мы создали специальное онлайн приложение. Оно абсолютно бесплатно, не требует регистрации и доступно для использования прямо в браузере без каких-либо дополнительных настроек и манипуляций. Строить графики для разнообразных функций чаще всего требуется школьникам средних и старших классов, изучающим алгебру и геометрию, а также студентам первых и вторых курсов в рамках прохождения курсов высшей математики. Как правило, данный процесс занимает много времени и требует кучу канцелярских принадлежностей, чтобы начертить оси графика на бумаге, проставить точки координат, объединить их ровной линией и т.д. С помощью данного онлайн сервиса вы сможете рассчитать и создать графическое изображение функции моментально.

Работа с диаграммами в Экселе

Теперь, когда круговая диаграмма, гистограмма или график готовы, нужно придать им более привлекательный вид, обеспечивающий зрителю наилучшее понимание. К главным параметрам рисунка относятся наименование, легенда и подписи данных; о настройке этих элементов в Экселе будет подробнее рассказано далее.

Выбор названия диаграммы

Задать наименование диаграммы в Excel можно, следуя простому алгоритму:

Выделить щелчком левой клавиши мыши блок с названием.

Ещё раз щёлкнуть, не перемещая указателя, и ввести в текстовом поле новое наименование, более подходящее к случаю.

Другой вариант — щёлкнуть правой клавишей мыши по блоку с наименованием, выбрать в контекстном меню пункт «Изменить текст» и ввести требуемый.

Здесь же, в разделе «Шрифт», юзер может выбрать начертание, кегль и другие параметры текста, подтвердив изменения нажатием на кнопку «ОК».

Чтобы вернуть всё «как было», нужно вновь вызвать контекстное меню и щёлкнуть по строчке «Восстановить стиль».

Настроить название можно, кликнув по полю диаграммы и нажав на «плюсик» в правом верхнем его углу.

В выплывающем меню пользователю нужно выбрать, следует ли размещать название (для отмены достаточно снять галочку в чекбоксе), а также где именно оно должно находиться.

Пункт «Дополнительные параметры» открывает доступ к тонким настройкам названия изображения.

Если название диаграммы было изменено вручную, а теперь требуется вернуть автоматическое наименование (по заголовку соответствующего столбца), следует убрать галочку в чекбоксе или воспользоваться клавишей Delete — рисунок останется без текстового блока.

И снова, нажав на «плюсик», вернуть галочку на место.

Манипуляции с легендой

Ещё большей ясности создатель диаграммы в Экселе может добиться, добавив на рисунок легенду — специальное поле с описанием представленных данных. Сделать это можно следующим образом:

Перейти на вкладку «Конструктор», щёлкнуть по кнопке «Добавить элемент диаграммы» и во вложенном списке «Легенда» выбрать место размещения блока данных: снизу, сверху, справа или слева.

То же самое можно сделать, щёлкнув по полю диаграммы, затем по «плюсику» возле него, установив галочку в чекбоксе с тем же названием и указав в выпадающем меню, где именно будет находиться легенда.

Зайдя в подраздел «Дополнительные параметры», юзер сможет точнее настроить размещение блока, сделать так, чтобы он не накладывался на основной рисунок, задать параметры заливки и текста.

Как можно видеть на примере, подписи в легенде дублируют столбец исходных данных и в таком виде представляют мало интереса.

«Оживить» легенду можно, выделив блок щелчком правой клавиши мыши и зайдя в контекстном меню Excel в подраздел «Выбрать данные».

В новом окне пользователь сможет заменить названия и значения строк и столбцов.

Чтобы придать диаграмме в Экселе приемлемый вид, следует, на время закрыв окно, добавить к таблице ещё один столбец с желаемыми наименованиями рядов данных для блока легенды.

Далее — снова открыв окно, нажать на кнопку «Изменить» в разделе «Подписи горизонтальной оси».

И выбрать, кликнув по обращённой вверх стрелочке в следующем окошке, вновь созданный столбец с названиями, после чего нажать на «ОК».

Ещё раз подтвердив свой выбор в главном окне, юзер закончит изменение подписей легенды.

Теперь блок приобрёл приятный, легко воспринимаемый читателем вид. Убрать блок с поля диаграммы можно, сняв галочку в чекбоксе или воспользовавшись клавишей Delete.

Подписи данных

Легенда позволяет понять соответствие секторов и рядов данных. С нею читать диаграмму, созданную в Excel, становится значительно проще — но ещё лучше будет подписать каждый сектор, разместив на изображении абсолютные или долевые значения, указанные в таблице.

Чтобы добавить на диаграмму, гистограмму или график подписи данных, нужно:

С помощью уже на раз упомянутого «плюсика» вызвать выплывающее меню и установить галочку в чекбоксе «Метки данных».

На рисунке в каждом из секторов появятся абсолютные значения, соответствующие оси ординат.

Автоматически выбранный Экселем вид не слишком эстетичен; имеет смысл сделать подписи более читаемыми, а заодно и выбрать формат представления информации. Для этого следует во вложенном списке «Метки данных» щёлкнуть по любому из предлагаемых системой вариантов.

Перейдя там же в «Дополнительные параметры», юзер сможет определить, какие именно сведения должны содержаться на изображении, отмечая соответствующие чекбоксы.

Так, включённая опция «Линия выноски» позволяет свободно перемещать текстовые поля возле секторов, сохраняя графические связи между ними.

Настройка графика в Excel.

Теперь выполним некоторые настройки нашего графика.

Название графика.

Добавить название графика очень просто. Достаточно левой кнопкой мыши несколько раз кликнуть в поле графика, которое называется «Название диаграммы».  Данное поле присутствует в области диаграммы сразу. Назовем наш график: Результаты продаж офисных стульев.

После того, как ввили нужное название, просто нажимаете в любую другую область диаграммы.

Название осей.

Для большей информативности добавим название осям. В нашем графики есть две оси. Вертикальная ось является шкалой. В нашем примере она показывает количество проданных стульев в штуках. Горизонтальная ось отражает месяца. С января по декабрь.

Если нажать на любую область диаграммы, появиться два элемента управления настройками. Конструктор и Формат в закладка, и три иконки в правом верхнем углу области диаграммы.

Нажмем на иконку Элементы диаграммы. Появиться меню. В нем ставим галочку напротив пункта Названия осей. Появиться возможность дать название обоим осям (горизонтальной и вертикальной). Справа от пункта Названия осей есть стрелочка. Если нажать на нее, открывается дополнительное меню, в котором можно выбрать конкретную ось и назвать только ее.

После того, как мы поставили галочку напротив пункта Названия осей,  у нас появились поля, в которые мы можем ввести названия. Назовем вертикальную ось — Продажи офисных стульев. шт., а горизонтальную ось — Месяца. Два раза кликаем по полю Название оси и у нас появляется возможность вводить в нее текст.

Можно переместить название оси наведя курсор мыши на рамку поля Название оси. 

Можно изменить  направление текста в названиях осей и названии самой диаграммы. Для этого нажимаем правой кнопкой мыши в любом месте диаграммы. Откроется контекстное меню в котором выбираем Формат области диаграммы. 

В правой части экрана появиться меню Формат области диаграммы. В нем выбираем Размер и свойства. После этого нажимаем левой кнопкой мыши на название элемента, который мы хотим повернуть (название оси или графика (диаграммы)). Меню Размер и свойства измениться. В нем появиться пункт Направление текста. Нажимаем на него. Появляется выпадающий список с различными вариантами направления текста. Выбираем тот вариант, который нам подходит.

Метки данных.

В Элементах диаграммы, также есть пункт Метки данных. Если поставить галочку напротив этого пункта, на кривой графика отобразятся значения, на основе которых он непосредственно построен. В нашем примере, это будут продажи офисных стульев в штуках, над соответствующими месяцами.

Если нажать на стрелочку справа от пункта Метка данных, появится дополнительное меню, в котором можно будет настроить отображение данных на графике, согласно предложенных вариантов.

Стиль и цвет диаграммы.

В пункте настроек Стили диаграммы можно настроить внешний вид диаграммы. Для этого в пункте Стиль есть готовые образцы. А в пункте Цвет можно выбрать цвет графика. Также, при изменение цвета в пункте Цвет, будут меняться цвета готовых образцов в пункте Стиль. 

Статьи посвященные диаграммам: