Расстояние от точки до точки: формулы, примеры, решения

Когда лучше всего использовать расчет расстояний между городами?

Необходимость рассчитать расстояний между городами может возникнуть у каждого. Раньше все считали вручную, отмечая расстояние на карте от одного населенного пункта к другому, сейчас же все возможно сделать за считанные секунды, используя удобный сервис представленный на нашем сайте. Так когда же может понадобиться расчет расстояний?

— Очень часто расчетом расстояния между городами пользуются водители дальнобойщики, которым предстоит длительная поездка

Как показывает статистика, именно дальнобойщики активно используют сервисы для расчета расстояний между городами, ведь им важно знать, сколько времени займет работа, каким будет предполагаемый расход топлива, в каких населенных пунктах можно остановиться и т.д. Это очень удобный способ спланировать свою рабочую неделю, ведь понимание того, сколько придется провести в пути и где можно остановиться значительно упрощает длительную поездку.
— В последнее время становится популярным путешествие в пределах страны на автомобиле

Но для того, чтоб правильно спланировать свой отдых, в том числе и расходы на топливо, нужно умело рассчитать расстояние поездки. Если вы знаете предполагаемую цену ДТ или бензина, а также расстояние, которое придется проехать, то расчет расхода топлива не составит труда. Четкое планирование путешествия – залог успешного отдыха без неожиданных трудностей.
— Также калькулятором расчета расстояний между городами могут пользоваться люди, которые отправляют посылки своим родным и близким, либо пользуются услугами компаний перевозчиков. Это позволит им посчитать примерную стоимость доставки.

Как видим, сервис расчета расстояний между городами может быть полезен многим людям.

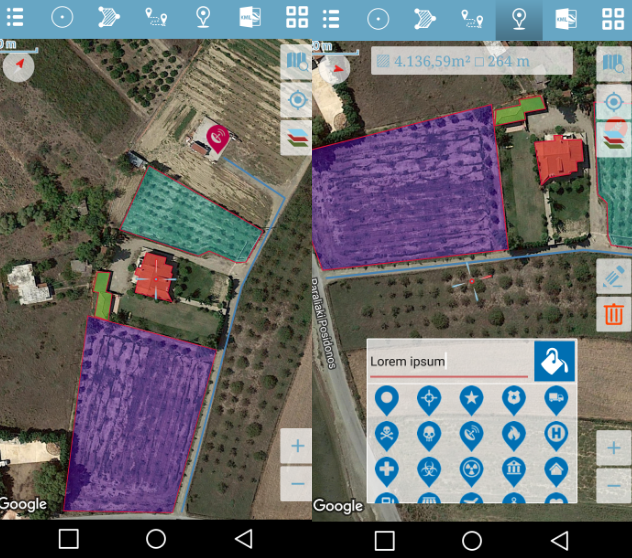
Измерение площади полей GPS

«GPS Fields Area Measure» – очень простое приложение, которое позволит вам отмечать нужные вам баллы и делиться ими с друзьями. Приложение также включает функцию, которая позволит вам отправлять автоматически сгенерированную ссылку своим друзьям в закрепленной / выбранной области.

Приложение можно бесплатно загрузить из магазина Google Play, однако оно поставляется с рекламой.

Основные характеристики:

• Регион быстрого набора
• Режим интеллектуального маркера для высокоточного размещения булавок
• Назовите, сохраните, сгруппируйте и отредактируйте меры
• Включает функцию отправки автоматически сгенерированной ссылки вашим друзьям
• Полезно для строительной площадки и строительной площадки

Вычисление расстояния шагами

Умение определять расстояния собственными шагами может пригодиться как для любителей туризма (например, при составлении схем местности и наоборот, при поиске объекта, указанного на карте или плане), так и обычным горожанам, которые занимаются, скажем, спортивной ходьбой.

Длина шага — величина постоянная

Шаги используют в качестве мерной единицы по причине того, что человек обычно делает одинаковые по длине шаги, когда идет размеренным шагом по ровной поверхности. Именно эту длину своего шага рекомендуется вычислить и запомнить, как эталонную.

На изменение эталонной длины влияет:

• усталость человека,
• температура воздуха, в жару шаги короче и скорость движения меньше,
• движение по пересеченной местности,
• ходьба в группе, когда мы интуитивно или намеренно подстраиваемся под скорость и шаг других людей,
• тяжелый рюкзак.

Способ «Мокрые ноги» Определить длину шага можно несколькими способами.

1. Способ «Мокрые ноги»

   Смысл такого измерения в том, что нужно «наследить» мокрыми ногами, затем взять рулетку и узнать расстояние от одной пятки до другой. Для чистоты расчетов, следует сделать несколько шагов, померить расстояния и вычислить среднее значение.

   Для метода подойдет любая лужа, если рядом есть сухой асфальт, можно пройти по снегу, грязи, песчаному пляжу, специально намочить ноги и прогуляться дома по полу. Главное, чтобы оставались следы от ступни.

2. Способ ходьбы на короткое расстояние Отмерьте на ровной поверхности рулеткой расстояние 10 метров. После этого пройдите и посчитайте количество шагов. Разделите 10 метров на шаги, получите длину одного шага. Затем пройдите в обратную сторону, и снова высчитайте длину шага. Вычислите среднее значение шага.
3. По карте Для данного метода подойдет карта, схема местности с объектами А и Б, находящимися в относительной близости друг от друга и расстояние между которыми легко вычислить. Идите из точки А к точке Б и считайте шаги. Разделите расстояние по полученное количество – узнаете длину собственного шага. Вместо бумажной карты можно использовать навигатор, проложив маршрут между двумя точками и затем пройдя его.
4. По росту Зная рост, также можно высчитать длину шага, однако вычисление будет слишком усредненным. Для этого рост, выраженный в сантиметрах, нужно умножить на 0,413 (для женщин) или 0,415 (для мужчин).

Имея длину шага, теперь можно без труда считать расстояния в походе или на прогулке. Интересно, что если ввести такой подсчет в привычку, то скоро вы заметите, что считаете шаги уже по инерции. Есть два способа учитывать шаги.

1. Считать каждый шаг.
2. Считать через шаг, т.е. только правую ногу или только левую. Это более удобный вариант для длительных переходов.

Как же рассчитать скорость?

На самом деле, рассчитать ее можно несколькими способами:

• через формулу нахождения мощности;
• через дифференциальные исчисления;
• по угловым параметрам и так далее.

В этой статье рассматривается самый простой способ с самой простой формулой — нахождение значения этого параметра через расстояние и время. Кстати, в формулах дифференциального расчета также присутствуют эти показатели. Формула выглядит следующим образом:

v=S/t, где

• v — скорость объекта,
• S — расстояние, которое пройдено или должно быть пройдено объектом,
• t — время, за которое пройдено или должно быть пройдено расстояние.

Как видите, в формуле первого класса средней школы нет ничего сложного. Подставив соответствующие значения вместо буквенных обозначений, можно рассчитать быстроту передвижения объекта. Например, найдем значение скорости передвижения автомобиля, если он проехал 100 км за 1 час 30 минут. Сначала требуется перевести 1 час 30 минут в часы, так как в большинстве случаев единицей измерения рассматриваемого параметра считается километр в час (км/ч). Итак, 1 час 30 минут равно 1,5 часа, потому что 30 минут есть половина или 1/2 или 0,5 часа. Сложив вместе 1 час и 0,5 часа получим 1,5 часа.

Теперь нужно подставить имеющиеся значения вместо буквенных символов:

v=100 км/1,5 ч=66,66 км/ч

Здесь v=66,66 км/ч, и это значение очень приблизительное (незнающим людям об этом лучше прочитать в специальной литературе), S=100 км, t=1,5 ч.

Таким нехитрым способом можно найти скорость через время и расстояние.

А что делать, если нужно найти среднее значение? В принципе, вычисления, показанные выше, и дают в итоге результат среднего значение искомого нами параметра. Однако можно вывести и более точное значение, если известно, что на некоторых участках по сравнению с другими скорость объекта была непостоянной. Тогда пользуются таким видом формулы:

vср=(v1+v2+v3+…+vn)/n, где v1, v2, v3, vn — значения скоростей объекта на отдельных участках пути S, n — количество этих участков, vср — средняя скорость объекта на всем протяжении всего пути.

Эту же формулу можно записать иначе, используя путь и время, за которое объект прошел этот путь:

• vср=(S1+S2+…+Sn)/t, где vср — средняя скорость объекта на всем протяжении пути,
• S1, S2, Sn — отдельные неравномерные участки всего пути,
• t — общее время, за которое объект прошел все участки.

Можно записать использовать и такой вид вычислений:

• vср=S/(t1+t2+…+tn), где S — общее пройденное расстояние,
• t1, t2, tn — время прохождения отдельных участков расстояния S.

Но можно записать эту же формулу и в более точном варианте:

vср=S1/t1+S2/t2+…+Sn/tn, где S1/t1, S2/t2, Sn/tn — формулы вычисления скорости на каждом отдельном участке всего пути S.

Таким образом, очень легко найти искомый параметр, используя данные выше формулы. Они очень просты, и как уже было указано, используются в начальных классах. Более сложные формулы базируются на этих же формулах и на тех же принципах построения и вычисления, но имеют другой, более сложный вид, больше переменных и разных коэффициентов. Это нужно для получения наиболее точного значения показателей.

Как найти расстояние, если известно время и скорость?

Чтобы найти расстояние, если известно время и скорость нужно время умножить на скорость. Пример такой задачи:

Решение задачи: Записываем в черновик, что нам известно из условия задачи:

Скорость Зайца — 1 километр за 1 минуту

Время, которое Заяц бежал до норы — 3 минуты

Расстояние — неизвестно

Теперь, то же самое запишем математическими знаками:

v — 1 км/мин

 t — 3 минуты

S — ?

Вспоминаем формулу для нахождения расстояния:

S = v ⋅ t 

Теперь запишем решение задачи цифрами:

S = 3 ⋅ 1 = 3 км

Может быть, они умеют дружить?

Как научиться решать более сложные задачи?

Чтобы научиться решать более сложные задачи нужно понять как решаются простые, запомнить какими знаками обозначаются расстояние, скорость и время. Если не получается запомнить математические формулы их нужно выписать на лист бумаги и всегда держать под рукой во время решения задач. Решайте с ребенком несложные задачи, которые можно придумать на ходу, например во время прогулки.

Ребенок, который умеет решать задачи, может гордиться собой

Единицы измерения

Когда решают задачи про скорость, время и расстояние, очень часто делают ошибку, из-за того, что забыли перевести единицы измерения.

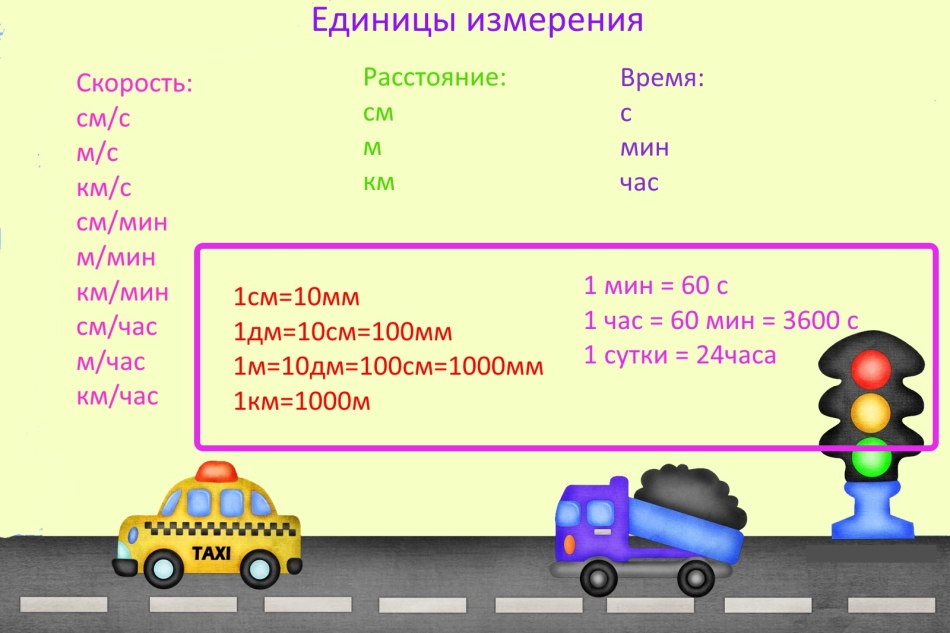
Единицы измерения для решения задач про скорость, время и расстояние

Для любознательных: Общепринятая сейчас система мер называется метрической, но так было не всегда, и в старину на Руси использовали другие единицы измерения.

Единицы измерения

Задача про удава: Слоненок и мартышка мерили длину удава шагами. Они двигались навстречу друг другу. Скорость мартышка была 60 см за одну секунду, а скорость слоненка 20 см за одну секунду. На измерение они потратили 5 секунд.  Какова длина удава? (решение под картинкой)

Как узнать длину удава?

Решение: 

Из условия задачи определяем, что нам известно скорость мартышки и слоненка и время, которое им понадобилось для измерения длины удава.

Запишем эти данные:

Скорость мартышки — 60 см/сек

Скорость слоненка — 20 см/сек

Время — 5 секунд

Расстояние неизвестно

Запишем эти данные математическими знаками:

v1 — 60 см/сек

v2 — 20 см/сек

t — 5 секунд

S — ?

Запишем формулу для расстояние, если известна скорость и время:

S = v ⋅  t 

Посчитаем, какое расстояние прошла мартышка:

S1 = 60 ⋅ 5 = 300 см

Теперь посчитаем, сколько прошел слоненок:

S2 = 20 ⋅ 5 = 100 см

Суммируем расстояние, которое прошла мартышка и расстояние, которое прошел слоненок:

S = S1 + S2 = 300 + 100 = 400 см

Включение линейки на Google Картах

Рассматриваемый онлайн-сервис и мобильное приложение предоставляют сразу несколько средств для измерения расстояния на карте

Мы не будем акцентировать внимание на дорожных маршрутах, с которыми вы можете ознакомиться в отдельной статье на нашем сайте

Вариант 1: Веб-версия

Наиболее часто используемой версией Google Карт является веб-сайт, перейти на который можно по ниже прикрепленной ниже ссылке. По желанию заранее авторизуйтесь в своем аккаунте Google, чтобы получить возможность сохранения любых выставленных отметок и многие другие функции.

1. Воспользовавшись ссылкой на главную страницу Google Maps и используя навигационные инструменты, найдите начальную точку на карте, от которой необходимо начать измерение. Для включения линейки кликните по месту правой кнопкой мыши и выберите пункт «Измерить расстояние».

После появления блока «Измерить расстояние» в нижней части окна кликните левой кнопкой мыши по следующей точке, до которой необходимо провести линию.

Для добавления дополнительных точек на линии, например, если измеряемое расстояние должно быть какой-либо специфичной формы, повторно кликните левой кнопкой мыши. За счет этого появится новая точка, а значение в блоке «Измерить расстояние» соответствующим образом обновится.

Каждую добавленную точку можно переместить, зажав ее ЛКМ. Это также относится к начальной позиции созданной линейки.

Чтобы произвести удаление одной из точек, щелкните по ней левой кнопкой мыши.

Завершить работу с линейкой можно путем щелчка по крестику в блоке «Измерить расстояние». Это действие приведет к автоматическому удалению всех выставленных точек без возможности возврата.

Настоящий веб-сервис качественно адаптирован под любые языки мира и обладает интуитивно понятным интерфейсом. Из-за этого не должно возникнуть проблем с измерением расстояния посредством линейки.

Вариант 2: Мобильное приложение

Так как мобильные устройства в отличие от компьютера доступны практически всегда, приложение Google Maps для Android и iOS также весьма популярно. В этом случае вы можете воспользоваться тем же набором функций, но в несколько ином исполнении.

1. Выполните установку приложения на странице по одной из указанных выше ссылок. В плане использования на обеих платформах ПО идентично.

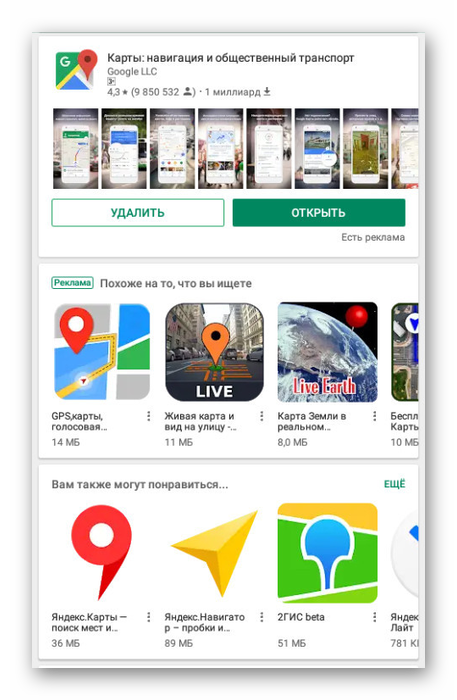
На открывшейся карте найдите начальную точку для линейки и на время зажмите. После этого на экране появится красный маркер и информационный блок с координатами.

Нажмите по названию точки в упомянутом блоке и в меню выберите пункт «Измерить расстояние».

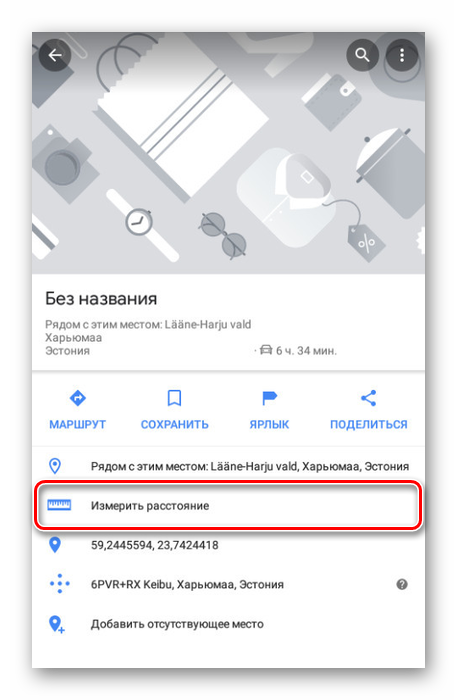
Измерение расстояния в приложении происходит в режиме реального времени и обновляется каждый раз, когда вы передвигаете карту. При этом конечная точка всегда отмечена темной иконкой и находится в центре.

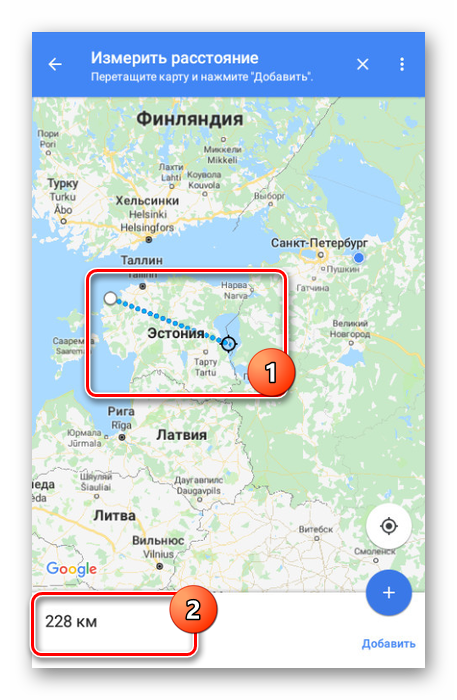
Нажмите кнопку «Добавить» на нижней панели рядом с расстоянием, чтобы зафиксировать точку и продолжить измерение без изменения уже существующей линейки.

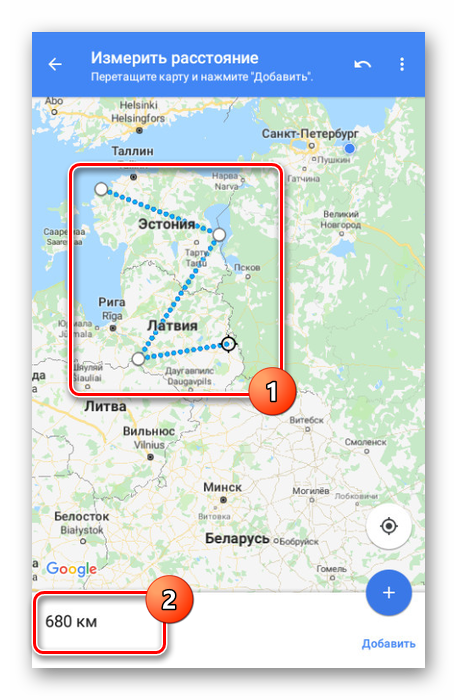
Для удаления последней точки воспользуйтесь значком с изображением стрелочки на верхней панели.

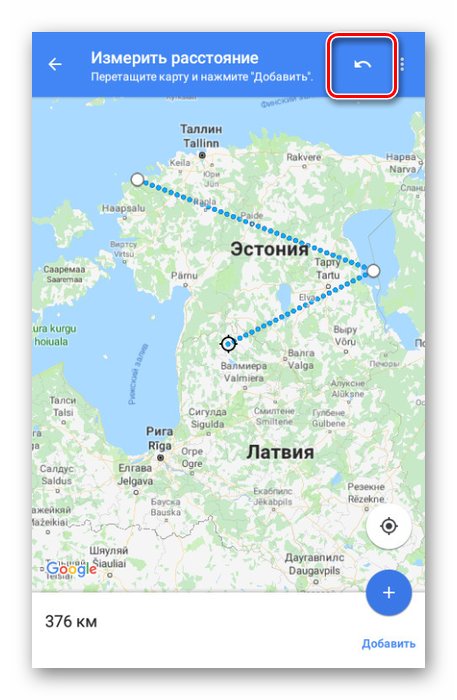
Там же можно развернуть меню и выбрать пункт «Очистить», чтобы удалить все созданные точки кроме начальной позиции.

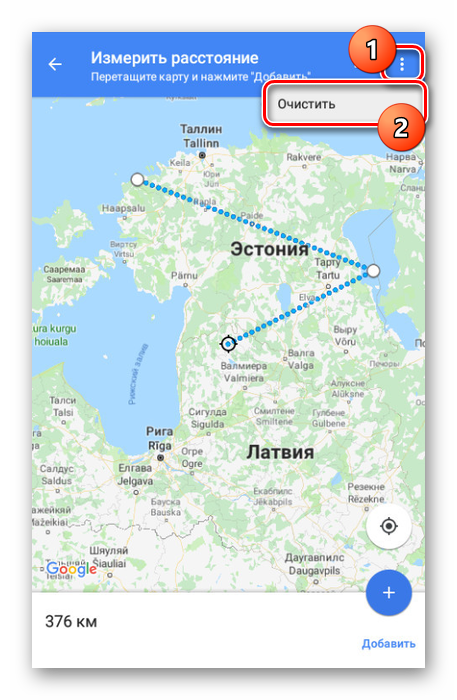
Нами были рассмотрены все аспекты работы с линейкой на Google Картах вне зависимости от версии, и потому статья подходит к завершению.

Определение расстояния «на глаз» или по линейным объектам

Метод измерения расстояния «на глаз» подходит, когда есть объект с известным размером (длина, ширина или высота). Такой расчет считается точным на 90%, а иногда и больше, если набраться опыта.

Линейные размеры самых часто встречающихся объектов:

• легковой автомобиль — Д*Ш*В соответствует 4м*1,5м*1,6м;
• взрослый человек – в среднем 1,7 м;
• голова человека – В*Ш соответствует 0,25м*0,20м;
• столб связи (деревянный) – 6 м;
• столб связи (бетонный) – 8 м;
• расстояние между столбами ЛЭП – 50 м;
• между столбами высоковольтных линий – 100 м;
• деревенский дом – 7 м;
• один этаж многоквартирного дома (панельного) – 3 м.

LКак определять стороны света в природе, рассказываю в статье: Как определить север и юг без компаса днем и ночью

Как определить расстояние до объекта

Возьмите линейку и расположите ее на уровне измеряемого объекта в 50 см от глаз. Размеры предмета (длину, ширину или высоту) измеряют по линейке и учитывают в миллиметрах.

Определение расстояния по линейке

Теперь воспользуйтесь формулой:

Расстояние, м =(реальный размер в см/измеренный размер по линейке в мм)*5.

Этот академический метод в туристической среде был немного упрощен. Определение расстояния туристы проводят по большому пальцу.

Рассмотрим на примере измерения расстояния до столба связи (высота 8 м). Длина большого пальца около 6 см. Вытяните руку перед собой, сожмите ладонь в кулак так, чтобы большой палец смотрел вверх. Расстояние от глаз до пальца будет около 60 см. Определите какой длине соответствует столб, к примеру трети пальца (2 см).

Далее осталось рассчитать пропорцию:

Х = (8 м * 60 см)/2 см =240 м.

1.2. Измерение по карте прямых и извилистых линий

Чтобы определить по карте расстояние между точками местности (предметами, объектами), пользуясь численным масштабом, надо измерить на карте расстояние между этими точками в сантиметрах и умножить полученное число на величину масштаба.

Пример, на карте масштаба 1:25000 измеряем линейкой расстояние между мостом и ветряной мельницей (рис. 2); оно равно 7,3 см, умножаем 250 м на 7,3 и получаем искомое расстояние; оно равно 1825 метров (250х7,3=1825).

Рис. 2. Определить по карте расстояние между точками местности с помощью линейки.

Небольшое расстояние между двумя точками по прямой линии проще определить, пользуясь линейным масштабом (рис. 3). Для этого достаточно циркуль-измеритель, раствор которого равен расстоянию между заданными точками на карте, приложить к линейному масштабу и снять отсчет в метрах или километрах. На рис. 3 измеренное расстояние равно 1070 м.

Рис. 3. Измерение на карте расстояний циркулем-измерителем по линейному масштабу

Рис. 4. Измерение на карте расстояний циркулем-измерителем по извилистым линиям

Большие расстояния между точками по прямым линиям измеряют обычно с помощью длинной линейки или циркуля-измерителя.

В первом случае для определения расстояния по карте с помощью линейки пользуются численным масштабом (см. рис. 2).

Во втором случае раствор «шаг» циркуля-измерителя устанавливают так, чтобы он соответствовал целому числу километров, и на измеряемом по карте отрезке откладывают целое число «шагов». Расстояние, не укладывающееся в целое число «шагов» циркуля-измерителя, определяют с помощью линейного масштаба и прибавляют к полученному числу километров.

Таким же способом измеряют расстояния по извилистым линиям (рис. 4). В этом случае «шаг» циркуля-измерителя следует брать 0,5 или 1 см в зависимости от длины и степени извилистости измеряемой линии.

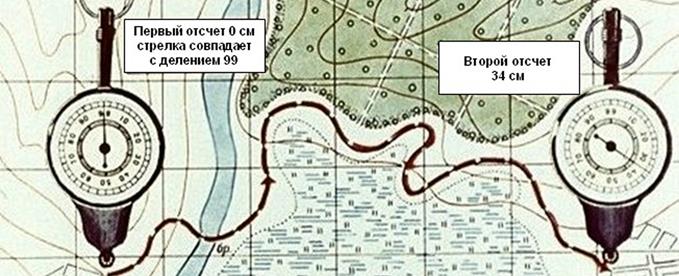Рис. 5. Измерения расстояния курвиметром

Для определения длины маршрута по карте применяют специальный прибор, называемый курвиметром (рис. 5), который особенно удобен для измерения извилистых и длинных линий.

В приборе имеется колесико, которое соединено системой передач со стрелкой.

При измерении расстояния курвиметром нужно установить его стрелку на деление 99. Держа курвиметр в вертикальном положении вести его по измеряемой линии, не отрывая от карты вдоль маршрута так, чтобы показания шкалы возрастали. Доведя до конечной точки, отсчитать измеренное расстояние и умножить его на знаменатель численного масштаба. (В данном примере 34х25000=850000, или 8500 м)

Общая формула

Скорость, время, расстояние — это 3 фундаментальных величины, связанные друг с другом. Исследуя одну характеристику, обязательно нужно учитывать две других. Фактически скорость — это физическая величина, определяющая, какую длину преодолеет физическое тело за единицу времени. Например, значение 120 км/ч показывает, что объект сможет преодолеть 120 километров за один час. В математическом виде связь между тремя характеристиками может быть записана в виде следующей формулы:

S = V * t, где:

• S — пройденное объектом расстояние;
• V — средняя скорость тела;
• t — время, затраченное на преодоление пути.

Зная это равенство и любых 2 параметра, можно выполнить расчёт третьего, так для времени она будет иметь вид t = S / V, а скорости V = S / t. Проверить правильность формулы для скорости времени и расстояния можно путём анализа размерности. Если в выражение подставить единицы измерения, то после сокращения должна получиться величина, соответствующая определяемой. S = V * t = (м / с) * с = м (метр). Что и требовалось получить. Аналогично можно проверить и 2 оставшиеся формулы: t = s / v = м / (м/с) = м * с / м = с (секунда) и V = S / t = м / с (метр на секунду).

Действительно, пусть имеется физическое тело, находящееся в каком-то месте

Через некоторое время, неважно по каким причинам, оно переместилось в другую точку, при этом не выходя за пределы установленного пространства. Если тело представить в декартовой плоскости, причём за начало принять координату (0, 0), через время объект изменит своё положение, определяющееся значением (x1, y2)

В двухмерном же пространстве это изменение можно описать как переход из точки A в Б.

Значит, чтобы тело достигло второй координаты, ему необходимо затратить время. При этом пройденный путь будет находиться в прямой зависимости от него. Расстояние и время должны связываться третьей величиной, которой как раз и является скорость. То есть параметр, определяющий, за сколько тело сможет преодолеть определённую длину.

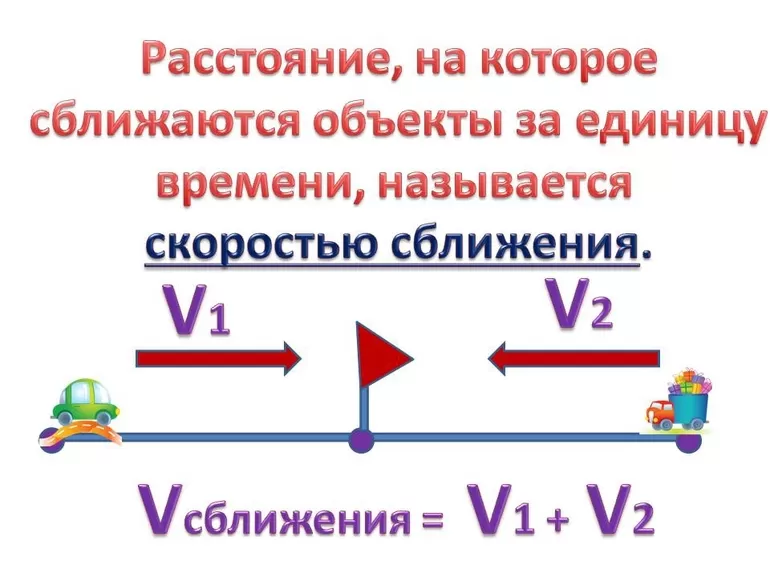
Взаимосвязь скорости, времени, расстояния

Скорость, время и расстояние связаны между собой очень крепко. Одно без другого даже сложно представить.

Если известны скорость и время движения, то можно найти расстояние. Оно равно скорости, умноженной на время: s = v × t.

Задачка 1. Мы вышли из дома и направились в гости в соседний двор. Мы дошли до соседнего двора за 15 минут. Фитнес браслет показал, что наша скорость была 50 метров в минуту. Какое расстояние мы прошли?

Как рассуждаем:

Если за одну минуту мы прошли 50 метров, то сколько таких пятьдесят метров мы пройдем за 10 минут? Умножив 50 метров на 15, мы определим расстояние от дома до магазина:

v = 50 (м/мин)

t = 15 минут

s = v × t = 50 × 15 = 750

Ответ: мы прошли 750 метров.

Если известно время и расстояние, то можно найти скорость: v = s : t.

Задачка 2. Двое школьников решили проверить, кто быстрее добежит от двора до спортплощадки. Расстояние от двора до магазина с мороженым 100 метров. Первый школьник добежал за 25 секунд. Второй за 50 секунд. Кто добежал быстрее?

Как рассуждаем:

Быстрее добежал тот, кто за 1 секунду пробежал большее расстояние. Говорят, что у него скорость движения больше. В этой задаче скорость школьников это расстояние, которое они пробегают за 1 секунду.

Чтобы найти скорость, нужно расстояние разделить на время движения. Найдем скорость первого школьника: для этого разделим 100 метров на время движения первого школьника, то есть на 25 секунд:

100 : 25 = 4

Если расстояние дано в метрах, а время движения в секундах, то скорость измеряется в метрах в секунду (м/с). Если расстояние дано в километрах, а время движения в часах, скорость измеряется в километрах в час (км/ч).

В нашей задаче расстояние дано в метрах, а время в секундах. Значит будем измерять скорость в метрах в секунду (м/с).

100 м : 25 с = 4 м/с

Так мы узнали, что скорость движения первого школьника 4 метра в секунду.

Теперь найдем скорость движения второго школьника. Для этого разделим расстояние на время движения второго школьника, то есть на 50 секунд:

100 : 50 = 2

Значит скорость движения второго школьника составляет 2 метра в секунду.

Сейчас можно сравнить скорости движения каждого школьника и узнать, кто добежал быстрее.

4 (м/с) > 2 (м/с)

Скорость первого школьника больше. Значит он добежал до магазина с мороженым быстрее.

Ответ: первый школьник добежал быстрее.

Если известна скорость и расстояние, то можно найти время: t = s : v.

Задачка 3. От школы до стадиона 500 метров. Мы должны дойти до него пешком. Наша скорость будет 100 метров в минуту. За какое время мы дойдем до стадиона из школы?

Как рассуждаем:

Если за одну минуту мы будем проходить 100 метров, то сколько таких минут со ста метрами будет в 500 метрах?

Чтобы ответить на этот вопрос нужно 500 метров разделить на расстояние, которое мы будем проходить за одну минуту, то есть на 100. Тогда мы получим время, за которое мы дойдем до стадиона:

s = 500 метров

v = 100 (м/мин)

t = s : v = 500 : 100 = 5

Ответ: от школы до стадиона мы дойдем за 5 минут.

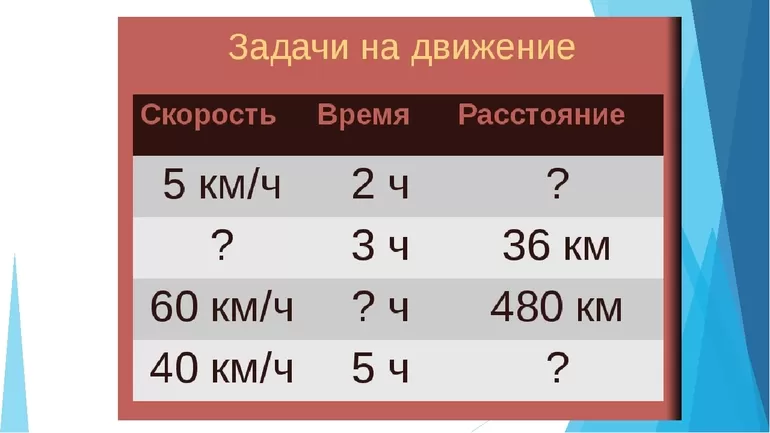
Специально для уроков математики можно распечатать или нарисовать самостоятельно такую таблицу, чтобы быстрее запомнить и применять формулы скорости, времени, расстояния.

Еще больше практики — в детской онлайн-школе Skysmart. Ученики решают примеры на интерактивной платформе: в игровом формате и с мгновенной автоматической проверкой. А еще отслеживают прогресс в личном кабинете и вдохновляются на новые свершения.

Запишите ребенка на бесплатный вводный урок математики: покажем, как все устроено и наметим индивидуальную программу, чтобы ребенок лучше учился в школе и не боялся контрольных.

Онлайн-навигатор от Яндекса

Второй навигатор онлайн, о котором мы хотим рассказать – это Яндекс.Карты. Этот сервис был основан ещё в 2004 году, и ныне только российская аудитория ресурса достигает около 25 миллионов человек. Сервис предоставляет доступ к 4 видам карт, имеется подсветка нужных географических локаций. Доступно измерений расстояния, прокладка маршрутов и просмотр панорамы улиц.

Яндекс.Карты — популярный отечественный картографический сервис

Для прокладки пути пешком с помощью Яндекс-навигатора выполните следующее:

1. Откройте Яндекс.Карты;

2. Слева вверху находится строка поиска. Справа от неё будет значок в виде змейки (Маршруты), кликните на ней;

   Нажмите на кнопку «Маршруты» сверху

3. Кликните на изображение пешехода для переключения отображения на соответствующий режим;
4. Задайте начальную и конечную точку маршрута;

5. Яндекс проложит несколько маршрутов. Выберите наиболее оптимальный из них;

   Просмотри проложенные сервисом маршруты

6. Если вы уверены, что какой-то из маршрутов неправильный, вы можете нажать на «Исправить» и предложить исправленный вариант.

   При необходимости исправьте неверный маршрут

Исправленный маршрут будет отправлен на модерацию, и, возможно, вскоре вы увидите на карте исправленный вариант.