Сложные проценты на примерах

Как рассчитать сложные проценты

Для того, чтобы просчитать, как приумножить деньги сложными процентами и какую прибыль принесет банковский вклад за несколько лет, нужно знать следующие показатели:

первоначальный размер вклада К0

ставка дохода R

количество лет, за которые нужно просчитать доход n

конечная сумма К

По следующей формуле можно рассчитать эту самую конечную прибыль: К=К0*(1+R)n А просчитав размер конечной суммы, легко можно установить размер прибыли – это разница между конечной и первоначальной суммами. При помощи приведенной выше формулы всегда можно просчитать, какой результат принесет в будущем инвестиция.

     Иногда возникают ситуации, когда нужно, наоборот, вычислить стартовую сумму вклада. Тогда эту формулу нужно преобразовать вот в такой вид: K0=K/(1+R)n С помощью формулы можно узнать и такой параметр, как процентная ставка. Эта информация требуется, когда инвестор, к примеру, хочет узнать, какую ставку ему выбрать, и на какой период нужно сделать вклад, чтобы получить конкретную прибыль. Формула вычисления сложных процентов: R=n?K/K0-1 А вот по этой формуле высчитывается период времени, на который нужно вложить средства, чтобы получить определенную желаемую прибыль: n=log1+R*K/K0

     При расчете срока вклада для получения определенной прибыли следует учитывать тот факт, что практически все банки используют целые периоды. То есть, если расчет по формуле показал, что средства для получения конкретной прибыли нужно вложить на 3 года и 9 месяцев, то нужно понимать, что в реальности необходимо будет положить депозит на 4 полных года. Есть и более сложные примеры расчетов прибыли по сложным процентам. К таким примерам относятся вклады с возможностью пополнения. Допустим, у вкладчика есть депозит, который он ежемесячно пополняет определенной суммой. Как же рассчитать, какую прибыль он получит с такого депозита?

Здесь уже простой формулой расчета не обойтись, нужны более сложные механизмы. Рассмотрим эту задачу на конкретном примере: вкладчик положил на счет 1000$ и каждый месяц добавляет к нему 50$. Допустим, процентная ставка составляет 1% в месяц. Для подсчета конечной суммы через пять лет нужно подставить в приведенные выше формулы показатели за каждый период, т.е. за 60 месяцев. Ведь сумма увеличивается не только за счет процентов, но и за счет ежемесячного добавления. При данных условиях по итогам первого месяца сумма на счету составила 1010$. К ней добавились еще 50$. То есть, для расчета конечной суммы во второй месяц процент нужно начислять уже на 1060$. И так далее, до окончания задуманного срока.

Конечно, каждый раз производить такие вычисления довольно сложно, особенно тем, кто не владеет достаточными познаниями в математике. Да и таблицы такие каждый раз не насоставляешься. Поэтому специально для вычисления сложных процентов по вкладам можно разработать свой калькулятор например в таблице excel.

Итак, очевидна разница между простыми и сложными процентами. Однако, следует отметить, что и схема простых процентов при грамотном ее использовании также может принести довольно хорошие результаты в виде прибыли. Более того, простые проценты являются единственным приемлемым вариантом, когда вкладчик нуждается в регулярном выводе средств со счета. Тогда он просто выводит сумму прибыли, накопившейся за месяц, полгода или год. Тогда как сложные проценты более приемлемы в случае долгосрочного вклада и повторного реинвестирования.

В каких случаях используется начисление простых и сложных процентов?

Формула простых процентов по вкладам применяется, когда полученные проценты плюсуются к телу депозита лишь в конце периода или совсем не прибавляются, а переводятся на другой счет. Формулу сложных процентов используют, когда проценты насчитываются через равные временные промежутки (месяц, квартал, год). Это означает проведение капитализации процентов (когда проценты насчитываются на проценты).

Простые проценты используются в случаях оформления краткосрочных вкладов, период действия которых, в основном, меньше года. Метод сложных процентов применяется при долгосрочных вкладах, которые открываются на срок больше года.

Пример сложного процента на банковском депозите

Удобно и выгодно, когда ваши деньги одномоментно задействованы в разных инструментах. Сразу рекомендую не только у менеджера устно, но и в письменном договоре детально изучить — какой именно процент используется и какие есть нюансы по нему. На некоторых банковских сайтах или в мобильных приложениях есть калькулятор сложных процентов с капитализацией и пополнением. Показываю, как работает эта формула.

1. Первоначальный вклад составил 100 тыс. рублей на 1 год с правом пополнения без ограничения суммы под 5% годовых.
2. Во втором полугодии вы добавили к вкладу еще 100 тыс. рублей.
3. За первую половину вы заработали (100000/100*5%) / 2=2500. Во втором полугодии получили (200000/100*5%) / 2 = 5000. Итого прибыль за год 7500.
4. Далее вы можете забрать свои 7500 или добавить их к 200 тыс. или увеличить вклад еще на определенную сумму.

Наиболее выгодно так работать с проверенными инструментами, поэтапно повышая сумму вклада и внося все данные в excel, чтобы не заблудиться.

 
Как правило, разница на доходе с правом неограниченного пополнения и на обычном способе не превышает 0,5-1% в год, а иногда и вовсе отсутствует.

Ради справедливости нужно рассмотреть и правило, как работает формула расчета простых процентов по кредиту, поскольку ее часто применяют в работе. Простой процент начисляется так: сумма кредита умножается на процентную ставку и поделенная на 365 дней. Для примера: у вас кредит на 100 тыс. рублей под 10% годовых. Если предложен дифференцированный способ, то ежемесячно вам будет начисляться 1000 рублей непосредственно за пользование средствами.

Оплачивая их, через определенный срок можно приступить к погашению самого «тела». Многие банки предлагают аннуитетный платеж, работающий по формуле сложного процента. Это означает, что вы будете оплачивать кредит плюс-минус равными долями. 1000 рублей в месяц за сам кредит и, например, 1000 рублей за само тело. Таким образом, уже на второй месяц проценты будут начисляться на 99 тыс. остатка и с каждым месяцем и платеж по процентам, и выплаты по кредиту будут уменьшаться.

Обратите внимание: сложные проценты по кредиту предлагаются на средних и высоких суммах, в частности, когда оформляете ипотеку или покупаете по договору автомобиль из салона. Хотя есть и аналогичные предложения среди кредитных карт, например, карта Халва, где выплаты подразумеваются равными долями за определенный период и иногда вовсе с минимальными процентами

Узнав способ начисления процента в рабочем инструменте, возможность вносить дополнительно средства или погашать кредит досрочно, важно обратить внимание еще на один аспект — ставку дисконтирования. Это величина, применяемая для пересчета грядущих денежных потоков в общую величину актуальной стоимости. С математической точки зрения, это формула, обратная сложному проценту

С ее помощью оценивается, сколько нужно сейчас инвестировать средств, чтобы, например, через 2 года, получить 100 тысяч. Рассчитывается она по формуле: итоговая сумма (100 тыс. руб) равно как произведение неизвестного на (1+0,1 (10% — средняя ставка банка)), возведенное в квадрат. Далее по правилу пропорции выделите тот самый Х (икс). Фактически, это 82644 рубля

С математической точки зрения, это формула, обратная сложному проценту. С ее помощью оценивается, сколько нужно сейчас инвестировать средств, чтобы, например, через 2 года, получить 100 тысяч. Рассчитывается она по формуле: итоговая сумма (100 тыс. руб) равно как произведение неизвестного на (1+0,1 (10% — средняя ставка банка)), возведенное в квадрат. Далее по правилу пропорции выделите тот самый Х (икс). Фактически, это 82644 рубля.

 
Учитывайте правило: ставка дисконтирования должна быть выше предложенной доходности.

В итоге подчеркну: сложные проценты в финансовых инструментах только на первый взгляд выглядят сложными, но, если разобраться в их сути, никаких камней преткновения не возникнет, а еще более — вы сможете получить существенную выгоду. Всем желаю только выгодных начислений для инвестиций и минимальных для кредита, если же вы все же решились его оформить.

Профессиональный инвестор с опытом работы 5 лет с разными финансовыми инструментами, ведет свой блог и консультирует вкладчиков. Собственные эффективные методики и информационное сопровождение инвестиций.

Формула сложного процента для банковских вкладов

На самом деле формула сложного процента применительно к банковским вкладам несколько сложнее, чем описана выше. Процентная ставка для вклада (%) рассчитывается так:

% = p * d / y

гдеp — процентная ставка (процентов годовых / 100) по вкладу,
например, если ставка 10,5%, то p = 10,5 / 100 = 0,105;d — период (количество дней), по итогам которого происходит капитализация (начисляются проценты),
например, если капитализация ежемесячная, то d = 30 дней
если капитализация раз в 3 месяца, то d = 90 дней;y — количество дней в календарном году (365 или 366).

То есть можно рассчитывать процентную ставку для различных периодов вклада.

Формула сложного процента для банковских вкладов выглядит так:

SUM = X * (1 + p*d/y)n

При расчете сложных процентов нужно принимать во внимание тот факт, что со временем наращивание денег превращается в лавину. В этом привлекательность сложных процентов

Представьте себе маленький снежный комок размером с кулак, который начал катиться со снежной горы. Пока комок катится, снег налипает на него со всех сторон и к подножию прилетит огромный снежный камень. Также и со сложным процентом. Поначалу прибавка, создаваемая сложным процентом, почти незаметна. Но через какое-то время она показывает себя во всей красе. Наглядно это можно увидеть на примере ниже.

Формулы простых и сложных процентов

Поскольку простые и сложные проценты чаще всего используются при расчете прибыли от банковских вкладов, продолжим на их примере. Для решения задач нам понадобится такая информация:

• К — начальная сумма вклада;
• К — конечная сумма вклада;
• R — ставка доходности, переводится из процентов в число (10% = 0.1);
• N — количество периодов (лет).

Формула простого процента

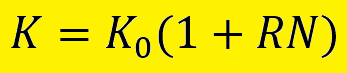
По этой формуле мы можем рассчитать конечную сумму вклада без капитализации полученной прибыли. Для этого нужно знать начальную сумму вклада, процентную ставку за 1 период инвестирования и временной интервал. Если конечная сумма задана сразу и нужно найти другую неизвестную переменную, используйте производные формулы простого процента:

Формула сложного процента

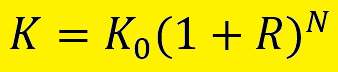
По этой формуле мы можем посчитать конечную сумму вклада с учётом капитализации полученной прибыли, зная начальный депозит, процентную ставку и нужный временной интервал. Для решения задач также можно использовать производные формулы сложного процента:

На практике часто дело не заканчивается первоначальным депозитом — многие пользуются регулярными пополнениями, например делают регулярные инвестиции из зарплаты. Для этих случаев формула сложного процента становится длиннее:

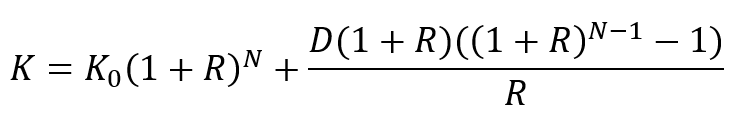
где D — сумма регулярных пополнений банковского депозита

Обратите внимание, степень N-1 означает, что доливки начинаются со второго инвестиционного периода (если сумма дополнительных инвестиций вносится сразу, то N-1 меняется на N)

Ну что, удачи на экзаменах всем читающим меня студентам 🙂 Для закрепления далее мы разберем несколько примеров задач на сложные проценты.

Формулы расчета

Раз есть сложный, значит, есть и простой процент. Несправедливо, если мы не разберем младшего брата нашего героя.

Простой процент

Простой процент каждый расчетный период (месяц, квартал, год) начисляется только на первоначальную сумму. Никакого эффекта “снежного кома” он не дает. Сумма увеличивается медленно.

Формула расчета:

S_N = S_П * (1 + % ст * N), где

• S_N – сумма в конце периода N;
• S_П – первоначальная сумма капитала;
• % ст – процентная ставка (доход);
• N – расчетный период.

Формула справедлива, если речь идет о начислении дохода раз в год. Например, положили на счет 100 000 ₽ под 10 % годовых на 10 лет. В конце срока получите: 100 000 * (1 + 0,1 * 10) = 200 000 ₽.

В реальной жизни понятие простого % применяется, например, в экономических расчетах по банковским вкладам без учета капитализации. В договоре обязательно указывается годовая процентная ставка. Проценты начисляются за каждый день нахождения денег на вкладе. А получать доход вкладчик может ежемесячно, ежеквартально или раз в год.

В этом случае формула примет вид:

S_N = S_П * (1 + % ст * Д / 365), где

Д – количество полных дней нахождения денег на депозите.

Например:

1. Положили на счет 100 000 ₽ под 10 % годовых на 91 день. В конце срока получите: 100 000 * (1 + 0,1 * 91 / 365) = 102 493,15 ₽.
2. На 180 дней: 100 000 * (1 + 0,1 * 180 / 365) = 104 931,51 ₽.
3. На 2 года (730 дней): 100 000 * (1 + 0,1 * 730 / 365) = 120 000 ₽.

Сложный процент с начислением дохода 1 раз в год

По методу сложных процентов при начислении дохода 1 раз в год будущая сумма определяется по формуле:

S_N = S_П * (1 + % ст)N

Пример. В банк положили 100 000 ₽ под 10 % годовых на 2 года. Будущая стоимость вклада составит: 100 000 * (1 + 0,1)2 = 121 000 ₽.

Сложный процент с начислением дохода чаще, чем 1 раз в год

Доход может начисляться ежемесячно, ежеквартально или 2 раза в год. Формула меняется:

S_N = S_N * (1 + % ст / К)N*К, где

К – частота начисления дохода (12, 4 или 2 раза в год).

Пример. В банк положили 100 000 ₽ под 10 % годовых на 2 года с ежемесячным начислением процентов. Будущая стоимость вклада составит: 100 000 * (1 + 0,1/12)24 = 122 039,1 ₽.

Формула для расчета

Если рассчитать размер начисленных простых процентов достаточно легко (сумму инвестированных средств умножить на ставку на количество периодов начисления), то для расчета прибыли при капитализации потребуется использовать формулу посложнее:

Н=В*(1+%)^t, где

Н – размер начисления за весь период инвестирования;

В – сумма первоначальных вложений;

% — ставка;

t – количество периодов.

При этом нужно учитывать разницу между ежегодным начислением по ставке годовых и ежемесячным начислением по ставке из расчета в годовых.

В формуле расчета сложных процентов ставка выражается в долях, а не процентах (т.е. не 12%, а 0,12). При этом нужно учитывать в расчете периодичность начисления (ежегодно, ежемесячно, непрерывно).

Сравним:

1. Александр открыл депозит на 100 000 рублей под 12% годовых на 5 лет. Начисления происходят ежегодно и капитализируются.

Н=100 000*(1+0,12)^5= 176 234

Доход Александра составит через 5 лет: 176 234 – 100 000 = 76 234 рубля.

2. Александр открыл вклад на ту же сумму, срок и под 12%, но с ежемесячным начислением. Соответственно, каждый месяц сумма, начисленная за период, будет прибавляться к сумме инвестиций и порождать новый денежный поток.

Для расчета нам необходимо разделить годовую ставку на количество периодов начисления (т.е. на 12 месяцев), а количество периодов начисления наоборот, увеличить в 12 раз.

Н=100 000*(1+0,01)^60=181 669

Прибыль Александра составит 81 669 рублей. То есть через 5 лет депозит увеличится практически в 2 раза без дополнительных вложений со стороны инвестора.

Рассчитать доход при начислении чаще одного раза в год можно путем перевода годовой ставки по инвестиционному инструменту к ежемесячной. Это делается по формуле:

%=n*t/365(366), где

n — годовая ставка,

t – количество дней в периоде (при ежемесячном начислении – 30).

В нашем случае: %=0.12*30/365=0.01

Из этих примеров также видно, что чем чаще происходит капитализация, тем больший пассивный доход можно получить. При этом чем дольше срок инвестирования, тем разительнее отличается простой и сложный процент. При дополнительных вложениях размер начисляемых процентов со времени начинает превышать дополнительные взносы.

Например, если Александр начнет докладывать на депозит по 10 000 рублей в месяц, то размер процентов по окончании срока действия вклада составит 296 609 рублей, а общая сумма на конец 5 лет составит более 977 тысяч.

Гораздо реже используется формула непрерывного начисления процентов. При t стремящемся к бесконечности формула приобретает вид:

H=B*e^rt, где е~ 2,71828

Для расчета сложных процентов по депозиту в сети можно найти массу калькуляторов (например, на агрегаторе banki.ru) или же воспользоваться функцией БС (Будущая стоимость) в Excel.

Ключевые различия между простым интересом и сложным интересом

Ниже приведены основные различия между простым и сложным интересом:

1. Проценты, начисляемые на основную сумму за весь срок кредита, известны как простые проценты. Проценты, начисляемые как на основную сумму, так и на ранее заработанные проценты, называются сложными процентами.
2. Сложный процент дает высокую доходность по сравнению с простым процентом.
3. В Простом Проценте основное значение остается постоянным, в то время как в случае Сложного Процента Основное значение изменяется из-за эффекта сложения.
4. Темпы роста Простых процентов ниже, чем сложных процентов.
5. Расчет простого процента прост, а расчет сложного процента сложен.

пример

Предположим, Алекс депонировал рупий. 1000 в банк под 5% годовых (простой и составной) в год на 3 года. Узнайте общий интерес, который он получит в конце третьего года?

Решение : здесь P = 1000, r = 5% и t = 3 года

Простой интерес =

Сложный процент =

Заключение

Проценты — это плата за использование чужих денег. Существует много причин для выплаты процентов, таких как временная стоимость денег, инфляция, альтернативные издержки и фактор риска. Простой процент быстро рассчитывается, но сложный процент практически сложен. Если вы рассчитываете как простой процент, так и сложный процент для данного принципала, ставки и времени, вы всегда обнаружите, что сложный процент всегда выше, чем простой процент из-за сложного эффекта на него.

Понятие простых процентов и как они рассчитываются

Простые проценты – это проценты, начисляющиеся лишь на первоначальную величину вклада, независимо от количества периодов и их продолжительности. Они считаются один раз по окончанию срока депозита. Это обозначает, что сумма процентов за предыдущий период не учитывается при расчете в следующем. 

Метод расчета простых процентов основан на принципе наращения денег по арифметической прогрессии. Допустим, инвестор в начале года положил в банк депозит на сумму 100 000 руб. под 10% годовых:

• через год он получит сумму, равную первоначально внесенным деньгам плюс начисленные проценты: 100 000 + 10 000 (чтобы высчитать процент нужно сумму вклада умножить на ставку и разделить на 100) = 110 000 (руб.);
• через 2 года сумма составит: 100 000 + (10 000 х 2) = 120 000 (руб.);
• через N лет вкладчик получит: 100 000 + (10 000 х N).

Поскольку банки указывают ставку за год, то чтобы определить доход за другой период (к примеру, 3 месяца), применяя простую ставку процентов, формула будет такой:

S = (P x I x Т / K) / 100, где:

S– сумма насчитанных процентов (руб.);

P– начальная сумма вложенных средств;

I– процентная ставка за год;

Т – срок действия вклада в днях;

K– число дней в году.

То есть при вкладе 100 000 руб. на 3 месяца под 10% годовыхвычисление простых процентовбудет выполняться так:

(100 000 х 10 х 92 / 365) / 100 = 2520,55 (руб.).

Получается, что в конце срока вкладчик получит на руки внесенные 100 000 руб. плюс 2520,55 руб. дохода, т.е. 102 520,55 руб.

Это интересно: Обязанности таможенного брокера, кто это такой

Простой расчет сложных процентов

Представим ситуацию — вы решили открыть депозит в банке, положив туда часть прибыли, что получили, занимаясь трейдингом на Санкт-Петербургской бирже самостоятельно или на доверительной основе через брокера. Самый простой способ расчета прибыли, полученной через сложные проценты в банковском депозите поэтапно, выглядит так:

1. Открыли вклад на 10 тысяч рублей под 5% годовых.
2. Через 365 дней прибыль составила 500 рублей.
3. Вы можете закрыть вклад, а можете его реинвестировать, добавив к нему 500 рублей прибыли и оформив договор на 10500.
4. Через год прибыль составит 525 рублей, а суммарно на счету будет 11025 р.

 
В банковской практике это принято называть капитализацией.

Формула расчета с начислением дохода 1 раз в год

Несмотря на то, что процент называют сложным, слишком сложного в нем нет ничего. Вложив в продукт, например, 100 долларов на 365 дней под 5% годовых с одноразовым начислением прибыли, на 366-ой день вы получите 105 долларов

Здесь нужно принимать во внимание еще одно правило банка — начисление процентов начинается на следующий день после открытия вклада, а вот кредит «работает» с дня заключения договора, то есть непосредственно с сегодня

Как использовать сложные проценты в инвестировании

Как вы уже знаете, получаемая от инвестиций прибыль — это важный инструмент, который на большой дистанции может во много раз увеличить доходность ваших вложений. Метод повторного вложения прибыли называется реинвестированием.

Безусловно, использовать эффект сложного процента должен каждый инвестор, однако на практике это не так просто как кажется. Существует несколько проблем, которые мешают теоретически супервыгодное реинвестирование реализовать в реальных условиях. Например, вряд ли вы слышали о людях, ставших миллиардерами через банковские депозиты. Дело в том, что деньги постоянно обесцениваются из-за инфляции — постоянного повышения цен на товары и услуги. На самом деле ставка банковских депозитов обычно примерно равна инфляции или даже ниже, поэтому реальная доходность вкладов не впечатляет:

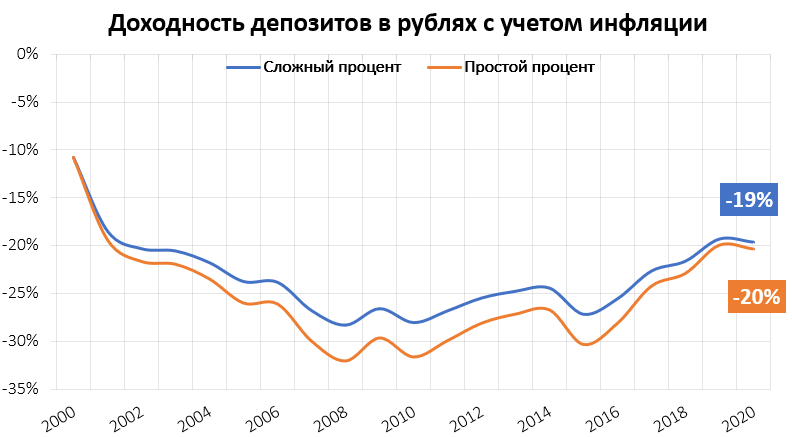
Скачать график в Excel

Даже если оставить удачный бескризисный отрезок 2010-2020 годов, доходность банковского вклада с учётом инфляции была в районе 1-2% годовых в рублях. Не говоря уже о доходности в долларах, которая после 2014 года, очевидно, находится в еще большем минусе.

Кроме инфляции сильно повлиять на итоговую доходность инвестиций могут разнообразные комиссии. Если их размер зависит от суммы инвестиций, убытки накапливаются по правилу сложных процентов, но уже с негативным эффектом. Это значит, что за несколько десятков лет инвестор может потерять сотни или даже тысячи процентов прибыли.

Такое часто встречается при инвестициях в ETF, где комиссия за управление достигает несколько процентов от депозита в год. Один из самых старых ETF под тикером SPY (инвестиционная стратегия — следование за индексом S&P 500) работает с 1993 года и берет с клиентов 0.09% в год — немного, по сравнению с другими биржевыми фондами. Эта ставка со временем может меняться, но давайте для эксперимента представим что она всегда была такой — и сравним, как будет отличаться доходность инвестиций при комиссиях от 0 до 2% в год:

Скачать график в Excel

Как видите, даже из-за несчастных 0.09% инвестор на дистанции 27 лет потерял 25% прибыли. А вроде бы небольшая комиссия в 2% годовых срезает доходность почти в 3 раза — с 723% до 270%, и это еще не учтена инфляция

По причине скрытых комиссий высокая доходность активов на самом деле может оказаться в разы ниже, поэтому перед принятием решения об инвестировании важно учитывать даже мизерные расходы

Куда же стоит инвестировать, чтобы использовать эффект сложного процента на максимум и минимизировать влияние инфляции и комиссий? Я бы выделил такие инструменты:

• Акции, в особенности американские. Сейчас это один из немногих активов, которые растут большую часть времени. Кроме того, многие компании платят дивиденды, которые можно реинвестировать и еще сильнее разгонять сложный процент. Плюс, рост цен на сами акции способен перекрыть влияние инфляции, а комиссии зависят от объема торгов, а не от вашего вклада. Взгляните на самых богатых людей планеты — почти все сделали состояние, владея большим количеством акций в своих компаниях.
• Инвестиционные фонды (в т.ч. ETF). Чаще всего это тоже инвестиции в акции, но вам не нужно самостоятельно подбирать портфель — аналитики фонда все сделают за вас. Если в портфеле фонда есть дивидендные акции, вы опять же сможете реинвестировать выплаты. При комиссии за участие ниже 1% в год катастрофического влияния на доходность ваших инвестиций не будет.
• Облигации. Обычно они дают чуть большую доходность, чем банковский депозит и способны практически без рисков приносить небольшую прибыль с учётом инфляции. В любом случае в вашем инвестиционном портфеле должны быть надёжные долгосрочные вложения, и облигации для этих целей подходят неплохо. Расходы при вложении в облигации идут на услуги фондового брокера и не зависят от общей суммы инвестиций.

Конечно, в любых инвестициях можно использовать правило сложных процентов, но не везде это рекомендуется делать. Чем выше риски вложений, тем выгоднее просто выводить прибыль, поскольку при неудачных раскладах депозит может быть потерян.

Использование сложных процентов — теоретически очень выгодное занятие, но как всегда дьявол кроется в деталях. Тем не менее, реинвестирование/капитализация остаётся одним из главных инструментов для накопления большого капитала, грех его игнорировать. И даже вне инвестирования начисление процентов по простому или сложному принципу встречается часто, поэтому полезно знать как это все работает. Надеюсь, подробный разбор формул и решения задач будут вам полезны.

Ну и подписывайтесь конечно 🙂

Удачных инвестиций и не болейте!

Что из себя представляют сложные проценты?

Сложные проценты – это проценты по депозиту или займу, учитывающие как вашу первоначальную сумму, так и проценты, накопленные этой суммой за предыдущие периоды. Поскольку вы зарабатываете проценты не только на основную сумму каждый период, но и на накопленную сумму, вы получаете больше прибыли от вложенных средств.

Со сложными процентами вы добавляете заработанные проценты обратно на свой основной баланс, и затем это приносит вам еще больше процентов, тем самым увеличивая вашу прибыль.

Допустим, у вас есть 1000 долларов на сберегательном счете, на который вы получаете 5% годовых. В первый год вы заработаете 50 долларов, в итоге ваш баланс составит 1050 долларов. Во второй год вы заработаете 5% на балансе в 1050 долларов, что составляет 52,50 доллара, что даст вам новый баланс в размере 1102,50 долларов в конце второго года.

Благодаря магии сложных процентов рост баланса вашего сберегательного счета со временем будет ускоряться, поскольку вы зарабатываете проценты на все более крупных остатках. Если вы оставите 1000 долларов на сберегательном счете на 30 лет, продолжая получать 5% годовых и никогда не добавляете ни копейки на счет, в итоге вы получите остаток в размере 4321,94 доллара.

Проценты могут быть увеличены или добавлены обратно в основную сумму в разные промежутки времени. Например, проценты могут начисляться ежегодно, ежемесячно, ежедневно или даже постоянно. Чем чаще начисляются проценты, тем быстрее растет баланс вашего счета.

Если вы начали с остатком на сберегательном счете в 1000 долларов, но заработанные вами проценты увеличивались ежедневно, а не ежегодно, через 30 лет вы получите общий баланс в размере 4481,23 доллара. Вы заработали бы дополнительно 160 долларов за счет более частого начисления процентов.

Что такое сложный процент в инвестициях простыми словами

Знание механизма расчета по депозиту позволяет вкладчикам составить прогноз дохода. Этот расчет доступен при заключении соглашений, выполнении транзакций, перед начислением вознаграждения и капитализацией прибыли.

Банки пользуются простыми и сложными формулами.

При этом применяется фиксированная ставка, которая закрепляется договором при размещении депозита, может регулироваться в случаях:

• автоматической пролонгации договора;
• досрочного закрытия.

Плавающий тип может меняться на протяжении действия соглашения.

Изменение ставок в этом случае привязано к таким факторам:

• курсу валют;
• переводу депозита в другую категорию.

При расчете дохода учитывается ряд показателей:

• инвестиционная сумма;
• процентная ставка, ее тип;
• периодичность начислений;
• срок договора.

При использовании простой схемы расчета итог получается в результате таких математических действий. Начальная сумма умножается на годовую ставку и количество дней начисления вознаграждения и делится на количество дней по календарю и на 100.

Зачем инвестировать под сложный процент

При инвестировании денег рекомендуется выбрать оптимальный вариант, который позволит использовать преимущества сложных ставок. Вложению денег всегда предшествует планирование, анализ поставленной задачи. Капитализация прибыли от инвестирования на счет позволяет получить дополнительный доход.

Простой расчет

Эффективной ставкой считается номинальный процент, который начисляется на сумму с капитализацией. Рассчитать доход можно в программе Excel. Для этого следует ввести исходные данные, формулы на базовый депозит, сумму с капитализацией. Действия выполняются автоматически, поэтому для получения корректного результата рекомендуется внимательно ввести информацию.

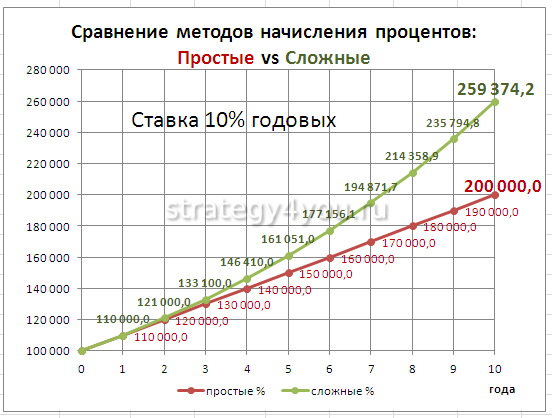
Формула

Плата за пользование средствами финансовым учреждением начисляется ежемесячно. Если вкладчик не будет снимать эти средства со счета, то они дополнят сумму основного депозита.

Формула сложного процента записывается: S=X*(1+%)n, где

• S — конечная сумма;
• X — начальный вклад;
• % — годовая ставка;
• n — количество периодов.

В результате прибыль добавляется к сумме и дает доход. Сложный расчет может действовать при открытии .

Выбирая программное предложение банка, нужно ориентироваться на итоговый доход в денежном выражении, который получится при размещении средств.