Параллельная сортировка методом пузырька на cuda

How Bubble Sort Works?

We take an unsorted array for our example. Bubble sort takes Ο(n2) time so we’re keeping it short and precise.

Bubble sort starts with very first two elements, comparing them to check which one is greater.

In this case, value 33 is greater than 14, so it is already in sorted locations. Next, we compare 33 with 27.

We find that 27 is smaller than 33 and these two values must be swapped.

The new array should look like this −

Next we compare 33 and 35. We find that both are in already sorted positions.

Then we move to the next two values, 35 and 10.

We know then that 10 is smaller 35. Hence they are not sorted.

We swap these values. We find that we have reached the end of the array. After one iteration, the array should look like this −

To be precise, we are now showing how an array should look like after each iteration. After the second iteration, it should look like this −

Notice that after each iteration, at least one value moves at the end.

And when there’s no swap required, bubble sorts learns that an array is completely sorted.

Now we should look into some practical aspects of bubble sort.

Optimized Bubble Sort Algorithm

By default, the algorithm for bubble sort in Python compares all items in the list regardless of whether the list is already sorted or not. If the given list is already sorted, comparing all values is a waste of time and resources.

Optimizing the bubble sort helps us to avoid unnecessary iterations and save time and resources.

For example, if the first and second items are already sorted, then there is no need to iterate through the rest of the values. The iteration is terminated, and the next one is initiated until the process is completed as shown in the below Bubble Sort example.

Optimization is done using the following steps

Step 1) Create a flag variable that monitors if any swapping has occurred in the inner loop

Step 2) If the values have swapped positions, continue to the next iteration

Step 3) If the benefits have not swapped positions, terminate the inner loop, and continue with the outer loop.

An optimized bubble sort is more efficient as it only executes the necessary steps and skips those that are not required.

Параметр key

Функций и sorted() содержат параметр key чтобы указать функцию вызываемую для каждого аргумента перед сравнением.

Пример регистронезависимого сравнения:

>>> sorted(«This is a test string from Andrew».split(), key=str.lower)

1 2	>>>sorted(«This is a test string from Andrew».split(),key=str.lower) ‘a’,’Andrew’,’from’,’is’,’string’,’test’,’This’

Функция передаваемая в key содержит один аргумент и возвращает ключ используемый для сортировки. Это эффективный подход, так как функция вызывается ровно один раз для каждого элемента.

Общий шаблон для отсортировки сложных объектов — использование одного из индексов как ключа:

>>> student_tuples =
>>> sorted(student_tuples, key=lambda student: student) # сортировка по возрасту

1 2 3 4 5 6 7

>>>student_tuples= …(‘john’,’A’,15), …(‘jane’,’B’,12), …(‘dave’,’B’,10), >>>sorted(student_tuples,key=lambda studentstudent2)# сортировка по возрасту (‘dave’,’B’,10),(‘jane’,’B’,12),(‘john’,’A’,15)

Тот же способ работает для объектов с именованными атрибутам:

>>> class Student:
… def __init__(self, name, grade, age):
… self.name = name
… self.grade = grade
… self.age = age
… def __repr__(self):
… return repr((self.name, self.grade, self.age))

1 2 3 4 5 6 7

>>>classStudent …def __init__(self,name,grade,age) …self.name=name …self.grade=grade …self.age=age …def __repr__(self) …returnrepr((self.name,self.grade,self.age))

>>> student_objects =
>>> sorted(student_objects, key=lambda student: student.age) # сортировка по возрасту

1 2 3 4 5 6 7

>>>student_objects= …Student(‘john’,’A’,15), …Student(‘jane’,’B’,12), …Student(‘dave’,’B’,10), >>>sorted(student_objects,key=lambda studentstudent.age)# сортировка по возрасту (‘dave’,’B’,10),(‘jane’,’B’,12),(‘john’,’A’,15)

Implementing the Bubble Sort Algorithm

We will breakdown the implementation into three (3) steps, namely the problem, the solution, and the algorithm that we can use to write code for any language.

The problem

A list of items is given in random order, and we would like to arrange the items in an orderly manner

Consider the following list:

The solution

Iterate through the list comparing two adjacent elements and swapping them if the first value is higher than the second value.

The result should be as follows:

Algorithm

The bubble sort algorithm works as follows

Step 1) Get the total number of elements. Get the total number of items in the given list

Step 2) Determine the number of outer passes (n — 1) to be done. Its length is list minus one

Step 3) Perform inner passes (n — 1) times for outer pass 1. Get the first element value and compare it with the second value. If the second value is less than the first value, then swap the positions

Step 4) Repeat step 3 passes until you reach the outer pass (n — 1). Get the next element in the list then repeat the process that was performed in step 3 until all the values have been placed in their correct ascending order.

Step 5) Return the result when all passes have been done. Return the results of the sorted list

Step 6) Optimize Algorithm

Avoid unnecessary inner passes if the list or adjacent values are already sorted. For example, if the provided list already contains elements that have been sorted in ascending order, then we can break the loop early.

Complexity Analysis of Bubble Sort

There are three types of Complexity are:

1) Sort complexity

The sort complexity is used to express the amount of execution times and space that it takes to sort the list. The bubble sort makes (n – 1) iterations to sort the list where n is the total number of elements in the list.

2) Time complexity

The time complexity of the bubble sort is O(n2)

The time complexities can be categorized as:

• Worst case – this is where the list provided is in descending order. The algorithm performs the maximum number of executions which is expressed as O(n2)
• Best case – this occurs when the provided list is already sorted. The algorithm performs the minimum number of executions which is expressed as ?(n)
• Average case – this occurs when the list is in random order. The average Complexity is represented as ?(n2)

3) Space complexity

The space complexity measures the amount of extra space that is needed for sorting the list. The bubble sort only requires one (1) extra space for the temporal variable used for swapping values. Therefore, it has a space complexity of O (1).

Summary

• The bubble sort algorithm works by comparing two adjacent values and swapping them if the value on the left is less than the value on the right.
• Implementing a bubble sort algorithm is relatively straight forward with Python. All you need to use are for loops and if statements.
• The problem that the bubble sort algorithm solves is taking a random list of items and turning it into an ordered list.
• The bubble sort algorithm in data structure performs best when the list is already sorted as it performs a minimal number of iterations.
• The bubble sort algorithm does not perform well when the list is in reverse order.
• The bubbler sort has a time complexity of O (n2) and a space complexity of O (1)
• The bubbler sort algorithm is best suited for academic purposes and not real-world applications.
• The optimized bubble sort makes the algorithm more efficient by skipping unnecessary iterations when checking values that have already been sorted.

Работа сортировки вставки в Python

Чтобы понять сортировку вставки в Python, мы взяли для нашего примера несортированный список .

Сортировка вставки сравнивает первые два элемента.

Он обнаруживает, что и 14, и 33 уже находятся в порядке возрастания. На данный момент 14 находится в отсортированном подсписке.

Сортировка вставки продвигается вперед и сравнивает 33 с 27.

И обнаруживает, что 33 находится не в правильном положении.

Он меняет 33 на 27. Он также проверяет все элементы отсортированного подсписка. Здесь мы видим, что сортированный подсписок имеет только один элемент 14, а 27 больше 14. Следовательно, сортированный подсписок остается отсортированным после замены.

К настоящему времени у нас есть 14 и 27 в отсортированном подсписке. Затем он сравнивает 33 с 10.

Эти значения не упорядочены.

Поэтому мы меняем местами элементы списка.

Однако свопинг делает 27 и 10 несортированными.

Следовательно, мы тоже меняем их местами.

Снова мы находим 14 и 10 в несортированном порядке.

Мы снова меняем их местами. К концу третьей итерации у нас есть сортированный подсписок из 4 пунктов.

Этот процесс продолжается до тех пор, пока все несортированные значения не будут покрыты отсортированным подсписком. Теперь мы рассмотрим некоторые аспекты программирования типа вставки.

Важность сортировки алгоритмов

Что такое сортировка? И почему это так важно? Это вопросы, которые мы постараемся ответить в этом разделе. Из книг в библиотеке и словах в словаре к записям базы данных и инструкции в процессоре мы испытали сортировку много раз

Из книг в библиотеке и словах в словаре к записям базы данных и инструкции в процессоре мы испытали сортировку много раз.

« в информатике, сортировка – это акт организации вещей в упорядоченной последовательности ». – Википедия

Это означает, что когда мы сортируем вещи, нам нужно знать критерии, на которые мы будем организовать последовательность, переданную нам. Для целей настоящего Учебника мы будем предполагать, что критерии – это значение числа, и мы сортируем заданную последовательность чисел.

В информатике наиболее важной целью сортировки состоит в том, чтобы произвести эффективные алгоритмы. Двоичный поиск – исключительно быстрый алгоритм поиска, который не будет возможно в несортированной коллекции объектов

Почти все установленные операции работают очень быстро на сортировке данных.

Помимо эффективных алгоритмов, сортировка используется, когда очень требование программы сортируется что-то, как программа, которая работает с палубой карт. Следовательно, алгоритмы сортировки являются одним из самых фундаментальных концепций, который должен знать программист.

Сортировка массива из случайных чисел методом пузырька

Массив называется отсортированным по возрастанию, если для любых его элементов выполняется
условие a<a. Массив называется отсортированным по убыванию, если для любых его элементов выполняется условие a>a.

Существует множество методов сортировки. Одни из них являются более эффективными, другие
проще для понимания. Достаточно простой для понимания является сортировка методом пузырька, который
также называют методом простого обмена. В чем же он заключается, и почему у него такое странное
название: «метод пузырька»?

Как известно воздух легче воды, поэтому пузырьки воздуха всплывают. Это просто аналогия. В
сортировке методом пузырька по возрастанию более легкие (с меньшим значением) элементы постепенно
«всплывают» в начало массива, а более тяжелые друг за другом опускаются на дно (в конец массива).
Алгоритм и особенности сортировки:

1. При первом проходе по массиву элементы попарно сравниваются между собой: первый со вторым, затем второй с третьим, следом третий с четвертым и т.д. Если предшествующий элемент оказывается больше последующего, то их меняют местами.
2. Не трудно догадаться, что постепенно самое большое число оказывается последним. Остальная часть массива остается не отсортированной, хотя некоторое перемещение элементов с меньшим значением в начало массива наблюдается.
3. При втором проходе незачем сравнивать последний элемент с предпоследним. Последний элемент уже стоит на своем месте. Значит, число сравнений будет на одно меньше.
4. На третьем проходе уже не надо сравнивать предпоследний и третий элемент с конца. Поэтому число сравнений будет на два меньше, чем при первом проходе.
5. В конце концов, при проходе по массиву, когда остаются только два элемента, которые надо сравнить, выполняется только одно сравнение.
6. После этого первый элемент не с чем сравнивать, и, следовательно, последний проход по массиву не нужен. Другими словами, количество проходов по массиву равно n-1, где n – это количество элементов массива.
7. Количество сравнений в каждом проходе равно n-j, где j – это номер прохода по массиву (первый, второй, третий и т.д.).
8. При обмене элементов массива обычно используется «буферная» (третья) переменная, куда временно помещается значение одного из элементов.

Delphi/Pascal

const
n = 10; { количество элементов в массиве }
var
a:array of integer;
i,j,buf:integer;
begin
{Заполняем массив случайными целыми числами от 0 до 50 и выводим массив на экран}
for i:=1 to n do
begin
a:=random(50);
write(a:3);
end;
{ сортировка массива по возрастанию }
for j:=1 to n-1 do
for i:= 1 to n-j do {проверяем все элементы до предпоследнего неотсортированного}
if a>a then { ищем элементы, которые стоят неправильно }
begin { меняем элементы местами }
buf:=a;
a:=a;
a:=buf;
end;
writeln;

writeln(‘Массив после сортировки: ‘);
for i:=1 to n do write(a,’ ‘);
end.

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26

const n=10;{количествоэлементоввмассиве} var aarray1..nofinteger; i,j,bufinteger; begin {Заполняеммассивслучайнымицелымичисламиотдо50ивыводиммассивнаэкран} fori:=1tondo begin ai=random(50); write(ai3); end; {сортировкамассиваповозрастанию} forj:=1ton-1do fori=1ton-jdo{проверяемвсеэлементыдопредпоследнегонеотсортированного} ifai>ai+1then{ищемэлементы,которыестоятнеправильно} begin{меняемэлементыместами} buf:=ai; ai=ai+1; ai+1=buf; end; writeln; writeln(‘Массив после сортировки: ‘); fori:=1tondowrite(ai,’ ‘); end.

Количество просмотров: 4 642

| Категория: Pascal | Тэги: сортировка

Анализ

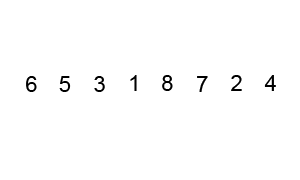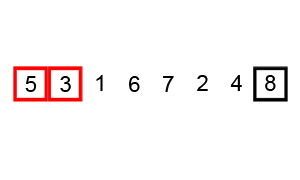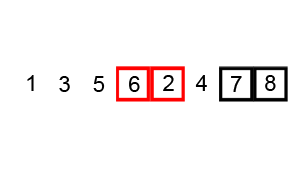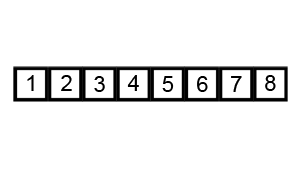
Пример пузырьковой сортировки. Начиная с начала списка, сравните каждую соседнюю пару, поменяйте их местами, если они не в правильном порядке (последняя меньше первой). После каждой итерации необходимо сравнивать на один элемент меньше (последний), пока не останется больше элементов для сравнения.

Представление

Пузырьковая сортировка имеет наихудший случай и среднюю сложность О ( n 2 ), где n — количество сортируемых элементов. Большинство практических алгоритмов сортировки имеют существенно лучшую сложность в худшем случае или в среднем, часто O ( n  log  n ). Даже другое О ( п 2 ) алгоритмы сортировки, такие как вставки рода , как правило , не работать быстрее , чем пузырьковой сортировки, а не более сложным. Следовательно, пузырьковая сортировка не является практическим алгоритмом сортировки.

Единственное существенное преимущество пузырьковой сортировки перед большинством других алгоритмов, даже быстрой сортировкой , но не сортировкой вставкой , заключается в том, что в алгоритм встроена способность определять, что список сортируется эффективно. Когда список уже отсортирован (в лучшем случае), сложность пузырьковой сортировки составляет всего O ( n ). Напротив, большинство других алгоритмов, даже с лучшей средней сложностью , выполняют весь процесс сортировки на множестве и, следовательно, являются более сложными. Однако сортировка вставкой не только разделяет это преимущество, но также лучше работает со списком, который существенно отсортирован (имеет небольшое количество инверсий ). Кроме того, если такое поведение желательно, его можно тривиально добавить к любому другому алгоритму, проверив список перед запуском алгоритма.

В случае больших коллекций следует избегать пузырьковой сортировки. Это не будет эффективно в случае коллекции с обратным порядком.

Кролики и черепахи

Расстояние и направление, в котором элементы должны перемещаться во время сортировки, определяют производительность пузырьковой сортировки, поскольку элементы перемещаются в разных направлениях с разной скоростью. Элемент, который должен двигаться к концу списка, может перемещаться быстро, потому что он может принимать участие в последовательных заменах. Например, самый большой элемент в списке будет выигрывать при каждом обмене, поэтому он перемещается в свою отсортированную позицию на первом проходе, даже если он начинается с начала. С другой стороны, элемент, который должен двигаться к началу списка, не может двигаться быстрее, чем один шаг за проход, поэтому элементы перемещаются к началу очень медленно. Если наименьший элемент находится в конце списка, потребуется n −1 проход, чтобы переместить его в начало. Это привело к тому, что эти типы элементов были названы кроликами и черепахами соответственно в честь персонажей басни Эзопа о Черепахе и Зайце .

Были предприняты различные попытки уничтожить черепах, чтобы повысить скорость сортировки пузырей. Сортировка коктейлей — это двунаправленная сортировка пузырьков, которая идет от начала до конца, а затем меняет свое направление, идя от конца к началу. Он может довольно хорошо перемещать черепах, но сохраняет сложность наихудшего случая O (n 2 ) . Комбинированная сортировка сравнивает элементы, разделенные большими промежутками, и может очень быстро перемещать черепах, прежде чем переходить к все меньшим и меньшим промежуткам, чтобы сгладить список. Его средняя скорость сопоставима с более быстрыми алгоритмами вроде быстрой сортировки .

Пошаговый пример

Возьмите массив чисел «5 1 4 2 8» и отсортируйте его от наименьшего числа к наибольшему, используя пузырьковую сортировку. На каждом этапе сравниваются элементы, выделенные жирным шрифтом . Потребуется три прохода;

Первый проход

( 5 1 4 2 8) → ( 1 5 4 2 8). Здесь алгоритм сравнивает первые два элемента и меняет местами, поскольку 5> 1.

(1 5 4 2 8) → (1 4 5 2 8), поменять местами, поскольку 5> 4

(1 4 5 2 8) → (1 4 2 5 8), поменять местами, поскольку 5> 2

(1 4 2 5 8 ) → (1 4 2 5 8 ). Теперь, поскольку эти элементы уже упорядочены (8> 5), алгоритм не меняет их местами.

Второй проход

( 1 4 2 5 8) → ( 1 4 2 5 8)

(1 4 2 5 8) → (1 2 4 5 8), поменять местами, поскольку 4> 2

(1 2 4 5 8) → (1 2 4 5 8)

(1 2 4 5 8 ) → (1 2 4 5 8 )

Теперь массив уже отсортирован, но алгоритм не знает, завершился ли он. Алгоритму требуется один дополнительный полный проход без какой-либо подкачки, чтобы знать, что он отсортирован.

Третий проход

( 1 2 4 5 8) → ( 1 2 4 5 8)

(1 2 4 5 8) → (1 2 4 5 8)

(1 2 4 5 8) → (1 2 4 5 8)

(1 2 4 5 8 ) → (1 2 4 5 8 )

Использовать

Пузырьковая сортировка — алгоритм сортировки, который непрерывно просматривает список, меняя местами элементы, пока они не появятся в правильном порядке. Список был построен в декартовой системе координат, где каждая точка ( x , y ) указывает, что значение y хранится в индексе x . Затем список будет отсортирован пузырьковой сортировкой по значению каждого пикселя

Обратите внимание, что сначала сортируется самый большой конец, а меньшим элементам требуется больше времени, чтобы переместиться в правильное положение

Хотя пузырьковая сортировка является одним из простейших алгоритмов сортировки для понимания и реализации, ее сложность O ( n 2 ) означает, что ее эффективность резко снижается в списках из более чем небольшого числа элементов. Даже среди простых алгоритмов сортировки O ( n 2 ) такие алгоритмы, как сортировка вставкой , обычно значительно более эффективны.

Из-за своей простоты пузырьковая сортировка часто используется для ознакомления с концепцией алгоритма или алгоритма сортировки для начинающих студентов- информатиков . Тем не менее, некоторые исследователи, такие как Оуэн Астрахан , пошли на многое, чтобы осудить пузырьковую сортировку и ее неизменную популярность в образовании по информатике, рекомендуя даже не преподавать ее.

Жаргон Файл , который лихо звонков bogosort «архетипический извращенно ужасный алгоритм», также вызывает пузырьковую сортировку «общий плохой алгоритм». Дональд Кнут в своей книге «Искусство компьютерного программирования» пришел к выводу, что «пузырьковая сортировка, кажется, не имеет ничего, что могло бы ее рекомендовать, кроме броского названия и того факта, что она приводит к некоторым интересным теоретическим проблемам», некоторые из которых он затем обсуждает.

Пузырьковая сортировка асимптотически эквивалентна по времени работы сортировке вставкой в ​​худшем случае, но эти два алгоритма сильно различаются по количеству необходимых перестановок. Экспериментальные результаты, такие как результаты Astrachan, также показали, что сортировка вставкой работает значительно лучше даже в случайных списках. По этим причинам многие современные учебники алгоритмов избегают использования алгоритма пузырьковой сортировки в пользу сортировки вставкой.

Пузырьковая сортировка также плохо взаимодействует с современным оборудованием ЦП. Он производит как минимум вдвое больше записей, чем сортировка вставкой, вдвое больше промахов в кеш и асимптотически больше ошибочных прогнозов переходов . Эксперименты с сортировкой строк Astrachan в Java показывают, что пузырьковая сортировка примерно в пять раз быстрее сортировки вставкой и на 70% быстрее сортировки по выбору .

В компьютерной графике пузырьковая сортировка популярна благодаря своей способности обнаруживать очень маленькую ошибку (например, замену всего двух элементов) в почти отсортированных массивах и исправлять ее с линейной сложностью (2 n ). Например, он используется в алгоритме заполнения многоугольника, где ограничивающие линии сортируются по их координате x в определенной строке сканирования (линия, параллельная оси x ), а с увеличением y их порядок изменяется (два элемента меняются местами) только при пересечения двух линий. Пузырьковая сортировка — это стабильный алгоритм сортировки, как и сортировка вставкой.

Декорируем-сортируем-раздекорируем

1. Сначала исходный список пополняется новыми значениями, контролирующими порядок сортировки.
2. Затем новый список сортируется.
3. После этого добавленные значения убираются, и в итоге остаётся отсортированный список, содержащий только исходные элементы.

Вот так можно отсортировать данные учеников по оценке:

Это работает из-за того, что кортежи сравниваются лексикографически, сравниваются первые элементы, а если они совпадают, то сравниваются вторые и так далее.

Не всегда обязательно включать индекс в декорируемый список, но у него есть преимущества:

1. Сортировка стабильна — если у двух элементов одинаковый ключ, то их порядок не изменится.
2. У исходных элементов не обязательно должна быть возможность сравнения, так как порядок декорированных кортежей будет определяться максимум по первым двум элементам. Например, исходный список может содержать комплексные числа, которые нельзя сравнивать напрямую.

Ещё эта идиома называется преобразованием Шварца в честь Рэндела Шварца, который популяризировал её среди Perl-программистов.

Для больших списков и версий Python ниже 2.4, «декорируем-сортируем-раздекорируем» будет оптимальным способом сортировки. Для версий 2.4+ ту же функциональность предоставляют функции-ключи.

7

Пузырьковая сортировка Python 3

# Оптимизированная реализация Python3

# сортировки пузырьком

# Оптимизированная версия пузырьковой сортировки

def bubbleSort(arr):

n = len(arr)

# Проход через все элементы массива

for i in range(n):

swapped = False

# Последние i элементы уже

# на месте

for j in range(0, n-i-1):

# проход через массив от 0

# n-i-1. Поменять местами элементы, если

# найденный элемент больше

# следующего

if arr > arr :

arr, arr = arr, arr

swapped = True

# Если в процессе прохода не было ни одной замены,

# то выход из функции

if swapped == False:

break

# тестирующий код

arr = 

bubbleSort(arr)

print ("Сортированный массив :")

for i in range(len(arr)):

print ("%d" %arr,end=" ")

Метод пузырька C — результат сортировки:

Сортированный массив:

11 12 22 25 34 64 90

Худшая и средняя сложность времени: O (n * n). Наихудший случай возникает, когда массив отсортирован по обратному адресу.

Сложность наилучшего случая: O (n). Наилучший случай возникает, когда массив уже отсортирован.

Пограничные случаи: сортировка занимает минимальное время (порядок n), когда элементы уже отсортированы.

Сортировка на месте: Да.

Стабильность: Да.

В компьютерной графике пузырьковая сортировка популярна благодаря возможности обнаруживать мелкие ошибки (например, обмен всего двух элементов) в почти отсортированных массивах и исправлять ее только с линейной сложностью (2n). Например, она используется в алгоритме заполнения полигонов, где ограничивающие линии сортируются по их координате x на определенной линии сканирования (линия, параллельная оси X), и с увеличением Y их порядок меняется (два элемента меняются местами) только на пересечениях двух линий.

Пожалуйста, оставьте свои комментарии, если захотите поделиться дополнительной информацией про алгоритм сортировки пузырьком.

Подробный разбор пузырьковой сортировки

Давайте разберем подробно как работает пузырьковая сортировка

Первая итереация (первый повтор алгоритма) меняет между собой 4 и 2 так как цифра два меньше чем четыре 2<4, повторюсь что алгоритм меняет значения между собой если, слева оно меньше чем справа. Далее происходит сверка между 4 и 3, и так как 3 меньше чем 4 (3<4) происходит обмен значениями. Потом проходит проверку между 4 и 8 и так как значение 4 меньше чем 8 то не происходит обмена, ведь уже и так всё на своих местах.

Далее сравнивается 8 и 1 и так как 1 меньше чем 8 (1<8) и оно не находиться слева то происходит обмен значениями.После это первый повтор алгоритма заканчивается, на анимации я выделил это зеленым фоном.

В итоге по окончанию работы алгоритма пузырьковой сортировки мы имеем следующий порядок числового массива: 2 3 4 1 8

и начинается второй повтор алгоритма.

Далее сравнивается 2 и 3 и так как два меньше чем три и оно находиться слева то просто идем дальше ничего не трогая. Также проверяем и 3 и 4 и тоже самое условие выполняется 3<4 и оно слева. Дальше проверяется 4 и 1 и тут мы видим что число 1<4 и не находиться слева, поэтому алгоритм меняет их местами. В крайний раз для второго повторения алгоритма проверяется 4 и 8, но тут всё в порядке, и мы дошли до конца начинаем третье повторение. Итоги для второго повторения такие : 2 3 1 4 8

Третье повторение пузырькового алгоритма начинается с сравнения 2 и 3, тут алгоритм проверяет что 2<3 и 2 находиться слева и оставляет их в покое и идет дальше. Сравнение же 3 и 1 показывает что 1 то меньше чем три, но почему то не слева и меняет их местами. Далее идет сравнение 3 и 4, тут всё в порядке и так далее до сравнения 4 и 8.

После этого получается следующий результат: 2 1 3 4 8

Как мы видим почти все цифры уже на своих местах и в порядке возрастания! Осталось только в последнем повторении пузырькового алгоритма поменять местами 2 и 1 и всё. После того как алгоритм закончил свою работу и проверил что цифры больше нельзя поменять местами он перестает работать с таким вот результатом: 1 2 3 4 8

Сложность алгоритмов

Тему сложности алгоритмов часто трудно понять многим программистам и студентам, они стараются пропускать ее. На сам деле она довольна проста. Сложность — это способ измерения того, как быстро работает программа.

Время выполнения описывает, сколько операций должен выполнить алгоритм до его завершения. Пространственная сложность — сколько места должно быть выделено для запуска. Например, если алгоритм принимает список размером n и по какой-то причине создает новый с таким же для каждого элемента в n, то требуется пространство n2 . Кроме того, иногда полезно знать устойчивость выполнения. Алгоритм стабилен, если он сохраняет исходный порядок элементов с одинаковыми значениями.

Таблица сложности алгоритмов:

Алгоритм	Пространственная сложность	Худший случай	Средний случай	Лучший случай	Стабильный
Сортировка слиянием	О (n)	O (n lоg n)	O (n log n)	O (n lоg n)	Да
Сортировка вставками	О (1)	O (n 2 )	O (n 2 )	O (n)	Да
Сортировка пузырьком	О (1)	O (n 2 )	O (n 2 )	O (n)	Да
Быстрая	lоg n	O (n 2 )	O (n log n)	O (n lоg n)	Обычно нет*
Сортировка блоками	O (1)	O (n lоg n)	O (n log n)	O (n lоg n)	Нет
Сортировка подсчетом	O (k+n)	O (k+n)	O (k+n)	O (k+n)	Да

При выборе используемого алгоритма нужно взвесить эти факторы. Например, быстрая является очень шустрой, но ее может быть довольно сложно реализовать. Пузырьковая сортировка — медленный алгоритм, но его очень легко сделать. Для небольших наборов данных может быть лучше использовать вторую, поскольку она может быть реализована не так трудно, но для больших стоит использовать быструю.

Сравнение скоростей сортировок

Для сравнения сгенерируем массив из 5000 чисел от 0 до 1000. Затем определим время, необходимое для завершения каждого алгоритма. Повторим каждый метод 10 раз, чтобы можно было более точно установить, насколько каждый из них производителен.

Пузырьковая сортировка — самый медленный из всех алгоритмов. Возможно, он будет полезен как введение в тему алгоритмов сортировки, но не подходит для практического использования.Быстрая сортировка хорошо оправдывает своё название, почти в два раза быстрее, чем сортировка слиянием, и не требуется дополнительное место для результирующего массива.Сортировка вставками выполняет меньше сравнений, чем сортировка выборкой и в реальности должна быть производительнее, но в данном эксперименте она выполняется немного медленней. Сортировка вставками делает гораздо больше обменов элементами. Если эти обмены занимают намного больше времени, чем сравнение самих элементов, то такой результат вполне закономерен.

Вы познакомились с шестью различными алгоритмами сортировок и их реализациями на Python. Масштаб сравнения и количество перестановок, которые выполняет алгоритм вместе со средой выполнения кода, будут определяющими факторами в производительности. В реальных приложениях Python рекомендуется использовать встроенные функции сортировки, поскольку они реализованы именно для удобства разработчика.

Лучше понять эти алгоритмы вам поможет их визуализация.

Перевод статьи «Sorting Algorithms in Python»

Problem statement

We are given an array (or a list) of data. We are also given a way to “order” the elements present in the data. Now, we are asked to arranged the data as per the given order. As an example, we are given an array of integers: . We are given the “order” as “smaller than”. So, we are asked to arrange the elements of this array in such a way that each element is smaller than its successor. Basically, we need to find a way to sort this array so that the final array obtained is . There are several techniques/algorithms to achieve this ordered output array. One such well-known technique that we will discuss in this blog is called Bubble Sort.

Быстрая сортировка

Этот алгоритм также относится к алгоритмам «разделяй и властвуй». Его используют чаще других алгоритмов, описанных в этой статье. При правильной конфигурации он чрезвычайно эффективен и не требует дополнительной памяти, в отличие от сортировки слиянием. Массив разделяется на две части по разные стороны от опорного элемента. В процессе сортировки элементы меньше опорного помещаются перед ним, а равные или большие —позади.

Алгоритм

Быстрая сортировка начинается с разбиения списка и выбора одного из элементов в качестве опорного. А всё остальное передвигаем так, чтобы этот элемент встал на своё место. Все элементы меньше него перемещаются влево, а равные и большие элементы перемещаются вправо.

Реализация

Существует много вариаций данного метода. Способ разбиения массива, рассмотренный здесь, соответствует схеме Хоара (создателя данного алгоритма).

Время выполнения

В среднем время выполнения быстрой сортировки составляет O(n log n).

Обратите внимание, что алгоритм быстрой сортировки будет работать медленно, если опорный элемент равен наименьшему или наибольшему элементам списка. При таких условиях, в отличие от сортировок кучей и слиянием, обе из которых имеют в худшем случае время сортировки O(n log n), быстрая сортировка в худшем случае будет выполняться O(n²)

Споры по поводу имени

Сортировку пузырьков иногда называют «сортировкой по тону».

Например, в книге Дональда Кнута « Искусство компьютерного программирования» , том 3: Сортировка и поиск, он заявляет в разделе 5.2.1 «Сортировка вставкой», что «устанавливается на свой надлежащий уровень» и что этот метод сортировки имеет иногда называют техникой просеивания или погружения .

Эта дискуссия увековечивается из-за легкости, с которой можно рассматривать этот алгоритм с двух разных, но одинаково обоснованных точек зрения:

1. Эти большие значения могут рассматриваться как более тяжелый , и поэтому видно постепенно раковине в нижней части списка
2. Эти меньшие значения можно рассматривать как легче и , следовательно , можно видеть , прогрессивно пузыриться к вершине списка.

Заключение

Метод пузырька гораздо менее эффективен других алгоритмов, однако он имеет простую и понятную реализацию, поэтому часто используется в учебных целях. Кроме того, пузырьковая сортировка может использоваться для работы с небольшими массивами данных.

На самом деле, вместо самостоятельного написания алгоритмов сортировки программисты на Python используют стандартные функции и методы языка, такие как и . Эти функции отлажены и работают быстро и эффективно.

Знания особенностей алгоритмов сортировки, их сложности и принципов реализации в общем виде пригодятся каждому программисту, желающему пройти собеседование и стать Python-разработчиком.