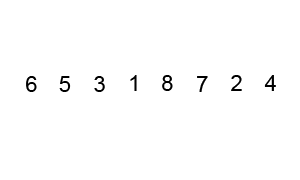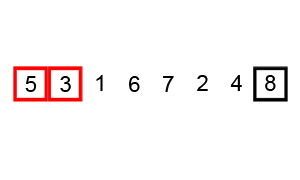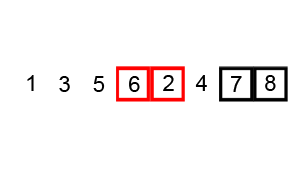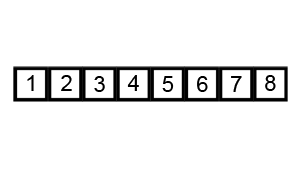Функции сортировки sort и sorted

Анализ

Пример пузырьковой сортировки. Начиная с начала списка, сравните каждую соседнюю пару, поменяйте их местами, если они не в правильном порядке (последняя меньше первой). После каждой итерации необходимо сравнивать на один элемент меньше (последний), пока не останется больше элементов для сравнения.

Представление

Пузырьковая сортировка имеет наихудший случай и среднюю сложность О ( n 2 ), где n — количество сортируемых элементов. Большинство практических алгоритмов сортировки имеют существенно лучшую сложность в худшем случае или в среднем, часто O ( n  log  n ). Даже другое О ( п 2 ) алгоритмы сортировки, такие как вставки рода , как правило , не работать быстрее , чем пузырьковой сортировки, а не более сложным. Следовательно, пузырьковая сортировка не является практическим алгоритмом сортировки.

Единственное существенное преимущество пузырьковой сортировки перед большинством других алгоритмов, даже быстрой сортировкой , но не сортировкой вставкой , заключается в том, что в алгоритм встроена способность определять, что список сортируется эффективно. Когда список уже отсортирован (в лучшем случае), сложность пузырьковой сортировки составляет всего O ( n ). Напротив, большинство других алгоритмов, даже с лучшей средней сложностью , выполняют весь процесс сортировки на множестве и, следовательно, являются более сложными. Однако сортировка вставкой не только разделяет это преимущество, но также лучше работает со списком, который существенно отсортирован (имеет небольшое количество инверсий ). Кроме того, если такое поведение желательно, его можно тривиально добавить к любому другому алгоритму, проверив список перед запуском алгоритма.

В случае больших коллекций следует избегать пузырьковой сортировки. Это не будет эффективно в случае коллекции с обратным порядком.

Кролики и черепахи

Расстояние и направление, в котором элементы должны перемещаться во время сортировки, определяют производительность пузырьковой сортировки, поскольку элементы перемещаются в разных направлениях с разной скоростью. Элемент, который должен двигаться к концу списка, может перемещаться быстро, потому что он может принимать участие в последовательных заменах. Например, самый большой элемент в списке будет выигрывать при каждом обмене, поэтому он перемещается в свою отсортированную позицию на первом проходе, даже если он начинается с начала. С другой стороны, элемент, который должен двигаться к началу списка, не может двигаться быстрее, чем один шаг за проход, поэтому элементы перемещаются к началу очень медленно. Если наименьший элемент находится в конце списка, потребуется n −1 проход, чтобы переместить его в начало. Это привело к тому, что эти типы элементов были названы кроликами и черепахами соответственно в честь персонажей басни Эзопа о Черепахе и Зайце .

Были предприняты различные попытки уничтожить черепах, чтобы повысить скорость сортировки пузырей. Сортировка коктейлей — это двунаправленная сортировка пузырьков, которая идет от начала до конца, а затем меняет свое направление, идя от конца к началу. Он может довольно хорошо перемещать черепах, но сохраняет сложность наихудшего случая O (n 2 ) . Комбинированная сортировка сравнивает элементы, разделенные большими промежутками, и может очень быстро перемещать черепах, прежде чем переходить к все меньшим и меньшим промежуткам, чтобы сгладить список. Его средняя скорость сопоставима с более быстрыми алгоритмами вроде быстрой сортировки .

Пошаговый пример

Возьмите массив чисел «5 1 4 2 8» и отсортируйте его от наименьшего числа к наибольшему, используя пузырьковую сортировку. На каждом этапе сравниваются элементы, выделенные жирным шрифтом . Потребуется три прохода;

Первый проход

( 5 1 4 2 8) → ( 1 5 4 2 8). Здесь алгоритм сравнивает первые два элемента и меняет местами, поскольку 5> 1.

(1 5 4 2 8) → (1 4 5 2 8), поменять местами, поскольку 5> 4

(1 4 5 2 8) → (1 4 2 5 8), поменять местами, поскольку 5> 2

(1 4 2 5 8 ) → (1 4 2 5 8 ). Теперь, поскольку эти элементы уже упорядочены (8> 5), алгоритм не меняет их местами.

Второй проход

( 1 4 2 5 8) → ( 1 4 2 5 8)

(1 4 2 5 8) → (1 2 4 5 8), поменять местами, поскольку 4> 2

(1 2 4 5 8) → (1 2 4 5 8)

(1 2 4 5 8 ) → (1 2 4 5 8 )

Теперь массив уже отсортирован, но алгоритм не знает, завершился ли он. Алгоритму требуется один дополнительный полный проход без какой-либо подкачки, чтобы знать, что он отсортирован.

Третий проход

( 1 2 4 5 8) → ( 1 2 4 5 8)

(1 2 4 5 8) → (1 2 4 5 8)

(1 2 4 5 8) → (1 2 4 5 8)

(1 2 4 5 8 ) → (1 2 4 5 8 )

Параметр key

Функций и sorted() содержат параметр key чтобы указать функцию вызываемую для каждого аргумента перед сравнением.

Пример регистронезависимого сравнения:

>>> sorted(«This is a test string from Andrew».split(), key=str.lower)

1 2	>>>sorted(«This is a test string from Andrew».split(),key=str.lower) ‘a’,’Andrew’,’from’,’is’,’string’,’test’,’This’

Функция передаваемая в key содержит один аргумент и возвращает ключ используемый для сортировки. Это эффективный подход, так как функция вызывается ровно один раз для каждого элемента.

Общий шаблон для отсортировки сложных объектов — использование одного из индексов как ключа:

>>> student_tuples =
>>> sorted(student_tuples, key=lambda student: student) # сортировка по возрасту

1 2 3 4 5 6 7

>>>student_tuples= …(‘john’,’A’,15), …(‘jane’,’B’,12), …(‘dave’,’B’,10), >>>sorted(student_tuples,key=lambda studentstudent2)# сортировка по возрасту (‘dave’,’B’,10),(‘jane’,’B’,12),(‘john’,’A’,15)

Тот же способ работает для объектов с именованными атрибутам:

>>> class Student:
… def __init__(self, name, grade, age):
… self.name = name
… self.grade = grade
… self.age = age
… def __repr__(self):
… return repr((self.name, self.grade, self.age))

1 2 3 4 5 6 7

>>>classStudent …def __init__(self,name,grade,age) …self.name=name …self.grade=grade …self.age=age …def __repr__(self) …returnrepr((self.name,self.grade,self.age))

>>> student_objects =
>>> sorted(student_objects, key=lambda student: student.age) # сортировка по возрасту

1 2 3 4 5 6 7

>>>student_objects= …Student(‘john’,’A’,15), …Student(‘jane’,’B’,12), …Student(‘dave’,’B’,10), >>>sorted(student_objects,key=lambda studentstudent.age)# сортировка по возрасту (‘dave’,’B’,10),(‘jane’,’B’,12),(‘john’,’A’,15)

Дополнительные заметки о сортировке в Python

Перед завершением статьи давайте рассмотрим, что говорит документация Python о сортировке:

Как видите, в официальной документации утверждается, что уже и так было доказано: немного эффективнее. Кроме того, в документации говорится о том, что зачастую намного удобнее.

Может возникнуть вопрос касательно того, являются ли обе техники стабильные. К счастью, в документации есть ответ и на это:

Также верно при использовании реверсивного параметра или применении реверсивной функции дважды.

Заключение

После проведения небольшого анализа мы доказали, что немного быстрее и потребляет на 24% меньше памяти. Однако, стоит иметь в виду, что имплементируется только для списков, в то время как принимает любые итерации. Кроме того, при использовании вы потеряете оригинальный список.

Сортировка пузырьком

Этот метод, вероятно, является первым достаточно сложным модулем, который должен написать любой начинающий программист. Это очень простая конструкция, которая знакомит учащихся с основами работы алгоритмов.

Пузырьковая (обменная) использует двумерный или одномерный массив и механизм обмена. Большинство языков программирования имеют встроенную функцию для перестановки элементов. Даже если функция обмена не существует, требуется всего пара дополнительных строк кода. Вместо перебора массива, пузырьковая работает по схеме сравнения соседних пар объектов. Шаги:

1. Если элементы расположены не в правильном порядке, они меняются местами так, что самый большой из двух перемещается вверх. Этот процесс продолжается до тех пор, пока самый большой из объектов, не окажется на первом месте.
2. После этого начинается поиск следующего по величине элемента.
3. Перестановка остановится, когда весь массив окажется в правильном порядке.

Сортировка пузырьком на Pascal (Паскаль):

Сортировка массива методом пузырька на Python (Питон):

На Java:

Из-за своей простоты этот метод часто используется для представления концепции алгоритма сортировки. В компьютерной графике она популярна благодаря своей способности выявлять очень маленькую ошибку (например, перестановку всего двух элементов) в почти отсортированных массивах и исправлять ее с помощью линейной сложности.

Какой способ обработки данных выбрать, специалист решает сам, в зависимости от времени и объема информации.

Сравнение

Пора перейти к самому интересному.
Составим список функций, которые будем сравнивать:

Разберем несколько ситуаций: оба списка примерно одинакового размера, один список большой, а второй маленький, количество вариантов элементов большое, количество вариантов маленькое. Кроме этого проведем просто общий случайный тест.

Тест первый

Проведем общий тест, размеры от до , элементы от до .

Отдельно сравним и :

тратит колоссально больше времени в общем случае, как и ожидалось.

Не будем учитывать здесь огромный , чтобы лучше видеть разницу между другими:

показал себя относительно неплохо по сравнению с ручной реализацией и .

Методы на итераторах работают еще быстрее, при этом видно, что получилось выгоднее построить генератор, чем добавлять элементы в список.

Тест второй, сравнимые размеры

Размеры будут принадлежать отрезку , а увеличиваем, начиная с . Шаг .

Как уже можно видеть при небольшом размере списков еще ведет себя как , а дальше обгоняет всех.

Тест третий, один маленький, второй большой

Размер первого равен , размер второго .

В самом начале (на очень маленьких списках) обгоняет всех, кроме , но на чуть больших все выходит на стандартные позиции.

Тест четвертый, много повторных

Размеры фиксированы, а количество элементов увеличивается на , начиная с .

Как видно, на достаточно малых количествах оказывается быстрее и , но потом он отстает.

Реализация

Сортировка массивов

Быстрая сортировка является естественным рекурсивным алгоритмом — разделите входной массив на меньшие массивы, переместите элементы в нужную сторону оси и повторите.

При этом мы будем использовать две функции — partition() и quick_sort().

Давайте начнем с функции partition():

def partition(array, begin, end):
    pivot = begin
    for i in xrange(begin+1, end+1):
        if array <= array:
            pivot += 1
            array, array = array, array
    array, array = array, array
    return pivot

И, наконец, давайте реализуем функцию quick_sort():

def quick_sort(array, begin=0, end=None):
    if end is None:
        end = len(array) - 1
    
    def _quicksort(array, begin, end):
        if begin >= end:
            return
        pivot = partition(array, begin, end)
        _quicksort(array, begin, pivot-1)
        _quicksort(array, pivot+1, end)
    return _quicksort(array, begin, end)

После того, как обе функции реализованы, мы можем запустить quick_sort():

array = 

quick_sort(array)
print(array)

Результат:

Поскольку алгоритм unstable (нестабилен), нет никакой гарантии, что два 19 будут всегда в этом порядке друг за другом. Хотя это ничего не значит для массива целых чисел.

Оптимизация быстрой сортировки

Учитывая, что быстрая сортировка сортирует «половинки» заданного массива независимо друг от друга, это оказывается очень удобным для распараллеливания. У нас может быть отдельный поток, который сортирует каждую «половину» массива, и в идеале мы могли бы вдвое сократить время, необходимое для его сортировки.

Однако быстрая сортировка может иметь очень глубокий рекурсивный стек вызовов, если нам особенно не повезло в выборе опорного элемента, а распараллеливание будет не так эффективно, как в случае сортировки слиянием.

Для сортировки небольших массивов рекомендуется использовать простой нерекурсивный алгоритм. Даже что-то простое, например сортировка вставкой, будет более эффективным для небольших массивов, чем быстрая сортировка. Поэтому в идеале мы могли бы проверить, имеет ли наш подмассив лишь небольшое количество элементов (большинство рекомендаций говорят о 10 или менее значений), и если да, то мы бы отсортировали его с помощью Insertion Sort (сортировка вставкой).

Потребление памяти при сортировке в Python

Рассмотрим подробнее наш Python скрипт:

Python

# memory_measurement/main.py

import random
import resource
import sys
import time

from sniffing import FunctionSniffingClass

def list_sort(arr):
return arr.sort()

def sorted_builtin(arr):
return sorted(arr)

if __name__ == «__main__»:
if len(sys.argv) != 2:
sys.exit(«Please run: python (sort|sorted)»)
elif sys.argv == «sorted»:
func = sorted_builtin
elif sys.argv == «sort»:
func = list_sort
else:
sys.exit(«Please run: python (sort|sorted)»)

# код теста Lib
arr =
mythread = FunctionSniffingClass(func, arr)
mythread.start()

used_mem = 0
max_memory = 0
memory_usage_refresh = .005 # Секунды

while(1):
time.sleep(memory_usage_refresh)
used_mem = (resource.getrusage(resource.RUSAGE_SELF).ru_maxrss)
if used_mem > max_memory:
max_memory = used_mem

# Проверяет, завершен ли вызов функции
if mythread.isShutdown():
# Уберите знак комментария, если вы хотите увидеть результат
# print(mythread.results)
break;

print(«\nMAX Memory Usage:», round(max_memory / (2 ** 20), 3), «MB»)

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50

# memory_measurement/main.py   importrandom importresource importsys importtime fromsniffing importFunctionSniffingClass deflist_sort(arr) returnarr.sort() defsorted_builtin(arr) returnsorted(arr) if__name__==»__main__» iflen(sys.argv)!=2 sys.exit(«Please run: python (sort|sorted)») elifsys.argv1==»sorted» func=sorted_builtin elifsys.argv1==»sort» func=list_sort else sys.exit(«Please run: python (sort|sorted)») # код теста Lib arr=random.randint(,50)forrinrange(1_000_000) mythread=FunctionSniffingClass(func,arr) mythread.start() used_mem= max_memory= memory_usage_refresh=.005# Секунды while(1) time.sleep(memory_usage_refresh) used_mem=(resource.getrusage(resource.RUSAGE_SELF).ru_maxrss) ifused_mem>max_memory max_memory=used_mem   # Проверяет, завершен ли вызов функции ifmythread.isShutdown() # Уберите знак комментария, если вы хотите увидеть результат # print(mythread.results) break; print(«\nMAX Memory Usage:»,round(max_memory(2**20),3),»MB»)

Для встроенных функций мы создаем две функции-обертки, чтобы была возможность передавать их в качестве аргументов в . Мы могли бы передать встроенную отсортированную функцию непосредственно в , но нам требуются одинаковые шансы для обеих. По этой причине мы также создадим для нее функцию-обертку. Кроме того, реализован простой синтаксический парсинг аргументов командной строки, позволяющий использовать его как можно проще из командной строки.

Интересно, как все работает? Посмотрим!

Shell

$ python memory_measurement/main.py sort
Calling the Target Function…
Function Call Complete

MAX Memory Usage: 23.371 MB

$ python memory_measurement/main.py sorted
Calling the Target Function…
Function Call Complete

MAX Memory Usage: 30.879 MB

1 2 3 4 5 6 7 8 9 10 11

$python memory_measurementmain.pysort Calling the Target Function… FunctionCall Complete MAX Memory Usage23.371MB $python memory_measurementmain.pysorted Calling the Target Function… FunctionCall Complete MAX Memory Usage30.879MB

Как видите, функция потребляет примерно на 32% больше памяти, чем метод . Этого следовало ожидать, так как последний вариант изменяет список на месте, тогда как первый всегда создают отдельный список.

Перестройка массива

После нарезки данных вам может понадобиться изменить их.

Например, некоторые библиотеки, такие как scikit-learn, могут требовать, чтобы одномерный массив выходных переменных (y) был сформирован как двумерный массив с одним столбцом и результатами для каждого столбца.

Некоторые алгоритмы, такие как рекуррентная нейронная сеть с короткой кратковременной памятью в Keras, требуют ввода данных в виде трехмерного массива, состоящего из выборок, временных шагов и функций.

Важно знать, как изменить ваши массивы NumPy, чтобы ваши данные соответствовали ожиданиям конкретных библиотек Python. Мы рассмотрим эти два примера

Форма данных

Массивы NumPy имеют атрибут shape, который возвращает кортеж длины каждого измерения массива.

Например:

При выполнении примера печатается кортеж для одного измерения.

Кортеж с двумя длинами возвращается для двумерного массива.

Выполнение примера возвращает кортеж с количеством строк и столбцов.

Вы можете использовать размер измерений вашего массива в измерении формы, например, указав параметры.

К элементам кортежа можно обращаться точно так же, как к массиву, с 0-м индексом для числа строк и 1-м индексом для количества столбцов. Например:

Запуск примера позволяет получить доступ к конкретному размеру каждого измерения.

Изменить форму 1D в 2D Array

Обычно требуется преобразовать одномерный массив в двумерный массив с одним столбцом и несколькими массивами.

NumPy предоставляет функцию reshape () для объекта массива NumPy, который можно использовать для изменения формы данных.

Функция reshape () принимает единственный аргумент, который задает новую форму массива. В случае преобразования одномерного массива в двумерный массив с одним столбцом кортеж будет иметь форму массива в качестве первого измерения (data.shape ) и 1 для второго измерения.

Собрав все это вместе, мы получим следующий проработанный пример.

При выполнении примера печатается форма одномерного массива, изменяется массив, чтобы иметь 5 строк с 1 столбцом, а затем печатается эта новая форма.

Изменить форму 2D в 3D Array

Обычно требуется преобразовать двумерные данные, где каждая строка представляет последовательность в трехмерный массив для алгоритмов, которые ожидают множество выборок за один или несколько временных шагов и одну или несколько функций.

Хорошим примером являетсямодель в библиотеке глубокого обучения Keras.

Функция изменения формы может использоваться напрямую, указывая новую размерность. Это ясно с примером, где каждая последовательность имеет несколько временных шагов с одним наблюдением (функцией) на каждый временной шаг.

Мы можем использовать размеры в атрибуте shape в массиве, чтобы указать количество выборок (строк) и столбцов (временных шагов) и зафиксировать количество объектов в 1

Собрав все это вместе, мы получим следующий проработанный пример.

При выполнении примера сначала печатается размер каждого измерения в двумерном массиве, изменяется форма массива, а затем суммируется форма нового трехмерного массива.

Key Functions

Starting with Python 2.4, both list.sort() and sorted() added a key parameter to specify a function to be called on each list element prior to making comparisons.

For example, here’s a case-insensitive string comparison:

>>> sorted("This is a test string from Andrew".split(), key=str.lower)

The value of the key parameter should be a function that takes a single argument and returns a key to use for sorting purposes. This technique is fast because the key function is called exactly once for each input record.

A common pattern is to sort complex objects using some of the object’s indices as a key. For example:

>>> student_tuples = 
>>> sorted(student_tuples, key=lambda student: student)   # sort by age

The same technique works for objects with named attributes. For example:

>>> class Student:
        def __init__(self, name, grade, age):
                self.name = name
                self.grade = grade
                self.age = age
        def __repr__(self):
                return repr((self.name, self.grade, self.age))
        def weighted_grade(self):
                return 'CBA'.index(self.grade) / float(self.age)

>>> student_objects = 
>>> sorted(student_objects, key=lambda student: student.age)   # sort by age

Важность сортировки алгоритмов

Что такое сортировка? И почему это так важно? Это вопросы, которые мы постараемся ответить в этом разделе. Из книг в библиотеке и словах в словаре к записям базы данных и инструкции в процессоре мы испытали сортировку много раз

Из книг в библиотеке и словах в словаре к записям базы данных и инструкции в процессоре мы испытали сортировку много раз.

« в информатике, сортировка – это акт организации вещей в упорядоченной последовательности ». – Википедия

Это означает, что когда мы сортируем вещи, нам нужно знать критерии, на которые мы будем организовать последовательность, переданную нам. Для целей настоящего Учебника мы будем предполагать, что критерии – это значение числа, и мы сортируем заданную последовательность чисел.

В информатике наиболее важной целью сортировки состоит в том, чтобы произвести эффективные алгоритмы. Двоичный поиск – исключительно быстрый алгоритм поиска, который не будет возможно в несортированной коллекции объектов

Почти все установленные операции работают очень быстро на сортировке данных.

Помимо эффективных алгоритмов, сортировка используется, когда очень требование программы сортируется что-то, как программа, которая работает с палубой карт. Следовательно, алгоритмы сортировки являются одним из самых фундаментальных концепций, который должен знать программист.

Operator Module Functions

The key-function patterns shown above are very common, so Python provides convenience functions to make accessor functions easier and faster. The has itemgetter, attrgetter, and starting in Python 2.6 a methodcaller function.

Using those functions, the above examples become simpler and faster.

>>> from operator import itemgetter, attrgetter, methodcaller

>>> sorted(student_tuples, key=itemgetter(2))


>>> sorted(student_objects, key=attrgetter('age'))

The operator module functions allow multiple levels of sorting. For example, to sort by grade then by age:

>>> sorted(student_tuples, key=itemgetter(1,2))


>>> sorted(student_objects, key=attrgetter('grade', 'age'))

The third function from the operator module, methodcaller is used in the following example in which the weighted grade of each student is shown before sorting on it:

>>> 

>>> sorted(student_objects, key=methodcaller('weighted_grade'))

Python sort list of grades

There are various grading systems around the world. Our example contains
grades such as A+ or C- and these cannot be ordered lexicographically. We use
a dictionary where each grade has its given value.

grades.py

#!/usr/bin/env python3


data = 'A+ A A- B+ B B- C+ C C- D+ D'
grades = { grade: idx for idx, grade in enumerate(data.split()) } 

def mc(e):
    return grades.get(e)

students = 

print(grades)

students.sort(key=mc)
print(students)


# from operator import itemgetter
# students.sort(key=lambda e: itemgetter(e)(grades))

We have a list of students. Each student has a name and a grade in a nested
tuple.

data = 'A+ A A- B+ B B- C+ C C- D+ D'
grades = { grade: idx for idx, grade in enumerate(data.split()) } 

We build the dictionary of grades. Each grade has its value. The grades will
be sorted by their dictionary value.

def mc(e):
    return grades.get(e)

The key function simply returns the value of the grade.

# from operator import itemgetter
# students.sort(key=lambda e: itemgetter(e)(grades))

This solution uses an anonymous function.

$ ./grades.py 
{'A+': 0, 'A': 1, 'A-': 2, 'B+': 3, 'B': 4, 'B-': 5, 'C+': 6, 'C': 7, 'C-': 8, 'D+': 9, 'D': 10}

This is the output.

Реализация сортировки вставки

Реализация алгоритма сортировки вставки в языке программирования Python.

Выход:

Объяснение:

В приведенном выше коде python у нас есть список, содержащий 10 несортированных чисел для сортировки. В первом цикле while мы выполняем итерацию от 2-го элемента так, чтобы первый элемент списка стал первым элементом отсортированного списка. Первый цикл while выбирает элемент из несортированного списка, а второй цикл while (вложенный в первый) сравнивает его с элементами отсортированного списка, если выбранный элемент меньше соседнего левого элемента (отсортированной части), то левый элемент сдвигается на место текущего элемента и текущий элемент копируется на место левого элемента. Последний цикл while, наконец, отображает отсортированный список.

Анализ Сложности

Из псевдокода и приведенной выше иллюстрации следует, что сортировка вставки является эффективным алгоритмом по сравнению с пузырьковой сортировкой или сортировкой выбора. Вместо использования цикла for и текущих условий он использует цикл while, который больше не выполняет никаких дополнительных шагов при сортировке списка.

Однако, даже если мы передадим сортированный список методу сортировки вставки, он все равно выполнит внешний цикл for, тем самым требуя n шагов для сортировки уже отсортированного списка. Это делает наилучшую временную сложность сортировки вставки линейной функцией N, где N-количество элементов в списке .

Таким образом, различные сложности для метода сортировки вставки приведены ниже:

Таким образом, различные сложности для метода сортировки вставки приведены ниже:	O(n2)
В лучшем случае временная сложность	O(n)
Средняя временная сложность	O(n2)
Сложность пространства	O(1)

Несмотря на эти сложности, мы все еще можем сделать вывод, что сортировка вставки является наиболее эффективным алгоритмом по сравнению с другими методами сортировки, такими как Пузырьковая сортировка и сортировка выбора.

Пример 3: Отсортировать список с помощью ключа

# take second element for sort
def takeSecond(elem):
    return elem

# random list
random = 

# sort list with key
random.sort(key=takeSecond)

# print list
print('Sorted list:', random)

Выход

Sorted list: 

Возьмем другой пример. Предположим, у нас есть список информации о сотрудниках офиса, каждый элемент которого представляет собой словарь.

Мы можем отсортировать список следующим образом:

# sorting using custom key
employees = 

# custom functions to get employee info
def get_name(employee):
    return employee.get('Name')


def get_age(employee):
    return employee.get('age')


def get_salary(employee):
    return employee.get('salary')


# sort by name (Ascending order)
employees.sort(key=get_name)
print(employees, end='\n\n')

# sort by Age (Ascending order)
employees.sort(key=get_age)
print(employees, end='\n\n')

# sort by salary (Descending order)
employees.sort(key=get_salary, reverse=True)
print(employees, end='\n\n')

Выход

Здесь для первого случая наша настраиваемая функция возвращает имя каждого сотрудника. Поскольку имя представляет собой строку, Python по умолчанию сортирует его в алфавитном порядке.

Во втором случае возвращается возраст (int), который сортируется в порядке возрастания.

В третьем случае функция возвращает зарплату (int) и сортируется в порядке убывания с помощью reverse = True.

Рекомендуется использовать лямбда-функцию, когда функция может быть представлена в одной строке. Итак, мы также можем написать указанную выше программу как:

# sorting using custom key
employees = 

# sort by name (Ascending order)
employees.sort(key=lambda x: x.get('Name'))
print(employees, end='\n\n')

# sort by Age (Ascending order)
employees.sort(key=lambda x: x.get('age'))
print(employees, end='\n\n')

# sort by salary (Descending order)
employees.sort(key=lambda x: x.get('salary'), reverse=True)
print(employees, end='\n\n')

Выход

Было полезно224
Нет28

344cookie-checklist sort() в Python

Sorting

In computer science, sorting is arranging elements in an ordered sequence. Over the years,
several algorithms were developed to perform sorting on data, including merge sort,
quick sort, selection sort, or bubble sort. (The other meaning of sorting is categorizing;
it is grouping elements with similar properties.)

The opposite of sorting, rearranging a sequence of elements in a random or meaningless order,
is called shuffling.

Data can be sorted alphabetically or numerically. The sort key specifies
the criteria used to perform the sort. It is possible to sort objects by multiple keys.
For instance, when sorting users, the names of the users could be used as primary sort key,
and their occupation as the secondary sort key.

Пример сортировки пузыря

Учитывая последовательность: 12, 16, 11, 10, 14, 13 Количество элементов ( n ): 6 Давайте начнем-

Шаг 1: Переменные Я и J Представление отсортированных элементов и позиции.
Шаг 2: N 6. N.

Шаг 3: Установить Я Как 0. я

Шаг 4: Установить J Как 1. j

Шаг 5: Сравнение позиций J и J + 1 Элемент в положении 1 (12) не превышает один при 2 (16).
Шаг 6: Увеличение J Отказ j

Шаг 7: J (2) не N-I (6), поэтому мы идем к шагу 5.
Шаг 5: Положение 2 (16) больше, чем позиция 3 (11), поэтому мы поменяем.
Последовательность: 12, 11 , 16 , 10, 14, 13

Шаг 6: Увеличение J Отказ j

Шаг 7: 3 не 6, поэтому мы идем к шагу 5.
Шаг 5: 16 больше 10, поэтому мы поменяем. Последовательность: 12, 11, 10 , 16 , 14, 13

Шаг 6: Увеличение J Отказ j

Шаг 7: 4 не 6, поэтому мы идем к шагу 5.
Шаг 5: 16 больше 14, поэтому мы поменяем. Последовательность: 12, 11, 10, 14 , 16 13.

Шаг 6: Увеличение J Отказ j

Шаг 7: 5 не 6, поэтому мы идем к шагу 5.
Шаг 5: 16 больше 13, поэтому мы поменяем. Последовательность: 12, 11, 10, 14, 13 , 16.

Шаг 6: Увеличение J Отказ j

Шаг 7: J (6) равен N-I (6), поэтому мы переходим к шагу 8

Обратите внимание, что наибольший элемент (16) находится в конце, и мы отсортировали один элемент наверняка. Шаг 8: Увеличение я

я

Шаг 9: Я (1) не N-1 (5), поэтому мы повторяем все это по сравнению с шагом 4, а цикл продолжается, полученные изменения в последовательности будут выглядеть так:

11 , 12 , 10, 14, 13, 16 11, 10 , 12 , 14, 13, 16 11, 10, 12 , 14 , 13, 16 11, 10, 12, 13 , 14 , 16 10 , 11 12, 13, 14 , 16 10, 11 , 12 , 13, 14 , 16 10, 11, 12 , 13 , 14 , 16 10 , 11 12, 13 , 14 , 16 10, 11 , 12 , 13 , 14 , 16 10 , 11 , 12 , 13 , 14 , 16 10 , 11 , 12 , 13 , 14 , 16.

После этого Я становится 5, что это N-1 Таким образом, контурные контуры и алгоритм говорит нам, что список отсортирован. Также кажется, что список может быть отсортирован до окончания алгоритма, что просто означает, что заданная последовательность была несколько отсортирована до того, как она была передана алгоритму.

Stable sort

A stable sort is one where the initial order of equal elements is preserved.
Some sorting algorithms are naturally stable, some are unstable. For instance, the
merge sort and the bubble sort are stable sorting algorithms. On the other hand, heap
sort and quick sort are examples of unstable sorting algorithms.

Consider the following values: . A stable sorting
produces the following: . The ordering of the values
3 and 5 is kept. An unstable sorting may produce the following: .

Python uses the timsort algorithm. It is a hybrid stable sorting algorithm,
derived from merge sort and insertion sort. It was implemented by Tim Peters
in 2002 for use in the Python programming language.

Python sort list by case

By default, the strings with uppercase first letters are sorted before
the other strings. We can sort strings regardless of their case as well.

case_sorting.py

#!/usr/bin/env python3


text = 'Today is a beautiful day. Andy went fishing.'
words = text.replace('.', '')

sorted_words = sorted(words.split(), key=str.lower)
print('Case insensitive:', sorted_words)

sorted_words2 = sorted(words.split())
print('Case sensitive:', sorted_words2)

By providing the function to the key
attribute, we perform a case insensitive sorting.

$ ./case_sorting.py 
Case insensitive: 
Case sensitive: 

This is the output.

Входные данные не меняются

Пусть есть два списка и .

Начнем с самого простого алгоритма: обозначим метки за и и будем брать меньший из , и увеличивать его метку на единицу, пока одна из меток не выйдет за границу списка.

При первом сравнении мы выберем минимальный элемент из двух минимальных в своем списке и подвинемся на следующий элемент, поэтому наименьший элемент из двух списков будет стоять на нулевом месте результирующего. Дальше несложно по индукции доказать, что далее слияние пройдет верно.

Перейдем к коду:

Заметим, что в данном коде используется только перемещение вперед по списку. Поэтому будет достаточно работать с итераторами. Перепишем алгоритм с помощью итераторов.

Еще изменим обработку концов списков, так как теперь мы не умеем копировать сразу до конца. Будем обрабатывать элементы до того, когда оба итератора дойдут до конца, при этом, если один уже оказался в конце, будем просто брать из второго.

В этой реализации можно вместо добавления по одному элементу () собрать генератор, а потом из него получить список. Для этого напишем отдельную функцию, которая будет строить генератор, а основная функция сделает из него список.

Встроенные реализации

Рассмотрим еще несколько способов слияния через встроенные в python функции.

• из . Как говорит документация, эта функция делает именно то, что мы хотим, и больше: объединяет несколько итерируемых объекта, можно задать ключ, можно сортировать в обратном порядке.

  Тогда нам нужно просто импортировать и использовать:

• из . умеет считать количество вхождений каждого из элементов, выдавать их в тех количествах, в которых они входят, и еще несколько полезных вещей, которые сейчас не нужны (например, несколько самых часто встречающихся элементов).

  Воспользуемся для слияния элементов и :

• И, наконец, просто сортировка. Объединяем и сортируем заново.