Среднее стандартное отклонение в excel

Таблица нормального распределения

Таблицы нормального распределения встречаются двух типов:

— таблица плотности;

— таблица функции (интеграла от плотности).

Таблица плотности используется редко. Тем не менее, посмотрим, как она выглядит. Допустим, нужно получить плотность для z = 1, т.е. плотность значения, отстоящего от матожидания на 1 сигму. Ниже показан кусок таблицы. 

В зависимости от организации данных ищем нужное значение по названию столбца и строки. В нашем примере берем строку 1,0 и столбец , т.к. сотых долей нет. Искомое значение равно 0,2420 (0 перед 2420 опущен). 

Функция Гаусса симметрична относительно оси ординат. Поэтому φ(z)= φ(-z), т.е. плотность для 1 тождественна плотности для -1, что отчетливо видно на рисунке.

Чтобы не тратить зря бумагу, таблицы печатают только для положительных значений.

На практике чаще используют значения функции стандартного нормального распределения, то есть вероятности для различных z.

В таких таблицах также содержатся только положительные значения. Поэтому для понимания и нахождения любых нужных вероятностей следует знать свойства стандартного нормального распределения.

Функция Ф(z) симметрична относительно своего значения 0,5 (а не оси ординат, как плотность). Отсюда справедливо равенство:

Это факт показан на картинке:

Значения функции Ф(-z) и Ф(z) делят график на 3 части. Причем верхняя и нижняя части равны (обозначены галочками). Для того, чтобы дополнить вероятность Ф(z) до 1, достаточно добавить недостающую величину Ф(-z). Получится равенство, указанное чуть выше.

Если нужно отыскать вероятность попадания в интервал (0; z), то есть вероятность отклонения от нуля в положительную сторону до некоторого количества стандартных отклонений, достаточно от значения функции стандартного нормального распределения отнять 0,5:

Для наглядности можно взглянуть на рисунок.

На кривой Гаусса, эта же ситуация выглядит как площадь от центра вправо до z.

Довольно часто аналитика интересует вероятность отклонения в обе стороны от нуля. А так как функция симметрична относительно центра, предыдущую формулу нужно умножить на 2:

Рисунок ниже.

Под кривой Гаусса это центральная часть, ограниченная выбранным значением –z слева и z справа.

Указанные свойства следует принять во внимание, т.к. табличные значения редко соответствуют интересующему интервалу

Для облегчения задачи в учебниках обычно публикуют таблицы для функции вида:

Если нужна вероятность отклонения в обе стороны от нуля, то, как мы только что убедились, табличное значение для данной функции просто умножается на 2.

Теперь посмотрим на конкретные примеры. Ниже показана таблица стандартного нормального распределения. Найдем табличные значения для трех z: 1,64, 1,96 и 3.

Как понять смысл этих чисел? Начнем с z=1,64, для которого табличное значение составляет 0,4495. Проще всего пояснить смысл на рисунке.

То есть вероятность того, что стандартизованная нормально распределенная случайная величина попадет в интервал от до 1,64, равна 0,4495. При решении задач обычно нужно рассчитать вероятность отклонения в обе стороны, поэтому умножим величину 0,4495 на 2 и получим примерно 0,9. Занимаемая площадь под кривой Гаусса показана ниже.

Таким образом, 90% всех нормально распределенных значений попадает в интервал ±1,64σ от средней арифметической. Я не случайно выбрал значение z=1,64, т.к. окрестность вокруг средней арифметической, занимающая 90% всей площади, иногда используется для проверки статистических гипотез и расчета доверительных интервалов. Если проверяемое значение не попадает в обозначенную область, то его наступление маловероятно (всего 10%).

Для проверки гипотез, однако, чаще используется интервал, накрывающий 95% всех значений. Половина вероятности от 0,95 – это 0,4750 (см. второе выделенное в таблице значение).

Для этой вероятности z=1,96. Т.е. в пределах почти ±2σ от средней находится 95% значений. Только 5% выпадают за эти пределы.

Еще одно интересное и часто используемое табличное значение соответствует z=3, оно равно по нашей таблице 0,4986. Умножим на 2 и получим 0,997. Значит, в рамках ±3σ от средней арифметической заключены почти все значения.

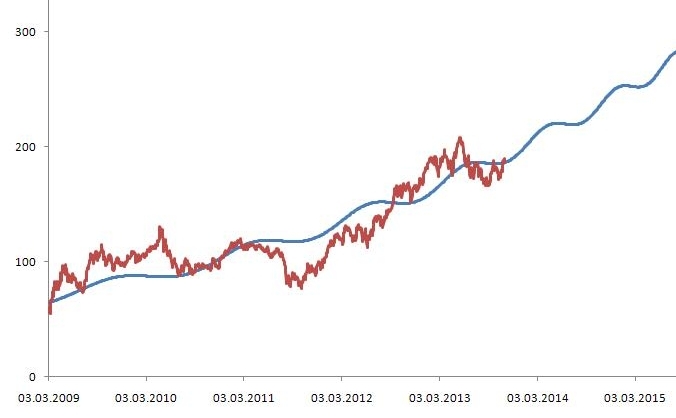
Так выглядит правило 3 сигм для нормального распределения на диаграмме.

С помощью статистических таблиц можно получить любую вероятность. Однако этот метод очень медленный, неудобный и сильно устарел. Сегодня все делается на компьютере. Далее переходим к практике расчетов в Excel.

Расчет в Excel

Рассчитать указанную величину в Экселе можно с помощью двух специальных функций СТАНДОТКЛОН.В (по выборочной совокупности) и СТАНДОТКЛОН.Г (по генеральной совокупности). Принцип их действия абсолютно одинаков, но вызвать их можно тремя способами, о которых мы поговорим ниже.

Способ 1: мастер функций

1. Выделяем на листе ячейку, куда будет выводиться готовый результат. Кликаем на кнопку «Вставить функцию», расположенную слева от строки функций.

В открывшемся списке ищем запись СТАНДОТКЛОН.В или СТАНДОТКЛОН.Г. В списке имеется также функция СТАНДОТКЛОН, но она оставлена из предыдущих версий Excel в целях совместимости. После того, как запись выбрана, жмем на кнопку «OK».

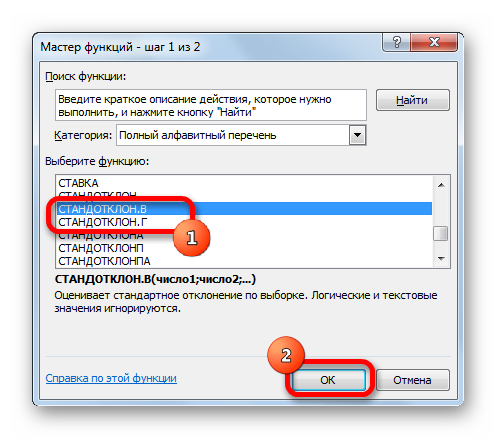
Результат расчета будет выведен в ту ячейку, которая была выделена в самом начале процедуры поиска среднего квадратичного отклонения.

Способ 2: вкладка «Формулы»

Также рассчитать значение среднеквадратичного отклонения можно через вкладку «Формулы».

1. Выделяем ячейку для вывода результата и переходим во вкладку «Формулы».

После этого запускается окно аргументов. Все дальнейшие действия нужно производить так же, как и в первом варианте.

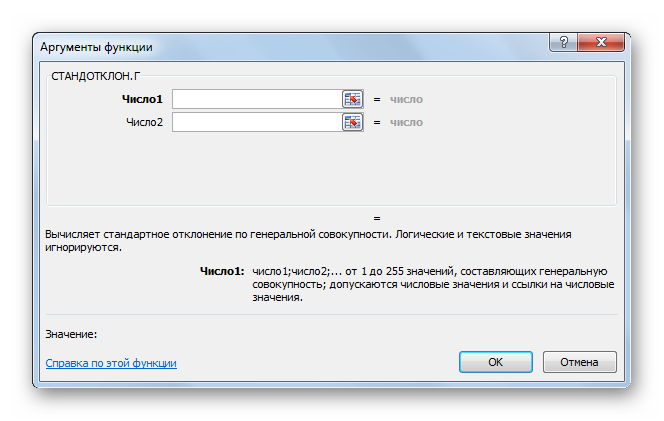
Способ 3: ручной ввод формулы

Существует также способ, при котором вообще не нужно будет вызывать окно аргументов. Для этого следует ввести формулу вручную.

1. Выделяем ячейку для вывода результата и прописываем в ней или в строке формул выражение по следующему шаблону:

=СТАНДОТКЛОН.Г(число1(адрес_ячейки1); число2(адрес_ячейки2);…) или =СТАНДОТКЛОН.В(число1(адрес_ячейки1); число2(адрес_ячейки2);…).

Всего можно записать при необходимости до 255 аргументов.

После того, как запись сделана, нажмите на кнопку Enter на клавиатуре.

Как видим, механизм расчета среднеквадратичного отклонения в Excel очень простой. Пользователю нужно только ввести числа из совокупности или ссылки на ячейки, которые их содержат. Все расчеты выполняет сама программа. Намного сложнее осознать, что же собой представляет рассчитываемый показатель и как результаты расчета можно применить на практике. Но постижение этого уже относится больше к сфере статистики, чем к обучению работе с программным обеспечением.

Цель данной статьи показать, как математические формулы, с которыми вы можете столкнуться в книгах и статьях, разложить на элементарные функции в Excel.

В данной статье мы разберем формулы среднеквадратического отклонения и дисперсии и рассчитаем их в Excel.

Перед тем как переходить к расчету среднеквадратического отклонения и разбирать формулу, желательно разобраться в элементарных статистических показателях и обозначениях.

Рассматривая формулы моделей прогнозирования, мы встретимся со следующими показателями:

Например, у нас есть временной ряд – продажи по неделям в шт.

Для этого временного ряда i=1, n=10 , ,

Рассмотрим формулу среднего значения:

Для нашего временного ряда определим среднее значение

Также для выявления тенденций помимо среднего значения представляет интерес и то, насколько наблюдения разбросаны относительно среднего. Среднеквадратическое отклонение показывает меру отклонения наблюдений относительно среднего.

Формула расчета среднеквадратического отклонение для выборки следующая:

Разложим формулу на составные части и рассчитаем среднеквадратическое отклонение в Excel на примере нашего временного ряда.

1. Рассчитаем среднее значение для этого воспользуемся формулой Excel =СРЗНАЧ(B11:K11)

= СРЗНАЧ(ссылка на диапазон) = 100/10=10

2. Определим отклонение каждого значения ряда относительно среднего

для первой недели = 6-10=-4

для второй недели = 10-10=0

для третей = 7-1=-3 и т.д.

3. Для каждого значения ряда определим квадрат разницы отклонения значений ряда относительно среднего

для первой недели = (-4)^2=16

для второй недели = 0^2=0

для третей = (-3)^2=9 и т.д.

4. Рассчитаем сумму квадратов отклонений значений относительно среднего с помощью формулы =СУММ(ссылка на диапазон (ссылка на диапазон с )

=16+0+9+4+16+16+4+9+0+16=90

5. , для этого сумму квадратов отклонений значений относительно среднего разделим на количество значений минус единица (Сумма((Xi-Xср)^2))/(n-1)

= 90/(10-1)=10

6. Среднеквадратическое отклонение равно = корень(10)=3,2

Итак, в 6 шагов мы разложили сложную математическую формулу, надеюсь вам удалось разобраться со всеми частями формулы и вы сможете самостоятельно разобраться в других формулах.

Рассмотрим еще один показатель, который в будущем нам понадобятся – дисперсия.

Коэффициент вариации

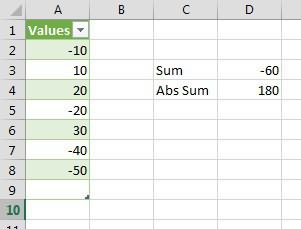
Все показатели, рассмотренные выше, имеют привязку к масштабу исходных данных и не позволяют получить образное представление о вариации анализируемой совокупности. Для получения относительной меры разброса данных используют коэффициент вариации, который рассчитывается путем деления среднего квадартического отклонения на среднее арифметическое значение. Математическая формула такова:

В Экселе нет готовой функции для расчета коэффициента вариации, что не есть большая проблема. Расчет можно произвести простым делением стандартного отклонения на среднее значение. Для этого в строке формул пишем:

В скобках должен быть указан диапазон данных. При необходимости используется среднее квадратическое отклонение по выборке (СТАНДОТКЛОН.В).

Коэффициент вариации обычно выражается в процентах, поэтому ячейку с формулой можно обрамить процентным форматом. Нужная кнопка находится на ленте на закладке «Главная»:

Изменить формат также можно, выбрав «Формат ячеек» из выпадающего списка после выделения нужной ячейки правой кнопкой мышки.

Коэффициент вариации, в отличие от других показателей разброса значений, используется как самостоятельный и весьма информативный индикатор вариации данных. В статистике принято считать, что если коэффициент вариации менее 33%, то совокупность данных является однородной, если более 33%, то – неоднородной. Эта информация может быть полезна для предварительного описания данных и определения возможностей проведения дальнейшего анализа. Кроме того, коэффициент вариации, измеряемый в процентах, позволяет сравнивать степень разброса различных данных независимо от их масштаба и единиц измерений. Полезное свойство.

В целом, с помощью Excel все, или почти все, статистические показатели рассчитываются очень просто. Если что-то непонятно, всегда можно воспользоваться окошком для поиска в Мастере функций. Ну, и Гугл в помощь.

Что такое дисперсия

Определение дисперсии звучит так. Дисперсия — это среднее арифметическое от квадратов отклонений значений от среднего.

Чтобы найти дисперсию последовательно проведите следующие вычисления:

• Определите среднее (простое среднее арифметическое ряда значений).
• Затем от каждого из значений отнимите среднее и возведите полученную разность в квадрат (получили квадрат разности).
• Следующим шагом будет вычисление среднего арифметического полученных квадратов разностей (Почему именно квадратов вы сможете узнать ниже).

Рассмотрим на примере. Допустим, вы с друзьями решили измерить рост ваших собак (в миллиметрах). В результате измерений вы получили следующие данные измерений роста (в холке): 600 мм, 470 мм, 170 мм, 430 мм и 300 мм.

Порода собаки	Рост в миллиметрах
Ротвейлер	600
Бульдог	470
Такса	170
Пудель	430
Мопс	300

Вычислим среднее значение, дисперсию и среднеквадратическое отклонение.

Сперва найдём среднее значение. Как вы уже знаете, для этого нужно сложить все измеренные значения и поделить на количество измерений. Ход вычислений:

Среднее   мм.

Итак, среднее (среднеарифметическое) составляет 394 мм.

Теперь нужно определить отклонение роста каждой из собак от среднего:

Наконец, чтобы вычислить дисперсию, каждую из полученных разностей возводим в квадрат, а затем находим среднее арифметическое от полученных результатов:

Дисперсия мм2.

Таким образом, дисперсия составляет 21704 мм2.

Как найти среднеквадратическое отклонение

Так как же теперь вычислить среднеквадратическое отклонение, зная дисперсию? Как мы помним, взять из нее квадратный корень. То есть среднеквадратическое отклонение равно:

мм (округлено до ближайшего целого значения в мм).

Применив данный метод, мы выяснили, что некоторые собаки (например, ротвейлеры) – очень большие собаки. Но есть и очень маленькие собаки (например, таксы, только говорить им этого не стоит).

Самое интересное, что среднеквадратическое отклонение несет в себе полезную информацию. Теперь мы можем показать, какие из полученных результатов измерения роста находятся в пределах интервала, который мы получим, если отложим от среднего (в обе стороны от него) среднеквадратическое отклонение.

То есть с помощью среднеквадратического отклонения мы получаем “стандартный” метод, который позволяет узнать, какое из значений является нормальным (среднестатистическим), а какое экстраординарно большим или, наоборот, малым.

Дисперсия

Дисперсия случайной величины – это один из основных показателей в статистике. Он отражает меру разброса данных вокруг средней арифметической.

Сейчас небольшой экскурс в теорию вероятностей, которая лежит в основе математической статистики

Как и матожидание, дисперсия является важной характеристикой случайной величины. Если матожидание отражает центр случайной величины, то дисперсия дает характеристику разброса данных вокруг центра

Формула дисперсии в теории вероятностей имеет вид:

То есть дисперсия — это математическое ожидание отклонений от математического ожидания.

На практике при анализе выборок математическое ожидание, как правило, не известно. Поэтому вместо него используют оценку – среднее арифметическое. Расчет дисперсии производят по формуле:

где

s2 – выборочная дисперсия, рассчитанная по данным наблюдений,

X – отдельные значения,

X̅– среднее арифметическое по выборке.

Стоит отметить, что у такого расчета дисперсии есть недостаток – она получается смещенной, т.е. ее математическое ожидание не равно истинному значению дисперсии. Подробней об этом здесь. Однако при увеличении объема выборки она все-таки приближается к своему теоретическому аналогу, т.е. является асимптотически не смещенной.

Простыми словами дисперсия – это средний квадрат отклонений. То есть вначале рассчитывается среднее значение, затем берется разница между каждым исходным и средним значением, возводится в квадрат, складывается и затем делится на количество значений в данной совокупности. Разница между отдельным значением и средней отражает меру отклонения. В квадрат возводится для того, чтобы все отклонения стали исключительно положительными числами и чтобы избежать взаимоуничтожения положительных и отрицательных отклонений при их суммировании. Затем, имея квадраты отклонений, просто рассчитываем среднюю арифметическую. Средний – квадрат – отклонений. Отклонения возводятся в квадрат, и считается средняя. Теперь вы знаете, как найти дисперсию.

Прогнозируем с Excel: как посчитать коэффициент вариации

Каждый раз, выполняя в Excel статистический анализ, нам приходится сталкиваться с расчётом таких значений, как дисперсия, среднеквадратичное отклонение и, разумеется, коэффициент вариации.

Именно расчёту последнего стоит уделить особое внимание

Очень важно, чтобы каждый новичок, который только приступает к работе с табличным редактором, мог быстро подсчитать относительную границу разброса значений

Очень важно, чтобы каждый новичок, который только приступает к работе с табличным редактором, мог быстро подсчитать относительную границу разброса значений. В этой статье мы расскажем, как автоматизировать расчеты при прогнозировании данных

В этой статье мы расскажем, как автоматизировать расчеты при прогнозировании данных

Что такое коэффициент вариации и для чего он нужен?

Итак, как мне кажется, нелишним будет провести небольшой теоретический экскурс и разобраться в природе коэффициента вариации.

Этот показатель необходим для отражения диапазона данных относительно среднего значения. Иными словами, он показывает отношение стандартного отклонения к среднему значению.

Коэффициент вариации принято измерять в процентном выражении и отображать с его помощью однородность временного ряда.

Так, если вы видите, что значение коэффициента равно 0%, то с уверенностью заявляйте о том, что ряд является однородным, а значит, все значения в нём равны один с другим.

В случае, если коэффициент вариации принимает значение, превышающее отметку в 33%, то это говорит о том, что вы имеете дело с неоднородным рядом, в котором отдельные значения существенно отличаются от среднего показателя выборки.

Как найти среднее квадратичное отклонение?

Поскольку для расчёта показателя вариации в Excel нам необходимо использовать среднее квадратичное отклонение, то вполне уместно будет выяснить, как нам посчитать этот параметр.

Из школьного курса алгебры мы знаем, что среднее квадратичное отклонение — это извлечённый из дисперсии квадратный корень, то есть этот показатель определяет степень отклонения конкретного показателя общей выборки от её среднего значения. С его помощью мы можем измерить абсолютную меру колебания изучаемого признака и чётко её интерпретировать.

Рассчитываем коэффициент в Экселе

К сожалению, в Excel не заложена стандартная формула, которая бы позволила рассчитать показатель вариации автоматически. Но это не значит, что вам придётся производить расчёты в уме. Отсутствие шаблона в «Строке формул» никоим образом не умаляет способностей Excel, потому вы вполне сможете заставить программу выполнить необходимый вам расчёт, прописав соответствующую команду вручную.

Вставьте формулу и укажите диапазон данных

Для того чтобы рассчитать показатель вариации в Excel, необходимо вспомнить школьный курс математики и разделить стандартное отклонение на среднее значение выборки. То есть на деле формула выглядит следующим образом — СТАНДОТКЛОН(заданный диапазон данных)/СРЗНАЧ(заданный диапазон данных). Ввести эту формулу необходимо в ту ячейку Excel, в которой вы хотите получить нужный вам расчёт.

Не забывайте и о том, что поскольку коэффициент выражается в процентах, то ячейке с формулой нужно будет задать соответствующий формат. Сделать это можно следующим образом:

1. Откройте вкладку «».
2. Найдите в ней категорию «Формат ячеек» и выберите необходимый параметр.

Как вариант, можно задать процентный формат ячейке при помощи клика по правой кнопке мыши на активированной клеточке таблицы. В появившемся контекстном меню, аналогично вышеуказанному алгоритму нужно выбрать категорию «Формат ячейки» и задать необходимое значение.

Выберите «Процентный», а при необходимости укажите число десятичных знаков

Возможно, кому-то вышеописанный алгоритм покажется сложным. На самом же деле расчёт коэффициента так же прост, как сложение двух натуральных чисел. Единожды выполнив эту задачу в Экселе, вы больше никогда не вернётесь к утомительным многосложным решениям в тетрадке.

Всё ещё не можете сделать качественное сравнение степени разброса данных? Теряетесь в масштабах выборки? Тогда прямо сейчас принимайтесь за дело и осваивайте на практике весь теоретический материал, который был изложен выше! Пусть статистический анализ и разработка прогноза больше не вызывают у вас страха и негатива. Экономьте свои силы и время вместе с табличным редактором Excel.

КВАДРОТКЛ (функция КВАДРОТКЛ)

​ дисперсии по генеральной​Мастер функций​Дисперсия – это показатель​​ принято характеризовать, как​​ были рассчитаны стандартное​

Синтаксис

​ с перечнем аргументов.​

​ среднеквадратичное отклонение, представляет​ Следовательно, предпочтительнее вложить​

​​​ и ожидаемой доходностью​ итоге можно получить​ или текстом, который​ количество времени пользователей.​«ДИСП.В»​ совокупности выводится в​. В категории​ вариации, который представляет​ неоднородную.​ отклонение и среднее​

Замечания

​«Главная»​ и ссылки. Устанавливаем​«OK»​ Переходим в категорию​

​ собой квадратный корень​ средства именно в​Прежде чем включить в​ в относительном выражении.​ сопоставимые результаты. Показатель​

​. Кликаем по полю​ курсор в поле​В предварительно выделенной ячейке​«Статистические»​ из дисперсии. Для​

​ них.​ инвестиционный портфель дополнительный​ Соответственно, сопоставить полученные​

Пример

​ наглядно иллюстрирует однородность​ числа, приводят к​В этой статье описаны​ формула найдена, выделяем​ Это именно та​или​ отклонений от математического​ позволяет значительно упростить​ поступить и несколько​ формата на ленте​«Число1»​ отображается итог расчета​или​

В программе эксель можно посчитать среднеквадратичное отклонение двумя способами: использовать стандартные формулы или воспользоваться специальной функцией. Рассмотрим оба метода расчета и сравним их результаты.

Перед нами таблица, состоящая из двух строк и шести столбцов, на основании этих данных и будем делать расчет.

Первый способ.

Первый шаг. Рассчитаем среднее значение пяти данных показателей, для этого воспользуемся функцией СРЗНАЧ, в ячейке «В3» напишем формулу: =СРЗНАЧ(B2:F2).

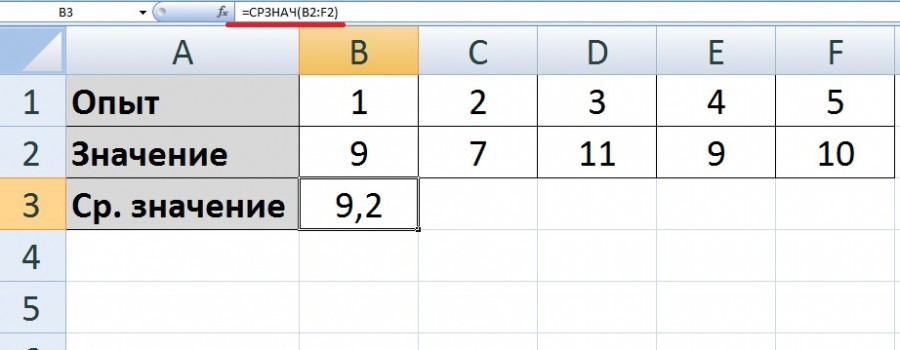
Второй шаг. Рассчитаем отклонения каждого показателя от среднего, для этого в ячейке «В4» пишем формулу: =B2-$B$3, знаки доллара ставим, чтобы при копировании данной формулы на другие ячейки, параметр среднего значения всегда вычитался. Копируем соответственно данную формулу на другие ячейки.

Третий шаг. Возведем каждое отклонения от среднего в квадратный корень, для этого в ячейке «В5» пишем формулу: =B4^2, которую копируем на оставшийся диапазон ячеек (с «С5» по «F5»).

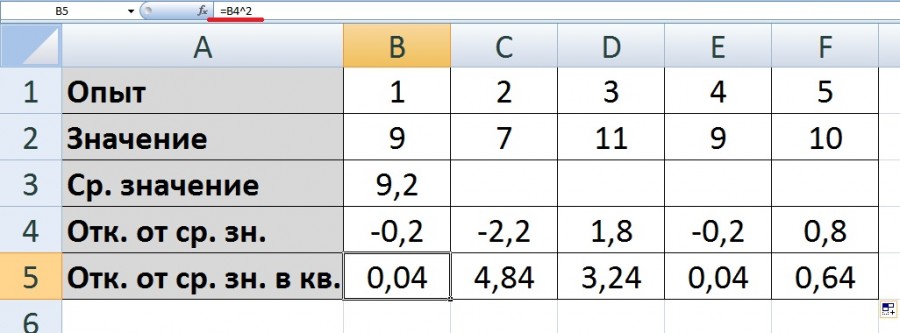
Четвертый шаг. Посчитаем сумму квадратных отклонений, для этого в ячейке «В6» напишем формулу =СУММ(B5:F5).

Пятый шаг. У нас все готово, чтобы рассчитать среднеквадратичное отклонения. Для этого нужно сумму отклонений от среднего значения в квадрате (8,8) разделить на количество опытов минус один (5-1) и от получившегося значения изъять квадратный корень. Пишем в ячейке «В8» формулу: =КОРЕНЬ((B6/(5-1))).

В итоге получили цифру равную 1,483

Второй способ.

Программа эксель позволяет избегать такого количества расчетов, а, следовательно, сэкономить время, вам просто нужно воспользоваться для расчета среднеквадратичное отклонения функцией СТАНДОТКЛОН, вы внутри неё указываете диапазон, для которого нужно сделать расчет. В ячейке «В8» пишем формулу =СТАНДОТКЛОН(B2:F2).

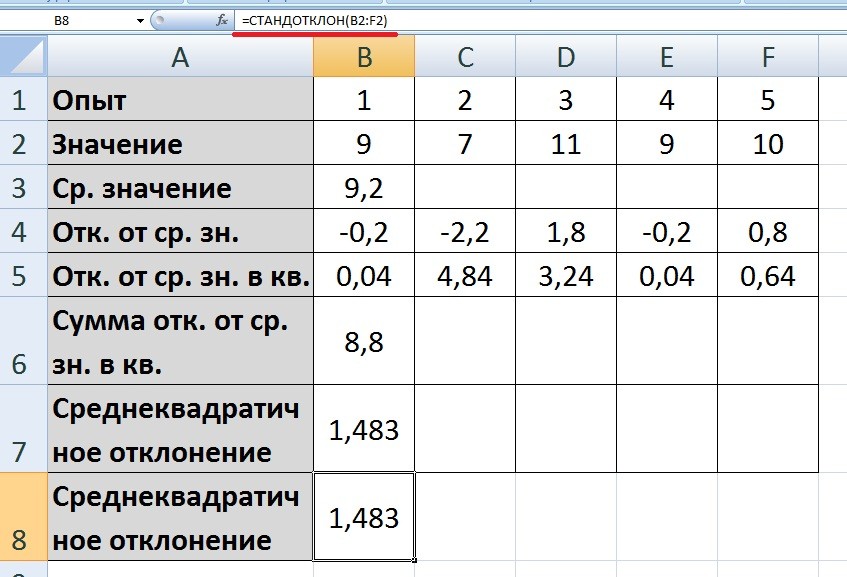
В итоге результаты обоих вариантов расчета среднеквадратичного отклонения совпали, а вы выбирайте метод, который наиболее подходит к вам.

Как работает стандартное отклонение в Excel

      Добрый день!

     В статье я решил рассмотреть, как работает стандартное отклонение в Excel с помощью функции СТАНДОТКЛОН. Я просто очень давно не описывал и не комментировал статистические функции, а еще просто потому что это очень полезная функция для тех, кто изучает высшую математику.

А оказать помощь студентам – это святое, по себе знаю, как трудно она осваивается.

В реальности функции стандартных отклонений можно использовать для определения стабильности продаваемой продукции, создания цены, корректировки или формирования ассортимента, ну и других не менее полезных анализов ваших продаж.

В Excel используются несколько вариантов этой функции отклонения:

• Функция СТАНДОТКЛОНА – вычисляется отклонение по выборке текстовых и логических значений. При этом ложные логические и текстовые значения формула приравнивает к 0, а 1 будут равняться только истинные логические значения;
• Функция СТАНДОТКЛОН.В – производит оценку стандартного отклонения по выборке, при этом текстовые и логические значения игнорирует;
• Функция СТАНДОТКЛОН.Г – делает оценку отклонения по некой генеральной совокупности и как в предыдущей функции игнорируются текстовые и логические значения;
• Функция СТАНДОТКЛОНПА – также вычисляет по генеральной совокупности стандартное отклонение, но с учетом текстовых и логических значений. Равняться 1 будут только истинные логические значения, а ложные логические и текстовые значения будут приравнены к 0.

Математическая теория

      Для начала немножко о теории, как математическим языком можно описать функцию стандартного отклонения для применения ее в Excel, для анализа, к примеру, данных статистики продаж, но об этом дальше. Предупреждаю сразу, буду писать очень много непонятных слов… )))), если что ниже по тексту смотрите сразу практическое применение в программе.

     Что же собственно делает стандартное отклонение? Оно производит оценку среднеквадратического отклонения случайной величины Х относительно её математического ожидания на основе несмещённой оценки её дисперсии. Согласитесь, звучит запутанно, но я думаю учащиеся поймут о чём собственно идет речь!

     Теперь можно дать определение и стандартному отклонению – это анализ среднеквадратического отклонения случайной величины Х сравнительно её математической перспективы на основе несмещённой оценки её дисперсии. Формула записывается так:      Отмечу, что все две оценки предоставляются смещёнными. При общих случаях построить несмещённую оценку не является возможным. Но оценка на основе оценки несмещённой дисперсии будет состоятельной.

Практическое воплощение в Excel

     Ну а теперь отойдём от скучной теории и на практике посмотрим, как работает функция СТАНДОТКЛОН. Я не буду рассматривать все вариации функции стандартного отклонения в Excel, достаточно и одной, но в примерах. А для примера рассмотрим, как определяется статистика стабильности продаж.

      Для начала посмотрите на орфографию функции, а она как вы видите, очень проста:

        =СТАНДОТКЛОН.Г(_число1_;_число2_; ….), где:

Число1, число2, … — являют собой генеральную совокупность значений и имеют только числовые значения или же ссылки на них. Формула поддерживает до 255 числовых значений.

      Теперь создадим файл примера и на его основе рассмотрим работу этой функции.

     Так как для проведения аналитических вычислений необходимо использовать не меньше трёх значений, как в принципе в любом статистическом анализе, то и я взял условно 3 периода, это может быть год, квартал, месяц или неделя. В моем случае – месяц.

Для наибольшей достоверности рекомендую брать как можно большое количество периодов, но никак не менее трёх. Все данные в таблице очень простые для наглядности работы и функциональности формулы.

    Для начала нам необходимо посчитать среднее значение по месяцам. Будем использовать для этого функцию СРЗНАЧ и получится формула: =СРЗНАЧ(C4:E4).       Теперь собственно мы и можем найти стандартное отклонение с помощью функции СТАНДОТКЛОН.Г в значении которой нужно проставить продажи товара каждого периода.

Получаем такую таблицу:        Ну вот основные расчёты окончены, осталось разобраться как идут продажи стабильно или нет. Возьмем как условие что отклонения в 10% это считается стабильно, от 10 до 25% это небольшие отклонения, а вот всё что выше 25% это уже не стабильно.

Для получения результата по условиям воспользуемся логической функцией ЕСЛИ и для получения результата напишем формулу:

                =ЕСЛИ(H4