Числа: целые, вещественные, комплексные
Содержание:
- Функция compare()
- Число Пи из библиотеки math
- Функция экспоненты exp() в Python
- Операторы присваивания Python
- Сравнение двойной косой черты python с другими языками программирования
- Оценка производительности
- 2 ответа
- Реализация KNN в Python
- Кубический корень
- Функция exp() — вычисление экспоненты
- Степень
- Связь с другими языками
- Встроенные структуры данных Python
- Транспонирование матрицы
- Выполнение операции сложения в векторе
- Математические операторы Python 3
- Стилизация print
- Многопоточность (многозадачность)
- Программа на Python с векторизацией и построением графиков
- Максимальные и минимальные
- Примеры решения задач
- Программа на Python с переменными
- 8 ответов
Функция compare()
Функция сравнивает два числа с десятичной запятой и возвращает значения в зависимости от условий следующим образом:
- Возвращает -1, если первое десятичное число меньше второго десятичного числа.
- Возвращает 1, если первое десятичное число больше второго десятичного числа.
- Возвращает 0, если оба значения десятичной точки равны.
Пример:
import decimal as d
valx = d.Decimal(122.20)
valy = d.Decimal(123.01)
print("Value 1: ",valx)
print("Value 2: ",valy)
compare = valx.compare(valy)
print(compare)
Выход:
Value 1: 122.2000000000000028421709430404007434844970703125 Value 2: 123.0100000000000051159076974727213382720947265625 -1
Число Пи из библиотеки math
Первой важной математической константой является число Пи (π). Оно обозначает отношение длины окружности к диаметру, его значение 3,141592653589793
Чтобы получить к нему доступ, сначала импортируем библиотеку math следующим образом:
Python
import math
| 1 | importmath |
Затем можно получить доступ к константе, вызывая :
Python
math.pi
| 1 | math.pi |
Вывод
Shell
3.141592653589793
| 1 | 3.141592653589793 |
Данную константу можно использовать для вычисления площади или длины окружности. Далее представлен пример простого кода, с помощью которого это можно сделать:
Python
import math
radius = 2
print(‘Площадь окружности с радиусом 2 равна:’, math.pi * (radius ** 2))
|
1 2 3 4 |
importmath radius=2 print(‘Площадь окружности с радиусом 2 равна:’,math.pi*(radius**2)) |
Вывод
Shell
Площадь окружности с радиусом 2 равна: 12.566370614359172
| 1 | Площадьокружностисрадиусом2равна12.566370614359172 |
Мы возвели радиус во вторую степень и умножили значение на число Пи, как и следовало сделать в соответствии с формулой πr2.
Функция экспоненты exp() в Python
Библиотека Math в Python поставляется с функцией , которую можно использовать для вычисления значения . К примеру, — экспонента от . Значение равно .
Метод может быть использован со следующим синтаксисом:
Python
math.exp(x)
| 1 | math.exp(x) |
Параметр может быть положительным или отрицательным числом. Если не число, метод возвращает ошибку. Рассмотрим пример использования данного метода:
Python
import math
# Инициализация значений
an_int = 6
a_neg_int = -8
a_float = 2.00
# Передача значений методу exp() и вывод
print(math.exp(an_int))
print(math.exp(a_neg_int))
print(math.exp(a_float))
|
1 2 3 4 5 6 7 8 9 10 11 |
importmath an_int=6 a_neg_int=-8 a_float=2.00 print(math.exp(an_int)) print(math.exp(a_neg_int)) print(math.exp(a_float)) |
Вывод
Shell
403.4287934927351
0.00033546262790251185
7.38905609893065
|
1 2 3 |
403.4287934927351 0.00033546262790251185 7.38905609893065 |
Мы объявили три переменные и присвоили им значения с различными числовыми типами данных. Мы передали значения методу для вычисления их экспоненты.
Мы также можем применить данный метод для встроенных констант, что продемонстрировано ниже:
Python
import math
print(math.exp(math.e))
print(math.exp(math.pi))
|
1 2 3 4 |
importmath print(math.exp(math.e)) print(math.exp(math.pi)) |
Вывод
Shell
15.154262241479262
23.140692632779267
|
1 2 |
15.154262241479262 23.140692632779267 |
При передаче не числового значения методу будет сгенерирована , как показано далее:
Python
import math
print(math.exp(«20»))
|
1 2 3 |
importmath print(math.exp(«20»)) |
Вывод
Shell
Traceback (most recent call last):
File «C:/Users/admin/mathe.py», line 3, in <module>
print (math.exp(«20»))
TypeError: a float is required
|
1 2 3 4 |
Traceback(most recent call last) File»C:/Users/admin/mathe.py»,line3,in<module> print(math.exp(«20»)) TypeErrorafloatisrequired |
Как видно из примера выше, генерируется ошибка .
Операторы присваивания Python
Оператор «=» присваивает значение, расположенное справа, переменной слева. Например, v = 23 присваивает значение числа 23 переменной v.
В программировании часто используют составные операторы присваивания. Они соединяют арифметический оператор с оператором «=». Поэтому для сложения мы используем оператор «+» с оператором «=», чтобы получить составной оператор «+=». Пример:
w = 5 w += 1 print(w)
Вывод
6
Сначала мы задаём переменной значение . Затем используем составной оператор присваивания , чтобы прибавить число справа, к переменной, расположенной слева, и присвоить результат переменной .
Составные операторы присваивания часто используются в циклах for:
for x in range (0, 7):
x *= 2
print(x)
Вывод
0 2 4 6 8 10 12
При помощи for можно автоматизировать процесс использования оператора «. Он умножает переменную на число , а затем присваивает полученный результат переменной для следующей итерации цикла.
В Python предусмотрен составной оператор присваивания для каждой арифметической операции:
y += 1 # добавить число и присвоить результат y -= 1 # отнять число и присвоить результат y *= 2 # умножить на число и присвоить результат y /= 3 # разделить на число и присвоить результат y // = 5 # разделить без остатка на число и присвоить результат y **= 2 # возвести в степень и присвоить результат y %= 3 # вернуть остаток от деления и присвоить результат
Составные операторы присваивания полезны в тех случаях, когда переменная должна увеличиваться или уменьшаться с помощью инкремента. А также когда необходимо автоматизировать некоторый процесс в создаваемой программе.
Сравнение двойной косой черты python с другими языками программирования
Каждый язык программирования решает целочисленное/целочисленное деление по-разному. Если мы попытаемся выполнить 5/2 в C++ или в Java, то получим следующий результат-
C++
#include
using namespace std;
int main()
{
cout<<5/2;
return 0;
}
Выход-
2
Java-
public class Division{
public static void main(String []args){
System.out.println(5/2);
}
}
Выход-
2
Как вы, должно быть, заметили, в отличие от python, здесь мы получаем 2.5 в качестве вывода. И если мы хотим получить наш результат в плавающих точках, нам нужно сделать href=”https://en.wikipedia.org/wiki/Divide”>разделите вот так – 5.0/2. href=”https://en.wikipedia.org/wiki/Divide”>разделите вот так – 5.0/2.
Оценка производительности
pympler
Потребление памяти в Python отдельная проблема, которой можно посвятить много времени, поэтому зачастую приходится следить за тем, чтобы python не сожрал всю оперативку. Для проверки памяти есть замечательный модуль pympler, который поможет не только посмотреть память, занимаемую объектом, но также поможет проследить за памятью, которую занимают отдельные классы или типы данных:
Проследим за изменением памяти, занимаемой классом A:
И в целом за памятью, занимаемой различными структурами
py-spy
Но знать распределение памяти зачастую недостаточно, так как программа может тормозить и не выполнять работу за ожидаемое время. В таком случае необходимо отследить, какие процессы сколько времени занимают.
В таком случае можно воспользоваться библиотекой py-spy, она позволяет без остановки программы проверить, сколько времени какие процессы в ней занимают. Установить библиотеку можно через pip install py-spy. Усложним код предыдущей программы, создадим дополнительный модуль sec.py:
модуль main.py:
Теперь через терминал достаточно прописать команду py-spy top — python main.py и вы будете получать информацию о времени работы каждого метода программы:
2 ответа
Лучший ответ
Согласованность .
Вам нужно будет следовать некоторым очень простым и, казалось бы, неуместным объяснениям, чтобы понять это.
В школе вы выучили деление с остатком. И вы сделали расчеты следующим образом:
Позже вы выучили деления на действительные числа:
До этого момента вы можете полагать, что и всегда дают один и тот же результат. Это ваше текущее понимание ситуации.
Однако посмотрите, что происходит в целочисленном делении: число за R циклически изменяется от 3, 2, 1 до 0, а затем перезапускается: 3, 2, 1, 0. Число перед R уменьшается с каждым 4-м шагом.
Итак, как это будет продолжаться?
В то же время деление действительных чисел дает нам:
Вот почему дает -1, а дает 0.
Ну, они служат различным целям: является частью вычисления целых чисел с остатками, а дает вам часть перед операции с действительным числом.
Вы решаете, что вы хотите вычислить, затем вы решаете, какой оператор использовать в Python, чтобы получить правильный результат.
Хороший вопрос. Продолжайте учиться.
61
Thomas Weller
12 Дек 2019 в 12:56
Я бы сказал, что ваше наблюдение о том, что эти 2 операции должны быть интуитивно схожими, ожидается, поскольку при положительных числах они ведут себя одинаково. Но если вы посмотрите на их происхождение (одно из математики, а другое — из информатики), тогда будет более понятно их различное поведение.
Вы можете посмотреть там концепции:
- Этажное деление или функция пола, применяемое к математическому разделению
- Тип преобразования / Тип литья
================================================== ================
I) Этажное деление или функция пола, применяемая к математическому разделу
Функция пола — очень хорошо зарекомендовавшая себя концепция математики.
Из mathworld.wolfram:
Таким образом, разделение по этажам — это не более, чем функция по этажам, применяемая к математическому разделению. Поведение очень ясное, «математически точное».
II) Преобразование типов / приведение типов
Из википедии:
В большинстве языков программирования приведение формы с плавающей точкой к целому числу применяется правилом округления (поэтому существует соглашение):
Округление к 0 — направленное округление к нулю (также известное как усечение)
Правило округления в соответствии с IEEE 754.
Итак, другими словами, причина различия между целочисленным делением и преобразованием с плавающей точкой в int в python является математической, вот некоторые мысли от Гвидо ван Россума (думаю, мне не нужно его представлять: D) (из блог История Python, статья «Почему Python Целочисленное деление этажей «)
4
rusu_ro1
7 Янв 2020 в 22:09
Реализация KNN в Python
Теперь, давайте попробуем реализовать концепцию KNN, чтобы решить проблему ниже регрессии.
Мы были предоставлены набором данных, который содержит исторические данные о количестве людей, которые решили арендовать велосипед в зависимости от различных условий окружающей среды.
Вы можете найти набор данных здесь .
Итак, давайте начнем!
1. Загрузите набор данных
Мы использовали использование Модуль пандас загрузить набор данных в среду, используя функция.
import pandas
BIKE = pandas.read_csv("Bike.csv")
2. Выберите правильные функции
Мы использовали методику корреляции регрессионного анализа для выбора важных переменных из набора данных.
corr_matrix = BIKE.loc.corr() print(corr_matrix)
Корреляционная матрица
temp atemp hum windspeed
temp 1.000000 0.991738 0.114191 -0.140169
atemp 0.991738 1.000000 0.126587 -0.166038
hum 0.114191 0.126587 1.000000 -0.204496
windspeed -0.140169 -0.166038 -0.204496 1.000000
Как «TEMP» и «ATEMP» очень коррелируют, мы бросаем «atemp» из набора данных.
BIKE = BIKE.drop(,axis=1)
3. Разделите набор данных
Мы использовали функцию reake_test_split () для разделения набора данных в 80% тренировках и набора данных на 20%.
#Separating the dependent and independent data variables into two data frames. from sklearn.model_selection import train_test_split X = bike.drop(,axis=1) Y = bike # Splitting the dataset into 80% training data and 20% testing data. X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=.20, random_state=0)
4. Определите метрики ошибок
Поскольку это проблема регрессии, мы определили Maпе в виде метрик ошибок, как показано ниже-
import numpy as np
def MAPE(Y_actual,Y_Predicted):
mape = np.mean(np.abs((Y_actual - Y_Predicted)/Y_actual))*100
return Mape
5. Создайте модель
Содержит метод реализации KNN, как показано ниже-
#Building the KNN Model on our dataset from sklearn.neighbors import KNeighborsRegressor KNN_model = KNeighborsRegressor(n_neighbors=3).fit(X_train,Y_train)
Кроме того, мы предсказываем данные тестирования, используя функцию прогнозирования ().
KNN_predict = KNN_model.predict(X_test) #Predictions on Testing data
6. Проверка точности!
Мы называем описанную выше функцию Mape для проверки ошибки неправильной классификации и судить о точности прогнозов модели.
# Using MAPE error metrics to check for the error rate and accuracy level
KNN_MAPE = MAPE(Y_test,KNN_predict)
Accuracy_KNN = 100 - KNN_MAPE
print("MAPE: ",KNN_MAPE)
print('Accuracy of KNN model: {:0.2f}%.'.format(Accuracy_KNN))
Оценка точности KNN-
MAPE: 17.443668778014253 Accuracy of KNN model: 82.56%.
Кубический корень
Само название функции намекает нам на то, что она не подходит для извлечения корня степени отличной от двойки. Поэтому для извлечения кубических корней, сначала необходимо вспомнить связь между степенями и корнями, которую продемонстрируем на корне квадратном:
Вышеуказанное соотношение несложно доказать и для других степеней вида .
В случае с квадратным или кубическим корнем эти операции действительно эквивалентны, но, вообще говоря, в математике извлечение корня и возведение в дробную степень имеют существенные отличия при рациональных степенях вида m/n, где m != 1. Формально, в дробно-рациональную степень можно возводить только положительные вещественные числа. В противном случае возникают проблемы:
Таким образом, извлечь кубический корень в Python можно следующим образом:
Или же:
Функция exp() — вычисление экспоненты
Функция вычисляет значение экспоненты, то есть e ^ x конкретного числа переданной десятичной точки.
Синтаксис:
decimal.Decimal(decimal-number).exp()
Пример:
import decimal as d
d.getcontext().prec = 5
#Intializing with an addition operation
val = d.Decimal(12.201) + d.Decimal(12.20)
#Calculating exponential of the decimal value
exp = val.exp()
#variable with no calculations
no_math = d.Decimal(1.131231)
print("Sum: ",val)
print("Exponential: ", exp)
print(no_math)
Выход:
Decimal Number: 24.401 3.9557E+10 1.131231000000000097571728474576957523822784423828125
Следует помнить, что значение точности применяется, когда вы выполняете математические операции с двумя десятичными знаками, а не когда вы напрямую инициируете переменную со значениями, как показано с переменной «no_math» выше.
Степень
Целочисленная
В целочисленную степень можно возводить положительные и отрицательные и числа:
И функция и оператор «**» умеют возводить комплексные числа:
Показатель степени может быть положительным, отрицательным и нулевым:
Результат не определён, когда 0 возводят в отрицательную степень:
Ошибка деления на ноль возникает из-за следующего свойства степени:
Рациональная
Возведение числа в рациональную степень напрямую связано с извлечением корня из этого числа отношением:
Если рациональный показатель отрицательный, а основание равно нулю, то Питон все ещё будет выдавать ошибку:
В случае, когда основание меньше нуля, числитель показателя нечётный, а знаменатель, напротив, чётный, результат получается комплексным. Но это свойство рациональных степеней учитывается только в функции
В остальном возведение в рациональную степень работает, как и для целочисленной:
Вещественная
В начале автор объявил, что возведение в степень – штука несложная. Так вот, для вещественных степеней это уже не совсем так. Идеи, заложенные в эту операцию, хоть и просты, но их много, и каждая из них достойна собственной статьи. Описать вкратце разложение в ряд Тейлора и численное интегрирование не получится. Это будет не справедливо, как по отношению к вам, так и к математике. Поэтому, выделим главное:
Python умеет возводить в вещественную степень даже вещественные числа (пусть и псевдо)
Сделать такое инструментами математики ой как непросто:
Связь с другими языками
pythonnet
Иногда возникает потребность запустить код, написанный на другом языке, через Python, например, в целях проверки работы какого-либо стороннего модуля или для оптимизации кода. Существует несколько библиотек, позволяющих сделать это, например, pythonnet позволяет запустить некоторую часть кода, написанную на C# в Python (pythonnet позволяет рассматривать множество элементов clr, как модули в python).
Создаем проект библиотеки классов C# в visual studio, создаем в неё нужный класс или методы (в случае примера класс, содержащий метод вычисления дискриминанта), создаем .dll и запускаем через pythonnet (более подробно тут):
Обращаемся к C# через Python
JPype
Для этих же целей существует библиотека, которая позволяет запустить Java код в Python. Эта библиотека называется — JPype. Рассмотрим пример работы библиотеки.
Для начала установим её pip install jpype1, далее создадим Java проект, который в будущем скомпилируем в .jar архив, в проекте необходимо создать пакет, в нём класс и прописать следующий код (код вычисляет объем цилиндра):
Теперь можно создать .jar решение проекта.
В python коде импортируем библиотеку jpype, запустим JVM и пропишем путь к созданному .jar архиву. Далее по аналогии с pythonnet импортируем необходимые пакеты и классы:
Таким образом, pythonnet и jpype — отличные решения для интеграции кода C# и Java в Python проект.
Встроенные структуры данных Python
Списки – создаются при помощи квадратных скобок . В списках находятся значения, которые можно изменять. Это могут быть любые значения: числа, символы, строки и т.д. Также можно создать список при помощи функции list( ).

Словари – формируются при помощи фигурных скобок { } или функцией dict( ). Являются изменяемым объектом и включают себя попарно набор ключей и значений.
Кортежи – инициализируются при помощи обычных скобок ( ), еще можно использовать функцию tuple( ). Их можно назвать неизменяемым списком. После создания кортежа нельзя изменять его значения.
Множество – создание происходит с использованием фигурных скобок, как и в случае со словарем или применив функцию set( ). Множество содержит элементы, которые не повторяются и находятся в случайном порядке. Пустое множество создать нельзя. Множество удобно применять для того, чтобы удалить повторяющиеся элементы.
Транспонирование матрицы
Транспонирование матрицы в основном включает в себя переворачивание матрицы по соответствующим диагоналям, т. е. Меняет местами строки и столбцы входной матрицы. Строки становятся столбцами и наоборот.
Например: давайте рассмотрим матрицу A с размерами 3 × 2, т.е. 3 строки и 2 столбца. После выполнения операции транспонирования размеры матрицы A будут 2 × 3, т.е. 2 строки и 3 столбца.
основном выполняет транспонирование входной матрицы и создает новую в результате операции транспонирования.
Пример:
import numpy
matA = numpy.array()
print("Original Matrix A:\n")
print(matA)
print('\nDimensions of the original MatrixA: ',matA.shape)
print("\nTranspose of Matrix A:\n ")
res = matA.T
print(res)
print('\nDimensions of the Matrix A after performing the Transpose Operation: ',res.shape)
Выход:
Original Matrix A: ] Dimensions of the original MatrixA: (2, 5) Transpose of Matrix A: ] Dimensions of the Matrix A after performing the Transpose Operation: (5, 2)
В приведенном выше фрагменте кода я создал матрицу размером 2 × 5, т.е. 2 строки и 5 столбцов.
После выполнения операции транспонирования размеры результирующей матрицы составляют 5 × 2, то есть 5 строк и 2 столбца.
Выполнение операции сложения в векторе
Ниже мы выполнили операцию сложения векторов над векторами. Операция сложения будет выполняться element-wise manner, т.е. поэлементно, и, кроме того, результирующий вектор будет иметь такую же длину, что и два аддитивных вектора.
Синтаксис:
vector + vector
Пример:
import numpy as np
lst1 =
lst2 =
vctr1 = np.array(lst1)
vctr2= np.array(lst2)
print("Vector created from a list 1:")
print(vctr1)
print("Vector created from a list 2:")
print(vctr2)
vctr_add = vctr1+vctr2
print("Addition of two vectors: ",vctr_add)
Вывод:
Vector created from a list 1: Vector created from a list 2: Addition of two vectors:
Математические операторы Python 3
Оператор – это символ, которая обозначает операцию. Например, в математике знак плюса или + – это оператор сложения.
Мы рассмотрим схожие операторы, которые перешли в Python из математики. Но другие операторы специфичны именно для программирования.
Ниже представлена таблица с кратким обзором математических операторов, доступных в Python.
| Операция | Возвращаемое значение |
| x + y | Сумма x и y. |
| x — y | Разность x и y. |
| -x | Изменение знака x. |
| +x | Тождественность x. |
| x * y | Произведение x и y. |
| x / y | Частное от деления x на y. |
| x // y | Частное от целочисленного деления x на y. |
| x % y | Остаток от деления x / y. |
| x ** y | x в степени y. |
Стилизация print
icecream
Для форматирования вывода существует одна удобная библиотека под названием icecream. Она помогает упростить написание логов или принтов для отладки. Рассмотрим пример её работы:
Чтобы подключить информацию о том, в каком месте программы происходит вывод, необходимо добавить всего лишь один аргумент в конфигурации модуля:
Это помогает более точно понять в каком месте происходит сбой в работе программы:
Также можно поменять префикс, который добавляется в начале строки, по дефолту он задан “ic|”. Удобно добавить время для вывода, чтобы видеть в какой момент времени и сколько занимал переход от одного принта к другому.
Если у вас уже имеются расставленные принты в коде, то легко можно переприсвоить print на ic:
Рассмотрим пример вывода более сложных структур, например, словарей:
Как видно на скриншоте, то вывод данных в таком формате читать гораздо легче, нежели обычный принт.
Также эта библиотека предоставляет возможность стилизовать вывод в зависимости от предоставляемых данных. Например, если есть необходимость дополнительно оформлять текст ошибки (Exception) или есть желание дополнительно выводить тип данных:
colorama
Еще одна полезная библиотека — colorama, она позволит раскрашивать текст в консоли. Её удобно использовать совместно с библиотекой icecream. Рассмотрим пару примеров:
Многопоточность (многозадачность)
multitasking
multitasking — очень удобная библиотека, которая позволяет только лишь при помощи обертки одним декоратором создавать асинхронные, неблокирующие методы. Эту библиотеку удобно использовать, когда возникает необходимость вызвать в отдельном потоке какой-либо неблокирующий метод, например, при обращении к БД или при ожидании какого-либо ответа от системы, но при этом не очень хочется городить кучу вызовов потоков и т.д..
Достаточно выполнить простую установку: pip install multitasking и далее оборачивать метод декоратором @task
И если удалить @multitasking.task, код выполнится последовательно:
Программа на Python с векторизацией и построением графиков
Вернемся к задаче, описывающей вертикальное положение \( y \) мяча после
подбрасывания. Предположим, что нас интересуют значения \( y \) в
каждую миллисекунду первой секунды полета. Это требует повторения
вычисления \( y = v_0 t — 0.5 g t^2 \) тысячу раз.
Также построим график зависимости \( y \) от \( t \) на отрезке
\( \). Построение такого графика на компьютере подразумевает
рисование прямых отрезков между точками кривой, поэтому нам
понадобится много точек, чтобы создать визуальный эффект гладкой
кривой. Тысячи точек, которые мы вычислим, нам будет достаточно для
этого.
Реализацию таких вычислений и построения графика может быть
реализовано следующим сценарием (ball_plot.py):
# -*- coding: utf-8 -*- from numpy import linspace import matplotlib.pyplot as plt v0 = 5 g = 9.81 t = linspace(, 1, 1001) y = v0*t - 0.5*g*t**2 plt.plot(t, y) plt.xlabel(u't (с)') plt.ylabel(u'y (м)') plt.show() def height(t): h = v0*t - 0.5*g*t**2 return h h = lambda t: v0*t - 0.5*g*t**2
Замечание
В нашем сценарии для символьных аргументов мы использовали префикс
(например, ), чтобы указать, что
символы содержатся в кодировке UTF8.
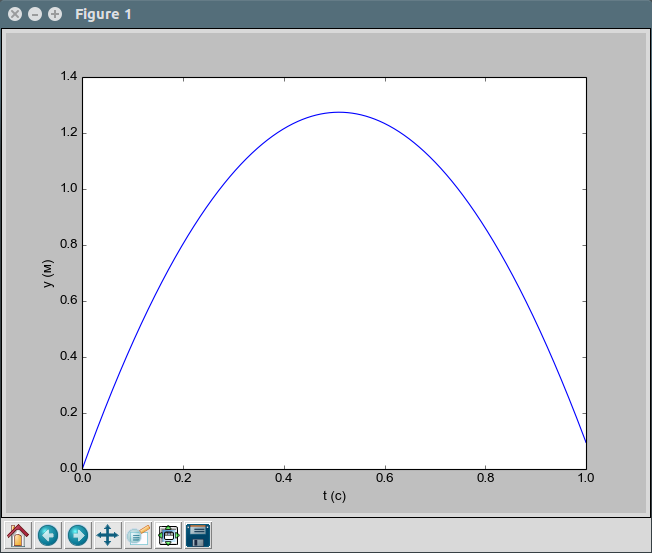
Данный сценарий строит график зависимости вертикального положения мяча
от времени (см. рис. :numref:`%s`). Отметим, что строки для
вычисления из сценария ball.py из раздела
мало изменены, но значение
вычисляется для тысячи точек.
Рассмотрим различия рассматриваемого сценария от предыдущих. Первое
отличие это строки, которые могли выглядеть следующим образом:
from numpy import * from matplotlib.pyplot import *
Мы видим, что является модулем Python. Этот модуль содержит
огромный функционал для математических вычислений, а модуль
реализует возможности для построения двумерных
графиков. Приведенные выше строки представляют быстрый способ загрузки
всего функционала, связанного с вычислениями и построением
графиков. Однако, фактически мы используем только несколько функций в
нашем сценарии: , , и
. Многие разработчики считают, что мы должны импортировать
только то, что нам нужно, а не весь возможный функционал:
from numpy import linspace from matplotlib.pyplot import plot, xlabel, ylabel
Другие предлагают способ импорта, когда используется префикс для
функций модуля
import numpy as np import matplotlib.pyplot as plt ... t = np.linspace(, 1, 1001) ... plt.plot(x,y)
Мы будем использовать все три способа. В нашем сценарии мы
использовали два из них.
from numpy import linspace import matplotlib.pyplot as plt
Рисунок 1: График, построенный с помощью нашего сценария.
Функция принимает три аргумента и, в общем случае,
вызывается следующим образом:
linspace(start, stop, n)
Функция генерирует равноотстоящих координат,
начинающихся со значения , и заканчивающихся
. Выражение создает 1001 координату
от 0 до 1 включительно. Математически это означает, что отрезок
\( \) разбивается на 1000 равных отрезков и значения координат
в этом случае вычисляются следующим образом: \( t_i = i/1000,\ i = 0, 1,
\ldots, 1000 \).
Функция возвращает объект класса ,
т.е. некоторый набор чисел (массив). При выполнении арифметических операций с
такими объектами, на самом деле эти операции осуществляются для каждого
элемента массива. В результате получается аналогичный массив из 1001
элемента, который сохраняется в переменную . Таким образом
также является массивом.
Такой подход вычисления нескольких чисел в одну строку называется
векторизацией. Этот способ очень удобен, так как сокращает не только
количество кода, но и время вычислений по сравнению с использованием
циклов или .
Команды для построения графиков достаточно просты:
1. означает построение графика зависимости от
2. помещает текст на оси .
3. помещает текст на оси .
Максимальные и минимальные
Десятичный модуль содержит следующие функции для вычисления минимального и максимального значений десятичной запятой.
- Функция min(): возвращает минимум двух десятичных значений.
- Функция max(): возвращает максимальное из двух десятичных значений.
#Syntax for min() function- decimal1.min(decimal2) #Syntax for max() function- decimal1.max(decimal2)
Пример:
import decimal as d
valx = d.Decimal(122.20)
valy = d.Decimal(123.01)
print("Value 1: ",valx)
print("Value 2: ",valy)
min_val = valx.min(valy)
print("The minimum of the two values: ",min_val)
max_val = valx.max(valy)
print("The maximum of the two values: ",max_val)
Выход:
Value 1: 122.2000000000000028421709430404007434844970703125 Value 2: 123.0100000000000051159076974727213382720947265625 The minimum of the two values: 122.2000000000000028421709430 The maximum of the two values: 123.0100000000000051159076975
Примеры решения задач
Возведение числа в степень с помощью цикла while
n = int(input()) # число
k = int(input()) # степень
i = 1 # текущая степень
result = 1
while i k:
result *= n
i += 1
print(result)
Сумма последовательности с помощью цикла while
n = int(input())
result =
i =
while i n:
result += i
i += 1
print(result)
Ввод последовательности чисел
i =
while True:
n = input()
if n == ‘end’:
print(‘Ввод закончен’)
print(‘Было введено’, i, ‘чисел’)
break
n = int(n)
i += 1
Сумма введенных чисел
i =
summa =
while True:
n = input()
if n == ‘end’:
print(‘Ввод закончен’)
print(‘Было введено’, i, ‘чисел’)
print(‘Их сумма равна’, summa)
break
n = int(n)
summa += n
i += 1
Программа на Python с переменными
Рассмотрим пример иллюстрирующий математическую модель описывающий
траекторию полета мяча в воздухе. Из второго закона Ньютона,
предполагая незначительное сопротивление воздуха, мы можем вывести
зависимость вертикального положения \( y \) мяча от времени
\( t \):
$$
\begin{equation*}
\tag{1}
y = v_0 t -0.5 g t^2
\end{equation*}
$$
где \( v_0 \) — начальная скорость, \( g \) — ускорение
свободного падения, значение которого положим равным \( 9.81 \) м/c \( ^2 \).
Сценарий
Рассмотрим сценарий на Python для вычисления по простой
формуле. Предположим, что сценарий у нас сохранен в виде текста в
файле ball.py
# -*- coding: utf-8 -*- # Программа для вычисления положения мяча при вертикальном движении v0 = 5 # Начальная скорость g = 9.81 # Ускорение свободного падения t = 0.6 # Время y = v0*t - 0.5*g*t**2
Разбор сценария
Сценарий на языке Python — это текстовый файл (в нашем случае
ball.py), содержащий некоторые
инструкции. Мы можем читать сценарий и понимать, что программа
способна делать, но сам сценарий не выполняет никаких действий на
компьютере, пока интерпретатор Python не прочитает текст сценария и не
преобразует его в некоторые действия.
Когда сценарий запущен в интерпретаторе Python, он разбирается и выполняется
построчно. Первые две строки
# -*- coding: utf-8 -*- # Программа для вычисления положения мяча при вертикальном движении
являются
комментариями*, т.е. как только встречается символ ,
интерпретатор Python воспринимает оставшуюся часть строки как
комментарий, пропускает ее и переходит к следующей строки.
Замечание
В первой строке указывается кодировка,
в которой сохранен файл сценария (в нашем случае *— это UTF8). Если в
сценарии не предполагается использование не ASCII символов, то первую
строку можно опустить. Однако, мы можем использовать
кириллический текст, поэтому в наших сценариях мы всегда будем
указывать кодировку.
Следующие 3 строки, интерпретируемые Pyhton:
v0 = 5 # Начальная скорость g = 9.81 # Ускорение свободного падения t = 0.6 # Время
В Python выражения вида известны как операторы
присваивания. Значение правой части, в нашем случае целое число
, становится объектом, а имя переменной слева *— именованной
ссылкой на этот объект. Всякий раз, когда мы запишем , Python
заменит ее целым значением . Выражение создает новое
имя для того же целого объекта со значением , а не копирует
объект.
Таким образом, прочитав эти строки интерпретатор Python знает три
переменных и их значения. Эти переменные используются
интерпретатором в следующей строке, фактически реализующей некоторую
формулу
y = v0*t - 0.5*g*t**2
В этой строке Python интерпретирует как оператор умножения, *—
вычитания, *— возведения в степень (естественно, и
интерпретируются как операторы сложения и деления соответственно). В
результате вычисляется значение по формуле в правой части выражения,
которое присваивается переменной с именем . Последняя строка
сценария
print y
выводит на печать значение переменной . Таким образом при запуске
сценария ball.by на экране будет выведено
число . В тексте сценария имеются также и пустые строки, которые
пропускаются интерпретатором Python. Они добавлены для лучшей
читабельности кода.
Запуск сценариев Python
Сценарии Python обычно имеют расширение , но это не является
необходимым. Как мы уже говорили, рассмотренный выше сценарий сохранен
в файле ball.py. Запустить его можно
следующей командой:
python ball.py
Такая команда явно указывает, что в качестве интерпретатора файла
должен использоваться Python. Также могут задаваться
аргументы командной строки, который загружается сценарием.
Команда должна запускаться в консольном окне
(терминал в Unix, Командная строка (Command Prompt) в MS Windows).
В случае, когда файлу установлено разрешение на выполнение (команда
) в ОС Unix (Linux), сценарий можно запускать
командой, сценарий можно запускать командой
./ball.py
В этом случае первая строка сценария должна содержать описание
интерпретатора:
#!/usr/bin/env python
В ОС MS Windows можно писать просто
ball.py
вместо , если расширение ассоциировано с
интерпретатором Python.
8 ответов
Лучший ответ
Делайте деление с плавающей точкой, затем конвертируйте в int. Никаких дополнительных модулей не требуется.
19
Tim
12 Ноя 2013 в 01:54
Вы также можете использовать десятичный модуль как часть стандартных библиотек python.
В частности, «оператор целочисленного деления // ведет себя аналогично, возвращая целочисленную часть истинного фактора (усеченную до нуля), а не его пол, чтобы сохранить обычную идентичность x == (x // y) * y + x % y: «
Также ознакомьтесь с , поскольку они есть несколько способов просмотра / округления вашей информации — потолок, вниз, пол, половина вниз, половина даже, половина вверх, вверх и 05 округления.
Десятичное число было написано как решение традиционной проблемы двоичной математики в мире, ожидающем десятичных решений
1
jjisnow
13 Авг 2017 в 21:57
По умолчанию деление целых чисел по Python возвращает слово (к отрицательной бесконечности) без возможности изменить это. Вы можете прочитать причину BDFL Почему.
Чтобы сделать округление вверх, вы должны использовать:
Чтобы выполнить усечение до нуля и сохранить целочисленное деление, используйте , если a или b отрицательны, и деление по умолчанию, если оба положительны.
Это будет делать целочисленное деление и всегда округлять до нуля:
Сноска
Интересно, что C99 заявляет, что по умолчанию используется округление до нуля:
Печать :
5
Community
23 Май 2017 в 12:00
Зачем изобретать велосипед, если есть отличная функция math.trunc ()?
jjisnow
15 Сен 2019 в 07:08
Что бы это ни стоило, мое любимое решение — это одно. Только целочисленная арифметика, одно деление и все остальное линейное время:
Это предполагает, что положителен, но в большинстве приложений, которые я видел, это правда. Если вам также нужно иметь дело с отрицательным , то функция становится немного более сложной:
Некоторые примеры выходов:
4
Mark Dickinson
19 Ноя 2013 в 18:42
Вбрасывая мою шляпу с несколькими альтернативными идеями:
Умножьте знак числа [abs (x) / x] на abs (x) / 2.
Выполните сложение, но если число меньше нуля, добавьте единицу, чтобы сместить его ближе к 0.
1
user764357user764357
12 Ноя 2013 в 03:48
Правильный код для этого, на мой взгляд, слишком неясен, чтобы писать как 1-строчный. Так что я бы поместил это в функцию, например:
Хорошие возможности: он работает для любого размера int, не вносит никаких корректировок в необработанный () результат, если в этом нет необходимости, только делает одно деление ( также делит под покрытиями), и не создает целых чисел больше, чем входные. Это может иметь или не иметь значения в вашей заявке; они становятся более важными (для скорости), если вы используете «большие» целые числа.
1
Tim Peters
12 Ноя 2013 в 02:37
Попробуй это. Работает только для чисел больше -1
1
Conor Patrick
12 Ноя 2013 в 01:55