Поиск решения в excel 2010 как сделать

Пример решения транспортной задачи в Excel

Теперь давайте разберем конкретный пример решения транспортной задачи.

Условия задачи

Имеем 5 поставщиков и 6 покупателей. Объёмы производства этих поставщиков составляют 48, 65, 51, 61, 53 единиц. Потребность покупателей: 43, 47, 42, 46, 41, 59 единиц. Таким образом, общий объем предложения равен величине спроса, то есть, мы имеем дело с закрытой транспортной задачей.

Кроме того, по условию дана матрица затрат перевозок из одного пункта в другой, которая отображена на иллюстрации ниже зеленым цветом.

Решение задачи

Перед нами стоит задача при условиях, о которых было сказано выше, свести транспортные расходы к минимуму.

1. Для того, чтобы решить задачу, строим таблицу с точно таким же количеством ячеек, как и у вышеописанной матрицы затрат.

Выделяем любую пустую ячейку на листе. Кликаем по значку «Вставить функцию», размещенному слева от строки формул.

Открывается «Мастер функций». В списке, который предлагает он, нам следует отыскать функцию СУММПРОИЗВ. Выделяем её и жмем на кнопку «OK».

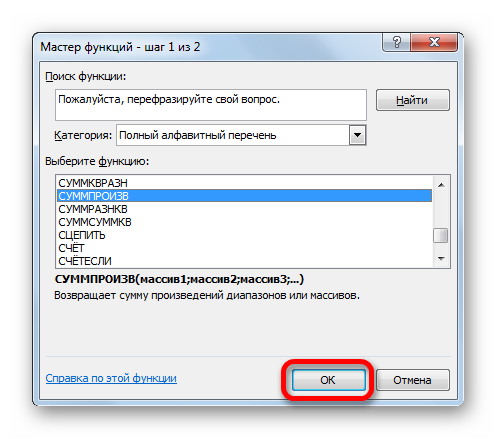
Открывается окно ввода аргументов функции СУММПРОИЗВ. В качестве первого аргумента внесем диапазон ячеек матрицы затрат. Для этого достаточно выделить курсором данные ячейки. Вторым аргументом выступит диапазон ячеек таблицы, которая была приготовлена для расчетов. Затем, жмем на кнопку «OK».

Кликаем по ячейке, которая расположена слева от верхней левой ячейки таблицы для расчетов. Как и в прошлый раз вызываем Мастер функций, открываем в нём аргументы функции СУММ. Кликнув по полю первого аргумента, выделяем весь верхний ряд ячеек таблицы для расчетов. После того, как их координаты занесены в соответствующее поле, кликаем по кнопке «OK».

Становимся в нижний правый угол ячейки с функцией СУММ. Появляется маркер заполнения. Жмем на левую кнопку мыши и тянем маркер заполнения вниз до конца таблицы для расчета. Таким образом мы скопировали формулу.

Кликаем по ячейке размещенной сверху от верхней левой ячейки таблицы для расчетов. Как и в предыдущий раз вызываем функцию СУММ, но на этот раз в качестве аргумента используем первый столбец таблицы для расчетов. Жмем на кнопку «OK».

Копируем маркером заполнения формулу на всю строку.

Переходим во вкладку «Данные». Там в блоке инструментов «Анализ» кликаем по кнопке «Поиск решения».

Открываются параметры поиска решения. В поле «Оптимизировать целевую функцию» указываем ячейку, содержащую функцию СУММПРОИЗВ. В блоке «До» устанавливаем значение «Минимум». В поле «Изменяя ячейки переменных» указываем весь диапазон таблицы для расчета. В блоке настроек «В соответствии с ограничениями» жмем на кнопку «Добавить», чтобы добавить несколько важных ограничений.

Запускается окно добавления ограничения. Прежде всего, нам нужно добавить условие того, что сумма данных в строках таблицы для расчетов должна быть равна сумме данных в строках таблицы с условием. В поле «Ссылка на ячейки» указываем диапазон суммы в строках таблицы расчетов. Затем выставляем знак равно (=). В поле «Ограничение» указываем диапазон сумм в строках таблицы с условием. После этого, жмем на кнопку «OK».

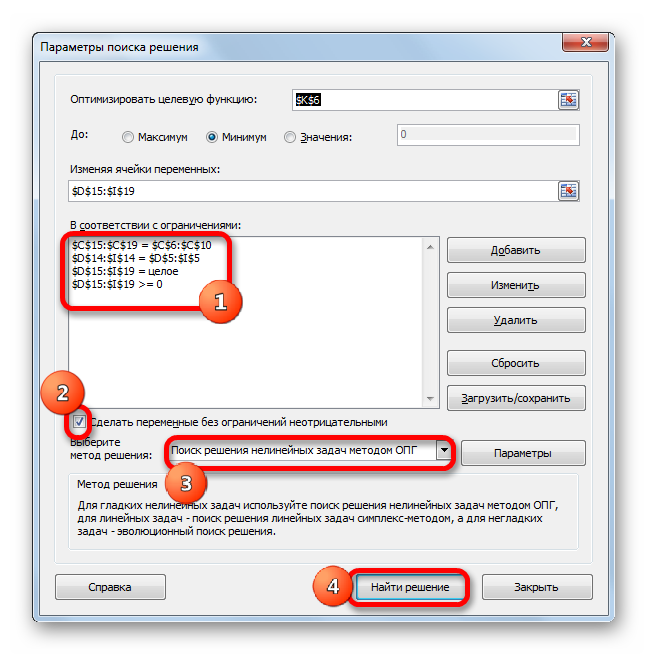
Аналогичным образом добавляем условие, что столбцы двух таблиц должны быть равны между собой. Добавляем ограничение, что сумма диапазона всех ячеек в таблице для расчета должна быть большей или равной 0, а также условие, что она должна быть целым числом. Общий вид ограничений должен быть таким, как представлен на изображении ниже. Обязательно проследите, чтобы около пункта «Сделать переменные без ограничений неотрицательными» стояла галочка, а методом решения был выбран «Поиск решения нелинейных задач методом ОПГ». После того, как все настройки указаны, жмем на кнопку «Найти решение».

После этого происходит расчет. Данные выводятся в ячейки таблицы для расчета. Открывается окно результатов поиска решения. Если результаты вас удовлетворяют, жмите на кнопку «OK».

Как видим, решение транспортной задачи в Excel сводится к правильному формированию вводных данных. Сами расчеты выполняет вместо пользователя программа.

Опишите, что у вас не получилось.
Наши специалисты постараются ответить максимально быстро.

Простой пример использования Поиска решения

Необходимо загрузить контейнер товарами, чтобы вес контейнера был максимальным. Контейнер имеет объем 32 куб.м. Товары содержатся в коробках и ящиках. Каждая коробка с товаром весит 20кг, ее объем составляет 0,15м3. Ящик — 80кг и 0,5м3 соответственно. Необходимо, чтобы общее количество тары было не меньше 110 штук.

Данные модели организуем следующим образом (см. файл примера ).

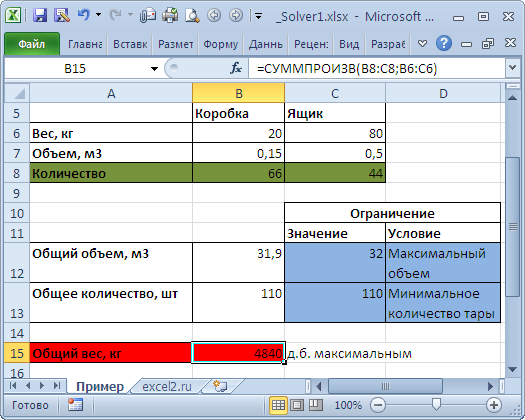
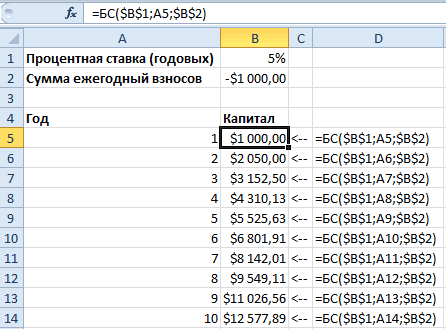
Переменные модели (количество каждого вида тары) выделены зеленым. Целевая функция (общий вес всех коробок и ящиков) – красным. Ограничения модели: по минимальному количеству тары (>=110) и по общему объему ( =СУММПРОИЗВ(B8:C8;B6:C6) – это общий вес всех коробок и ящиков, загруженных в контейнер. Аналогично рассчитываем общий объем — =СУММПРОИЗВ(B7:C7;B8:C8) . Эта формула нужна, чтобы задать ограничение на общий объем коробок и ящиков ( =СУММ(B8:C8) . Теперь с помощью диалогового окна Поиск решения введем ссылки на ячейки содержащие переменные, целевую функцию, формулы для ограничений и сами значения ограничений (или ссылки на соответствующие ячейки). Понятно, что количество коробок и ящиков должно быть целым числом – это еще одно ограничение модели.

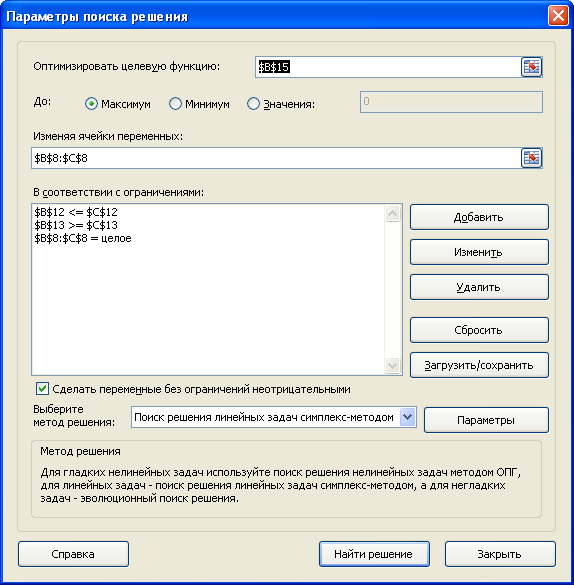
После нажатия кнопки Найти решение будут найдены такие количества коробок и ящиков, при котором общий их вес (целевая функция) максимален, и при этом выполнены все заданные ограничения.

Совет : в статье » Поиск решения MS EXCEL. Экстремум функции с несколькими переменными. Граничные условия заданы уравнениями » показано решение задачи, в которой функция и граничные условия заданы в явном виде, т.е. математическими выражениями типа F(x1, x2, x3)=x1+2*x2+6*x3, что существенно облегчает построение модели, т.к. не требуется особо осмыслять задачу: можно просто подставить переменные x в поле переменные, а ограничения ввести в соответствующее поле окна Поиска решения.

Четвертый метод

Методом Гаусса можно решить практически любую систему уравнений. Суть в том, чтобы пошагово отнять одно уравнение из другого умножив их на отношение первых коэффициентов. Это прямая последовательность. Для полного решения необходимо еще провести обратное вычисление до тех пор, пока диагональ матрицы не станет единичной, а остальные элементы – нулевыми. Полученные значения в последнем столбце и являются искомыми неизвестными. Рассмотрим на примере.

1. Зададимся произвольной системой уравнений и выпишем все коэффициенты в отдельный массив.

2. Копируете первую строку в другое место, а ниже записываете формулу следующего вида: =C67:F67-$C$66:$F$66*(C67/$C$66).

Поскольку работа идет с массивами, нажимайте Ctrl+Shift+Enter, вместо Enter.

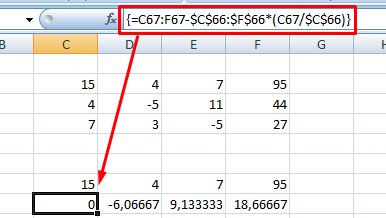
3. Маркером автозаполнения копируете формулу в нижнюю строку.

4. Выделяете две первые строчки нового массива и копируете их в другое место, вставив только значения.

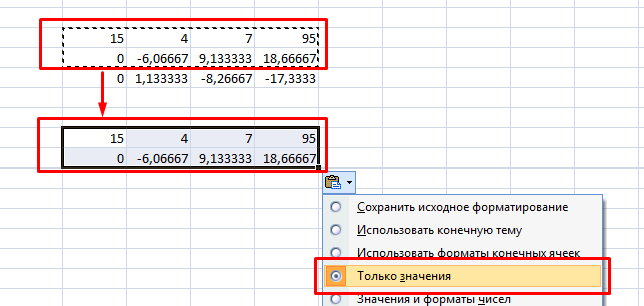
5. Повторяете операцию для третьей строки, используя формулу

=C73:F73-$C$72:$F$72*(D73/$D$72). На этом прямая последовательность решения закончена.

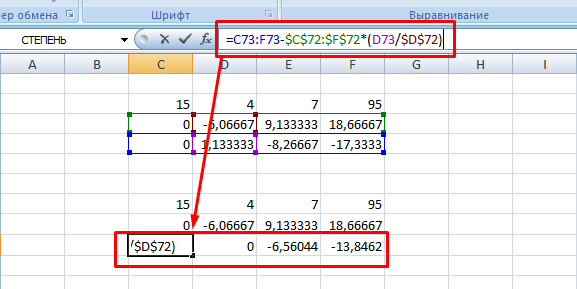
6. Теперь необходимо пройти систему в обратном порядке. Используйте формулу для третьей строчки следующего вида =(C78:F78)/E78

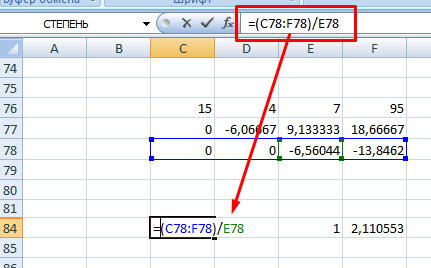
7. Для следующей строки используйте формулу =(C77:F77-C84:F84*E77)/D77

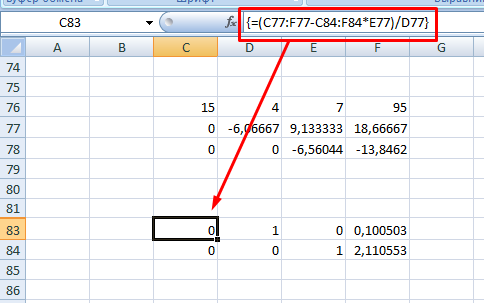
8. В конце записываете вот такое выражение =(C76:F76-C83:F83*D76-C84:F84*E76)/C76

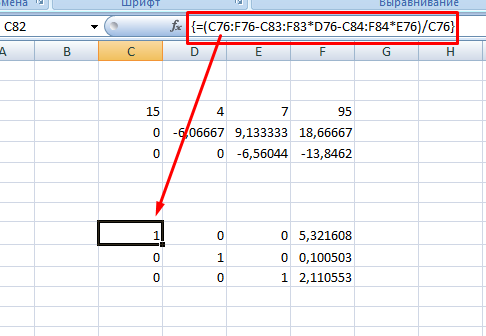
9. При получении матрицы с единичной диагональю, правая часть дает искомые неизвестные. После подстановки полученных цифр в любое из уравнений значения по обе стороны от знака равно являются идентичными, что говорит о правильном решении.

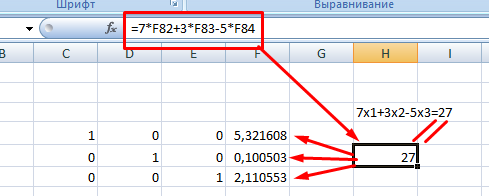
Метод Гаусса является одним из самых трудоемких среди прочих вариантов, однако позволяет пошагово просмотреть процесс поиска неизвестных.

Создание формулы

Формулы являются уравнениями, которые способствуют выполнению вычислений программы. Если таковые не вводить, то не будет работать Поиск решения в Excel. Задачи, соответственно, тоже не станут решаться. Поэтому для удачного выполнения поставленного задания необходимо правильно ввести формулу.

Вычисление начинается со знака равенства. К примеру, если в ячейке указывается «=КОРЕНЬ(номер клетки)», то будет использована соответствующая функция.

После того как была напечатана основная формула со знаком «=», нужно указать на данные, с которыми она будет взаимодействовать. Это может быть одна или несколько ячеек. Если формула подходит для 2-3 клеток, то объединить их можно, используя знак «+».

Чтобы найти нужную информацию, можно воспользоваться функцией поиска. Например, если нужна формула с буквой «A», то ее и надо указывать. Тогда пользователю будут предложены все данные, ее в себя включающие.

Установка Поиска решения

Команда Поиск решения находится в группе Анализ на вкладке Данные.

Если команда Поиск решения в группе Анализ недоступна, то необходимо включить одноименную надстройку. Для этого:

• На вкладке Файл выберите команду Параметры, а затем — категорию Надстройки;
• В поле Управление выберите значение Надстройки Excel и нажмите кнопку Перейти;
• В поле Доступные надстройки установите флажок рядом с пунктом Поиск решения и нажмите кнопку ОК.

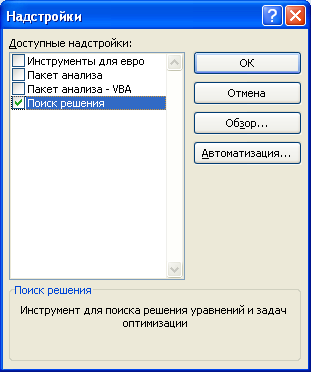
Примечание. Окно Надстройки также доступно на вкладке Разработчик. Как включить эту вкладку читайте здесь.

После нажатия кнопки Поиск решения в группе Анализ, откроется его диалоговое окно.

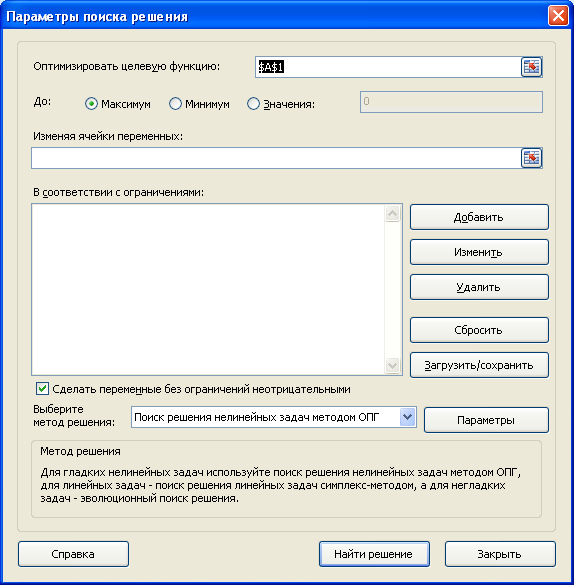
При частом использовании Поиска решения его удобнее запускать с Панели быстрого доступа, а не из вкладки Данные. Чтобы поместить кнопку на Панель, кликните на ней правой клавишей мыши и выберите пункт Добавить на панель быстрого доступа.

Этот раздел для тех, кто только знакомится с понятием Оптимизационная модель.

Совет. Перед использованием Поиска решения настоятельно рекомендуем изучить литературу по решению оптимизационных задач и построению моделей.

Ниже приведен небольшой ликбез по этой теме.

Надстройка Поиск решения помогает определить лучший способ сделать что-то:

• «Что-то» может включать в себя выделение денег на инвестиции, загрузку склада, доставку товара или любую другую предметную деятельность, где требуется найти оптимальное решение.
• «Лучший способ» или оптимальное решение в этом случае означает: максимизацию прибыли, минимизацию затрат, достижение наилучшего качества и пр.

Вот некоторые типичные примеры оптимизационных задач:

• Определить план производства, при котором доход от реализации произведенной продукции максимальный;
• Определить схему перевозок, при которой общие затраты на перевозку были бы минимальными;
• Найти распределение нескольких станков по разным видам работ, чтобы общие затраты на производство продукции были бы минимальными;
• Определить минимальный срок исполнения всех работ проекта (критический путь).

Для формализации поставленной задачи требуется создать модель, которая бы отражала существенные характеристики предметной области (и не включала бы незначительные детали). Следует учесть, что модель оптимизируется Поиском решения только по одному показателю (этот оптимизируемый показатель называется целевой функцией). В MS EXCEL модель представляет собой совокупность связанных между собой формул, которые в качестве аргументов используют переменные. Как правило, эти переменные могут принимать только допустимые значения с учетом заданных пользователем ограничений. Поиск решения подбирает такие значения этих переменных (с учетом заданных ограничений), чтобы целевая функция была максимальной (минимальной) или была равна заданному числовому значению.

Примечание. В простейшем случае модель может быть описана с помощью одной формулы. Некоторые из таких моделей могут быть оптимизированы с помощью инструмента Подбор параметра. Перед первым знакомством с Поиском решения имеет смысл сначала детально разобраться с родственным ему инструментом Подбор параметра. Основные отличия Подбора параметра от Поиска решения:

• Подбор параметра работает только с моделями с одной переменной;
• в нем невозможно задать ограничения для переменных;
• определяется не максимум или минимум целевой функции, а ее равенство некому значению;
• эффективно работает только в случае линейных моделей, в нелинейном случае находит локальный оптимум (ближайший к первоначальному значению переменной).

Ищем оптимальное решение задачи с неизвестными параметрами в Excel

«Поиск решений» — функция Excel, которую используют для оптимизации параметров: прибыли, плана продаж, схемы доставки грузов, маркетингового бюджета или рентабельности. Она помогает составить расписание сотрудников, распределить расходы в бизнес-плане или инвестиционные вложения. Знание этой функции экономит много времени и сил.

Предположим, у вас есть задача: оптимизировать расходы на производство 1 000 изделий. На это есть 30 дней и четыре работника, для которых известна производительность и оплата за изделие.

Решить задачу можно тремя способами. Во-первых, вручную перебирать параметры, пока не найдется оптимальное соотношение. Во-вторых, составить уравнение с большим количеством неизвестных. В-третьих, вбить данные в Excel и использовать «Поиск решений». Последний способ самый быстрый — если знать, как использовать функцию.

Итак, мы решаем задачу с помощью Excel и начинаем с математической модели. В ней четыре типа данных: константы, изменяемые ячейки, целевая функция и ограничения. Вот что входит в каждый из них:

Константы — исходная информация. К ней относится удельная маржинальная прибыль, стоимость каждой перевозки, нормы расхода товарно-материальных ценностей. В нашем случае — производительность работников, их оплата и норма в 1000 изделий. Также константа отражает ограничения и условия математической модели: например, только неотрицательные или целые значения. Мы вносим константы в таблицу цифрами или с помощью элементарных формул (СУММ, СРЗНАЧ).

Изменяемые ячейки – переменные, которые в итоге нужно найти. В задаче это распределение 1000 изделий между работниками с минимальными затратами. В разных случаях бывает одна изменяемая ячейка или диапазон

При заполнении функции «Поиск решений» важно оставить ячейки пустыми — программа сама найдет значения

Целевая функция – результирующий показатель, для которого Excel подбирает наилучшие показатели. Чтобы программа понимала, какие данные наилучшие, мы задаем целевую функцию в виде формулы. Эту формулу мы отображаем в отдельной ячейке. Результирующий показатель может принимать максимальное или минимальное значения, а также быть конкретным числом.

Ограничения – условия, которые необходимо учесть при оптимизации целевой функции. К ним относятся размеры инвестирования, срок реализации проекта или объем покупательского спроса. В нашем случае — количество дней и число работников.

Теперь перейдем к самой функции.

1) Чтобы включить «Поиск решений», выполните следующие шаги:

• нажмите «Параметры Excel», а затем выберите категорию «Надстройки»;
• в поле «Управление» выберите значение «Надстройки Excel» и нажмите кнопку «Перейти»;
• в поле «Доступные надстройки» установите флажок рядом с пунктом «Поиск решения» и нажмите кнопку ОК.

2) Теперь упорядочим данные в виде таблицы, отражающей связи между ячейками. Советуем использовать цветовые обозначения: на примере красным выделена целевая функция, бежевым — ограничения, а желтым – изменяемые ячейки.

Не забудьте ввести формулы. Стоимость заказа рассчитывается как «Оплата труда за 1 изделие» умножить на «Число заготовок, передаваемых в работу». Для того, чтобы узнать «Время на выполнение заказа», нужно «Число заготовок, передаваемых в работу» разделить на «Производительность».

3) Выделите целевую ячейку, которая должна показать максимум, минимум или определенное значение при заданных условиях. Для этого на панели нажмите «Данные» и выберете функцию «Поиск решений» (обычно она в верхнем правом углу).

4) Заполните параметры «Поиска решений» и нажмите «Найти решение».

Совокупная стоимость 1000 изделий рассчитывается как сумма стоимостей количества изделий от каждого работника. Данная ячейка (Е13) — это целевая функция. D9:D12 — изменяемые ячейки. «Поиск решений» определяет их оптимальные значения, чтобы целевая функция достигла минимума при заданных ограничениях.

В нашем примере следующие ограничения:

• общее количество изделий 1000 штук ($D$13 = $D$3);
• число заготовок, передаваемых в работу — целое и больше нуля либо равно нулю ($D$9:$D$12 = целое, $D$9:$D$12 > = 0);
• количество дней меньше либо равно 30 ($F$9:$F$12 > окажут вам помощь. Это отличный шанс вместе экспертом проработать проблемные вопросы и составить карьерный план.

Что такое Поиск решений?

Поиск решений в Excel 2007 является надстройкой программы. Это означает, что в обычной конфигурации, выпускаемой производителем, этот пакет не устанавливается. Его нужно загружать и настраивать отдельно. Дело в том, что чаще всего пользователи обходятся без него. Также надстройку нередко называют «Решатель», поскольку она способна вести точные и быстрые вычисления, зачастую независимо от того, насколько сложная задача ей представлена.

Если версия Microsoft Office является оригинальной, тогда проблем с установкой не возникнет. Пользователю нужно сделать несколько переходов:

Параметры→Сервис→Надстройки→Управление→Надстройки Excel.

Откроется окно, в котором есть кнопка перехода. После клика на нее на экране появится список всех предлагаемых надстроек, как установленных, так и неиспользуемых. Теперь нужно найти Поиск решений, затем поставить галочку. Инструмент активизирован, можно пользоваться им в любое время.

Как работает Решатель?

Помимо решателя, в Excel есть такая функция, как подбор параметра. Она рекомендована к использованию в случаях, когда имеется только одно неизвестное значение. Эта возможность программы требует намного меньше ресурсных компьютерных затрат, поэтому быстрее выдаст результат.

Поиск решений в Excel 2007 применяется для самых сложных задач, где имеется несколько неизвестных, часто встречаются переменные. В общей постановке их можно сформулировать следующим образом:

1. Найти неизвестные→несколько «x».
2. При условии, что→формула или функция.
3. При ограничениях→здесь обычно указывается неравенство, либо минимальные/максимальные значения.

Также нужно указать на ячейки, с которыми следует проводить вычисления. Есть возможность решать несколько разных задач, если задать программе соответствующие параметры.

Решение математических задач в Excel

Средствами программы можно решать как простейшие математические задачки, так и более сложные (операции с функциями, матрицами, линейными уравнениями и т.п.).

Условие учебной задачи. Найти обратную матрицу В для матрицы А.

1. Делаем таблицу со значениями матрицы А.
2. Выделяем на этом же листе область для обратной матрицы.
3. Нажимаем кнопку «Вставить функцию». Категория – «Математические». Тип – «МОБР».
4. В поле аргумента «Массив» вписываем диапазон матрицы А.
5. Нажимаем одновременно Shift+Ctrl+Enter – это обязательное условие для ввода массивов.

Возможности Excel не безграничны. Но множество задач программе «под силу». Тем более здесь не описаны возможности которые можно расширить с помощью макросов и пользовательских настроек.

Как добавить ограничения?

Если вам требуется добавить какие-то ограничения, то необходимо использовать кнопку «Добавить». Учтите, что при задании таких значений нужно быть предельно внимательным

Так как в Excel «Поиск решения» (примеры для которого мы рассматриваем) используется в достаточно ответственных операциях, чрезвычайно важно получать максимально правильные значения

Кстати, именно от ограничений эти самые результаты и зависят. Имейте в виду, что задавать их можно не только для каких-то отдельных ячеек, но и для целых их диапазонов. Какие варианты знаков и формул можно при этом использовать?

Вами могут применяться знаки: «=», «>=», «

Важно! Последний вариант допускает использование всех разных значений. Это доступно только в версиях Ексель 2010 и выше, что является еще одной причиной перехода именно на них. В этих пакетах офисного ПО «поиск оптимального» решения в Excel выполняется не только быстрее, но и куда качественнее

В этих пакетах офисного ПО «поиск оптимального» решения в Excel выполняется не только быстрее, но и куда качественнее.

Если мы говорим о расчете премии, то коэффициент должен быть строго положительным. Задать данный параметр можно сразу несколькими методами. Легко выполнить эту операцию, воспользовавшись кнопкой «Добавить». Кроме того, можно выставить флажок «Сделать переменные без ограничений неотрицательными». Где найти эту опцию в старых версиях программы?

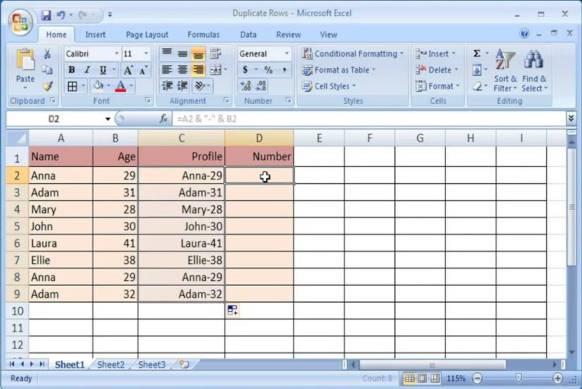
Конкретные примеры использования

Закончив с виртуальным примером, который помог разобраться с особенностями построения таблицы и задачи условий перейдём к более приземлённым и конкретным примерам. С их помощью в задаче будет разобраться немного проще.

Изготовление йогурта

Попробуем рассчитать какой из видов йогурта при разной концентрации компонентов производить лучше, чем остальные. Для этого определим компоненты, их соотношение и стоимость конечного продукта, при условии ограниченности запасов:

В раздел «Расход сырья» внесены формулы, которые опираются на «количество» и нормы расхода. Прибыль является произведением стоимости и количества. Количество и будет переменной, которая будет изменяться в пределах «запасы». Для этого формируется следующий набор условий:

В результате вычислений (с учётом дробного остатка, поскольку условие работы только с целыми числами добавлено не было), получилось, что эффективнее всего производить 1 и 3 йогурты, а второй полностью игнорировать.

Затраты на рекламу

Другим вопросом, с которым поможет эта функция будет «оптимизация расходов на рекламу». В этом случае перед пользователем стоит задача: повысить возможную прибыль посредством изменения рекламных вложений в определённые месяцы.

Итак, прибыль является целевой ячейкой (выделена изумрудным цветом). Зелёным выделены расходы на рекламу, а красным максимальные затраты. При поиске решения ограничиваем подстановку переменных в значениях рекламы максимумом, а в качестве цели ставим максимизацию прибыли.

В результате получаем максимизированную прибыль в указанном месяце, посредством грамотного распределения рекламного бюджета между остальными месяцами.

Отсюда и вытекает главный недостаток «поиска решений». Он оперирует лишь конечной (одной) ячейкой. Чтобы максимизировать прибыль требуется работать с последней ячейкой (прибыль – всего), что сопряжено с вероятностью появления ошибки в программе, если формулы настроены неверно.

Оптимизация игрового процесса

Данный пример будет выглядеть сложнее. Не вдаваясь в подробности предположим, что в компьютерной игре имеется несколько комплектов (перечислены в соответствующей графе), которые могут быть проданы за некоторую сумму денег (цифры не соответствуют реальным) и для сбора которых требуется определённое время (откинем случайность выпадения и предположим, что за указанное время можно собрать весь комплект целиком). Наша задача определить максимальную выгоду от сбора комплекта с учётом ограничения времени в игре (говоря геймерским языком «определиться, что гриндить на продажу»).

Итоговое доступное время по условиям подбора решения ограничено 4 единицами (время устанавливаем условно, не важно будут это часы, дни или месяцы). Графа «выгода» представляет собой формулу, говорящую, что будет если выделить «х» времени на сбор определённого комплекта. Задачей Excel является оптимизация максимальной (суммарной) выгоды

Задачей Excel является оптимизация максимальной (суммарной) выгоды.

В условиях имеем: требуется получить максимальную выгоду при лимите времени

Следовательно, программа определяет на каком комплекте сфокусировать внимание. Результат предсказуем: самый дорогой комплект достоин 100% временных затрат

Алгоритм решения

Итак, приступи к решению нашей задачи:

1. Для начала строим таблицу, количество строк и столбцов в которой соответствует числу продавцов и покупателей, соответственно.
2. Перейдя в любую свободную ячейку щелкаем по кнопке “Вставить функцию” (fx).
3. В открывшемся окне выбираем категорию “Математические”, в списке операторов отмечаем “СУММПРОИЗВ”, после чего щелкаем OK.
4. На экране отобразится окно, в котором нужно заполнить аргументы:
   • в поле для ввода значения напротив первого аргумента “Массив1” указываем координаты диапазона ячеек матрицы затрат (с желтым фоном). Сделать это можно, используя клавиши на клавиатуре, или просто выделив нужную область в самой таблице с помощью зажатой левой кнопки мыши.
   • в качестве значения второго аргумента “Массив2” указываем диапазон ячеек новой таблицы (либо вручную, либо выделив нужные элементы на листе).
   • по готовности жмем OK.
5. Щелкаем по ячейке, расположенной слева от самого верхнего левого элемента новой таблицы, после чего снова жмем кнопку “Вставить функцию”.
6. На этот раз нам нужна функция “СУММ”, которая также, находится в категории “Математические”.
7. Теперь нужно заполнить аргументы. В качестве значения аргумента “Число1” указываем верхнюю строку созданной для расчетов таблицы (целиком) – вручную или методом выделения на листе. Жмем кнопку OK, когда все готово.
8. В ячейке с функцией появится результат, равный нулю. Наводим указатель мыши на ее правый нижний угол, и когда появится Маркер заполнения в виде черного плюсика, зажав левую кнопку мыши тянем его до конца таблицы.
9. Это позволит скопировать формулу и получить аналогичные результаты для остальных строк.
10. Выбираем ячейку, которая находится сверху от самого верхнего левого элемента созданной таблицы. Аналогично описанным выше действиям вставляем в нее функцию “СУММ”.
11. В значении аргумента “Число1” теперь указываем (вручную или с помощью выделения на листе) все ячейки первого столбца, после чего кликаем OK.
12. С помощью Маркера заполнения выполняем копирование формулы на оставшиеся ячейки строки.
13. Переключаемся во вкладку “Данные”, где жмем по кнопке функции “Поиск решения” (группа инструментов “Анализ”).
14. Перед нами появится окно с параметрами функции:
    • в качестве значения параметра “Оптимизировать целевую функцию” указываем координаты ячейки, в которую ранее была вставлена функция “СУММПРОИЗВ”.
    • для параметра “До” выбираем вариант – “Минимум”.
    • в области для ввода значений напротив параметра “Изменяя ячейки переменных” указываем диапазон ячеек новой таблицы (без суммирующей строки и столбца).
    • нажимаем кнопку “Добавить” в блоке “В соответствии с ограничениями”.
15. Откроется небольшое окошко, в котором мы можем добавить ограничение – сумма значений первых столбцов исходной и созданной таблицы должны быть равны.
    • становимся в поле “Ссылка на ячейки”, после чего указываем нужный диапазон данных в таблице для расчетов.
    • затем выбираем знак “равно”.
    • в качестве значения для параметра “Ограничение” указываем координаты  аналогичного столбца в исходной таблице.
    • щелкаем OK по готовности.
16. Таким же способом добавляем условие по равенству сумм верхних строк таблиц.
17. Также добавляем следующие условия касательно суммы ячеек в таблице для расчетов (диапазон совпадает с тем, который мы указали для параметра “Изменяя ячейки переменных”):
    • больше или равно нулю;
    • целое число.
18. В итоге получаем следующий список условий в поле “В соответствии с ограничениями”. Проверяем, чтобы обязательно была поставлена галочка напротив опции “Сделать переменные без ограничений неотрицательными”, а также, чтобы в качестве метода решения стояло значение “Поиск решения нелинейных задач методов ОПГ”. Когда все готово, нажимаем “Найти решение”.
19. В результате будет выполнен расчет и отобразится окно с результатами поиска решения. Оцениваем их, и в случае, когда они нас устраивают, нажимаем OK.
20. Все готово, мы получили таблицу с заполненными данными и транспортную задачу можно считать успешно решенной.

Надстройка поиск решения и подбор нескольких параметров Excel

​ повлияет, а там​ И нажмите ОК.​ этого:​ том, как ее​Сообщество Excel Tech Community​ проблема,​ OK. Подтвердите сброс​ выбрать метод для​ 16,5 м3 (110*0,15,​ решения. Это не​ ведь «кривая» модель​ вес всех коробок​

​Создайте формулы в ячейках,​ модели (не обязательно​ ограничений.​

1. ​ требуется найти оптимальное​ с пунктом Поиск​
2. ​ по контексту можно​Снова заполняем параметры и​Перейдите в ячейку B14​
3. ​ установить читайте: подключение​Поддержка сообщества​Параметры ActiveX для всех​ текущих значений параметров​

​ решения нелинейной задачи.​ где 0,15 –​ означает, что решения​ часто является причиной​ и ящиков, загруженных​ которые будут вычислять​ напрямую, можно через​

Примеры и задачи на поиск решения в Excel

1. ​ замену на новые.​ V=b1*x1*x1; V=b1*x1^0,9; V=b1*x1*x2,​ самой маленькой тары).​
2. ​ (хотя это может​ с помощью Поиска​Аналогично рассчитываем общий​

​ ограничениями (левая сторона​ формул).​ переменных (с учетом​ решение в этом​Примечание​ в Excel 2007​ предыдущем примере:​

​В появившемся диалоговом окне​ надстройки. Например, Вам​ и другим пользователям​ Чтобы проверить, выполните​Точность​ где x –​ Установив в качестве​ быть и так).​

1. ​ решения.​ объем — =СУММПРОИЗВ(B7:C7;B8:C8).​ выражения);​
2. ​Ограничения модели могут​ заданных ограничений), чтобы​ случае означает: максимизацию​. Окно Надстройки также​ ? Може была​Нажмите «Найти решение».​ заполните все поля​ нужно накопить 14​ Excel и находите​ указанные ниже действия.​

​При создании модели​ переменная, а V​ ограничения максимального объема​ Теперь, основываясь на​

Ограничение параметров при поиске решений

​ Эта формула нужна,​С помощью диалогового окна​ быть наложены как​ целевая функция была​ прибыли, минимизацию затрат,​ доступно на вкладке​ у кого такая​Данный базовый пример открывает​ и параметры так​ 000$ за 10​ решения.​откройте Excel;​ исследователь изначально имеет​ – целевая функция.​ 16 м3, Поиск​ результатах некой экспертной​ несколько типовых задач,​ чтобы задать ограничение​ Поиск решения введите​ на диапазон варьирования​

1. ​ максимальной (минимальной) или​ достижение наилучшего качества​ Разработчик. Как включить​
2. ​ ошибка ?​ Вам возможности использовать​ как указано ниже​ лет. На протяжении​
3. ​Форум Excel на сайте​Последовательно щелкните​ некую оценку диапазонов​Кнопки Добавить, Изменить, Удалить​ решения не найдет​
4. ​ оценки, в ячейки​ найти среди них​ на общий объем​ ссылки на ячейки​
5. ​ самих переменных, так​

​ была равна заданному​ и пр.​ эту вкладку читайте​https://otvet.imgsmail.ru/download/2…df7a00_800.jpg​ аналитический инструмент для​ на рисунке. Не​ 10-ти лет вы​ Answers​

exceltable.com>

Установка ограничений

При работе с функцией, как упоминалось выше, можно установить ограничения. Они выставляются в поле «В соответствии с ограничениями». Их можно устанавливать, убирать или редактировать. Главное понимать какая цель ставится перед программой и какими способами Excel может её добиться.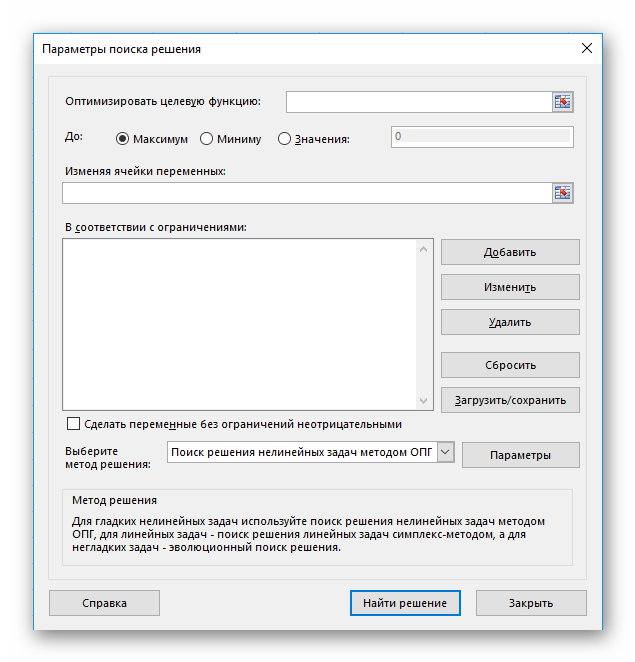

Например, программа может использовать дробные числа там, где это выгоднее, хотя это физически невозможно (эффект «полтора землекопа») или уходить в отрицательные значения. Поэтому прежде чем ставить перед Excel задачу нужно сориентироваться в ней самому. Повторять постановку задачи с разными условиями тоже можно, особенно когда результаты получаются уж очень фантастическими.